大家好,我是Weekoder!
今天的內容是快速冪!(實際上是為了講矩陣快速冪趕出來的嘻嘻
快速冪,顧名思義就是快速地計算出某個數的冪,形如 \(a^n\)。
為什麼普通的冪運算慢?假設要計算 \(a^n\),則需要拆分成 \(a\times a\times\cdots\times a\times a\),運算 \(n\) 次,複雜度為 \(O(n)\)。當 \(n\) 很大時,這個演算法明顯就不行了。那要怎麼最佳化呢?我們先來看一個簡單一點的例子:當 \(n\) 為 \(2\) 的冪時,可以怎麼做呢?假設 \(n\) 為 \(32\),可以這樣計算:
注意:\(a^x\times a^y=a^{x+y}\)。
可以發現,這樣只計算了 \(5\) 次,相比於樸素演算法的 \(32\) 次,將時間複雜度最佳化到了 \(O(\log n)\)。這其實是倍增的原理,相比於一個一個乘 \(a\),不如將 \(a\) 的數量翻倍乘。
那如果 \(n\) 不是 \(2\) 的冪呢?比如,\(n=105\) 的時候,該怎麼辦呢?雖然 \(105\) 不是 \(2\) 的冪,但是我們發現 \(105\) 可以拆分成 \(2\) 的冪之和,像這樣:
於是,我們可以把 \(a^{105}\) 拆分一下:
我們在剛剛提到過,計算 \(n\) 是 \(2\) 的冪的情況是很容易的,所以我們只需要將它們相乘即可。
這個問題的關鍵在於,怎樣將一個數拆分成 \(2\) 的冪之和?我們來看一下他們在二進位制下的樣子:
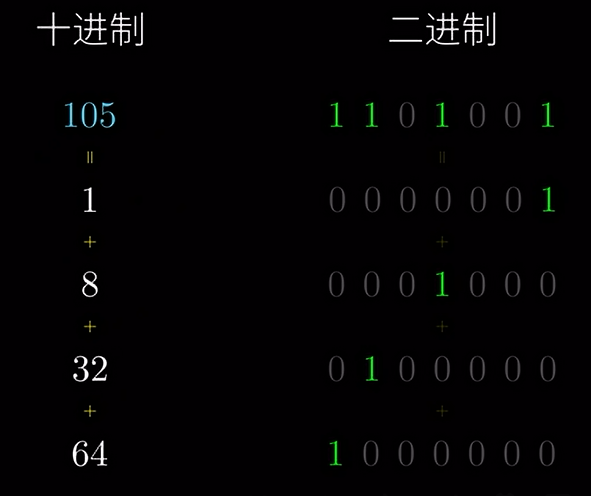
可以看到,\(105\) 的二進位制中有 \(4\) 個 \(1\),而 \(2\) 的冪的數都只有一個 \(1\),並且剛好和 \(105\) 的四個 \(1\) 位置一樣。所以,只要將 \(105\) 二進位制中的 \(1\) 拆開,就能得到 \(2\) 的冪的數字是哪些了。
而因為一個數 \(n\) 的二進位制最多隻有 \(\log n\) 位,所以時間複雜度為 \(O(\log n)\)。
就決定是你了!快速冪模板!
先上程式碼:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll expow(ll a, ll n, ll p) {
ll r = 1;
while (n) {
if (n & 1) r = r * a % p;
a = a * a % p, n >>= 1;
}
return r;
}
int main() {
ll a, b, p;
cin >> a >> b >> p;
cout << a << "^" << b << " mod " << p << "=" << expow(a, b, p);
return 0;
}
輸入和輸出就不用我講了,重點是 \(\text{expow}\) 函式。我把快速冪函式提取出來(先不取模):
typedef long long ll;
ll expow(ll a, ll n) {
ll r = 1;
while (n) {
if (n & 1) r *= a;
a *= a, n >>= 1;
}
return r;
}
比如計算 \(7^{105}\)。
首先,我們用一個 \(\color{yellow}\texttt{r}\color{#000000}\texttt{esult}\) 來儲存結果,初始時為 \(1\)。接著,有一個 \(\text{while}\) 迴圈,其實就是遍歷 \(n\) 在二進位制下的每一位。如果當前這一位是 \(1\),即 \(n\) 對 \(1\) 按位與的結果為 \(1\),則可以拆分,將 \(r\) 乘上 \(a\)。每過一位,\(a\) 就變為 \(a^2\),即模擬倍增的過程。然後還要將 \(n\) 除以 \(2\),用位運算表示就是右移一位,獲取下一位。最後返回結果 \(r\)。可以輔助圖片理解。
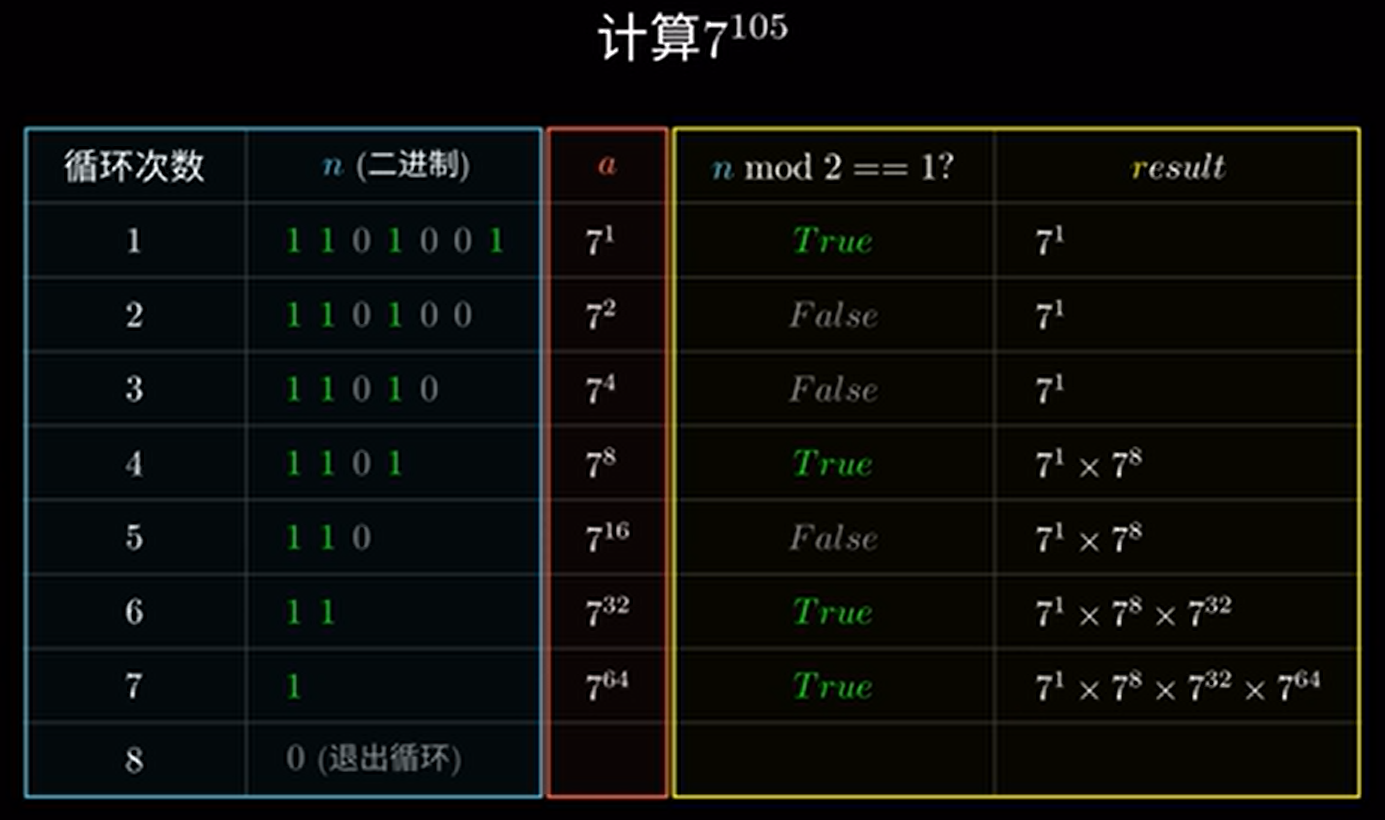
這樣就可以用 \(O(\log n)\) 的速度計算 \(a^n\) 了。
小擴充套件:冪取模
即計算 \(a^n \bmod p\)。
只需要在快速冪的模板裡稍微改動一下。在做乘法運算時,順帶取模就行了。
冪取模模板程式碼如下:
typedef long long ll;
ll expow(ll a, ll n, ll p) {
ll r = 1;
while (n) {
if (n & 1) r = r * a % p;
a = a * a % p, n >>= 1;
}
return r;
}
綜上所述,二進位制快速冪的核心就是這些了。當然,快速冪除了計算 \(a^n\) 以外,還有很多用處等著你去發現。