討論下一個token預測時，我們可能正在走進陷阱
机器之心發表於2024-03-25
自夏農在《通訊的數學原理》一書中提出「下一個 token 預測任務」之後，這一概念逐漸成為現代語言模型的核心部分。最近，圍繞下一個 token 預測的討論日趨激烈。然而，越來越多的人認為，以下一個 token 的預測為目標只能得到一個優秀的「即興表演藝術家」，並不能真正模擬人類思維。人類會在執行計劃之前在頭腦中進行細緻的想象、策劃和回溯。遺憾的是，這種策略並沒有明確地構建在當今語言模型的框架中。對此，部分學者如 LeCun，在其論文中已有所評判。在一篇論文中，來自蘇黎世聯邦理工學院的 Gregor Bachmann 和谷歌研究院的 Vaishnavh Nagarajan 對這個話題進行了深入分析，指出了當前爭論沒有關注到的本質問題：即沒有將訓練階段的 teacher forcing 模式和推理階段的自迴歸模式加以區分。- 論文標題：THE PITFALLS OF NEXT-TOKEN PREDICTION
- 論文地址：https://arxiv.org/pdf/2403.06963.pdf
- 專案地址：https://github.com/gregorbachmann/Next-Token-Failures
讀完此文，也許會讓你對下一個 token 預測的內涵有不一樣的理解。首先，讓我們對 「人們在進行語言表達或者完成某項任務時，並不是在做下一個 token 的預測」這個表述的含義進行分析。對於這種反對意見，可能馬上就會有 token 預測理論的支持者反駁到：不是每一個序列生成任務都可能是自迴歸的嗎？咋一看確實如此，每一個 token 序列的分佈都可以是一種鏈式規則，透過複雜的 token 預測模型進行模擬之後，這種規則就可以被捕捉到，即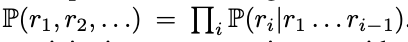 
。看上去似乎自迴歸學習方式與讓模型學習人類語言的目的是統一的。然而，這種簡單粗暴的想法並不妨礙我們認為 token 預測模型的規劃能力可能是很糟糕的。很重要的一點是，在這場爭論中人們並沒有仔細區分以下兩種型別的 token 預測方式：推理階段的自迴歸（模型將自己之前的輸出作為輸入）和訓練階段的 teacher-forcing（模型逐個對 token 進行預測，將所有之前的真值 token 作為輸入）。如果不能對這兩種情況做出區分，那當模型預測錯誤時，對複合誤差的分析往往只會將問題導向至推理過程，讓人們覺得這是模型執行方面的問題。但這是一種膚淺的認知，人們會覺得已經得到了一個近乎完美的 token 預測模型；也許，透過一個適當的後處理模型進行驗證和回溯後，可以在不產生複合錯誤的情況下就能得出正確的計劃。在明確問題之後，緊接著我們就需要想清楚一件事：我們能放心地認為基於 token 預測的學習方式（teacher-forcing）總是能學習到準確的 token 預測模型嗎？本文作者認為情況並非總是如此。以如下這個任務為例：如果希望模型在看到問題陳述 p = (p_1, p_2 ... ,) 後產生基本真實的響應 token (r_1, r_2, ...) 。teacher-forcing 在訓練模型生成 token r_i 時，不僅要提供問題陳述 p，還要部分基本事實 toekn r_1、...r_(i-1)。根據任務的不同，本文作者認為這可能會產生「捷徑」，即利用產生的基本事實答案來虛假地擬合未來的答案 token。這種作弊方式可以稱之為 「聰明的漢斯 」。接下來，當後面的 token 在這種作弊方法的作用下變得容易擬合時，相反，前面的答案 token（如 r_0、r_1 等）卻變得更難學習。這是因為它們不再附帶任何關於完整答案的監督資訊，因為部分監督資訊被「聰明的漢斯 」所剝奪。作者認為，這兩個缺陷會同時出現在 「前瞻性任務 」中：即需要在前一個 token 之前隱含地規劃後一個 token 的任務。在這類任務中，teacher-forcing 會導致 token 預測器的結果非常不準確，無法推廣到未知問題 p，甚至是獨立同分布下的取樣問題。根據經驗，本文作者證明了上述機制會導致在圖的路徑搜尋任務中會產生分佈上的問題。他們設計了一種能觀察到模型的任何錯誤，並都可以透過直接求解來解決的方式。作者觀察到 Transformer 和 Mamba 架構（一種結構化狀態空間模型）都失敗了。他們還發現，一種預測未來多個 token 的無教師訓練形式（在某些情況下）能夠規避這種失敗。因此，本文精心設計了一種易於學習的場景。在這種場景下會發現不是現有文獻中所批評的環節，如卷積、遞迴或自迴歸推理，而是訓練過程中的 token 預測環節出了問題。本文作者希望這些研究結果能夠啟發未來圍繞下一個 token 預測的討論，併為其奠定堅實的基礎。具體來說，作者認為，下一個 token 預測目標在上述這個簡單任務上的失敗，為其在更復雜任務（比如學習寫故事）上的應用前景蒙上了陰影。作者還希望，這個失敗的例子和無教師訓練方法所產生的正面結果，能夠激勵人們採用其他的訓練正規化。1. 本文整合了針對下一個 token 預測的現有批評意見，並將新的核心爭議點具體化；2. 本文指出，對下一個 token 預測的爭論不能混淆自迴歸推斷與 teacher-forcing，兩者導致的失敗的原因大相徑庭；3. 本文從概念上論證了在前瞻任務中，訓練過程中的下一個 token 預測（即 teacher-forcing）可能會產生有問題的學習機制，甚至產生分佈上的問題；4. 本文設計了一個最小前瞻任務。透過實證證明，儘管該任務很容易學習，但對於 Transformer 和 Mamba 架構來說，teacher-forcing 是失敗的；5. 本文發現，Monea et al. 為實現正交推理時間效率目標而提出的同時預測多個未來 token 的無教師訓練形式，有望在某些情況下規避這些訓練階段上的失敗。這進一步證明了下一個 token 預測的侷限性。本文的目標是更系統地分析並細緻區分下一個 token 預測的兩個階段：teacher forcing 和自迴歸。本文作者認為，現有的論證沒有完全分析出 token 預測模型無法規劃任務的全部原因。支持者對下一個 token 預測最熱的呼聲是：機率鏈規則總能推出一個能夠符合機率分佈的 token 預測。反對者認為，在自迴歸的每一步中都有可能出現微小的錯誤，而且一旦出錯就沒有明確的回溯機制來挽救模型。這樣一來，每個 token 中的錯誤機率，無論多麼微小，都會以指數級的速度越滾越大。反方抓住的是自迴歸在結構上的缺點。而正方對機率鏈規則的強調也只是抓住了自迴歸架構的表現力。這兩個論點都沒有解決一個問題，即利用下一個 token 預測進行的學習本身可能在學習如何規劃方面存在缺陷。從這個意義上說，本文作者認為現有的論證只捕捉到了問題的表象，即下一個 token 預測在規劃方面表現不佳。token 預測模型是否會在測試期間無法高精度地預測下一個 token？從數學上講，這意味著用 teacher forcing 目標訓練的模型在其訓練的分佈上誤差較大（從而打破了滾雪球模式的假設）。因此，任何後處理模型都無法找到一個能用的計劃。從概念上來說，這種失敗可能發生在「前瞻性任務」中，因為這些任務隱含地要求在更早的 token 之前提前計算未來的 token。為了更好地表述本文的論點所在，作者設計了一個圖的簡單尋路問題，深刻地抓住瞭解決前瞻性問題的核心本質。這項任務本身很容易解決，所以任何失誤都會非常直觀地體現出來。作者將這個例子視為其論點的模板，該論點覆蓋了 teacher forcing 下的前瞻性問題中的更一般、更困難的問題。這個論點就是，本文作者認為 teacher-forcing 可能會導致以下問題，尤其是在前瞻性問題中。- 問題 1：由於 teacher forcing 產生的「聰明的漢斯」作弊行為
儘管存在著一種機制可以從原始字首 p 中恢復每個 token r_i，但也可以有多種其他機制可以從 teacher forcing 的字首（p，r<i）中恢復 token r_i。這些機制可以更容易地被學習到，相應地就會抑制模型學習真正的機制。在訓練中解決了「聰明的漢斯」作弊行為後，模型被剝奪了一部分監督（尤其是對於較大的 i，r_i），這使得模型更難，甚至可能難以單獨從剩餘的 token 中學習真正的機制。本文透過圖路徑搜尋任務的實踐，演示了一種假設的故障模式。本文在 Transformer 和 Mamba 中進行了實驗，以證明這些問題對於 teacher-forced 模型來說是普遍的。具體來說，先確定 teacher-forced 模型能符合訓練資料，但在滿足資料分佈這個問題上存在不足。接下來，設計指標來量化上述兩種假設機制發生的程度。最後，設計了替代目標來干預和消除兩種故障模式中的每一種，以測試效能是否有所改善。本文對兩種模型家族進行了評估，以強調問題的出現與某種特定體系結構無關，而是源於下一個 token 預測這個設計目標。對於 Transformer，使用從頭開始的 GPT-Mini 和預訓練的 GPT-2 大模型。對於遞迴模型，使用從頭開始的 Mamba 模型。本文使用 AdamW 進行最佳化，直到達到完美的訓練精度。為了排除頓悟現象（grokking），本文對成本相對較低的模型進行了長達 500 個 epoch 的訓練。本文在圖 3 和表 2 中描述了不同拓撲路徑的星形圖的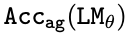
。可以觀察到，所有模型（即使經過預訓練）都很難準確地學習任務。如果模型一致地猜測認為 v_start≈1 /d，並由此在分佈上產生問題，則精度值能被嚴格限制。即使在訓練以擬合高達 200k 的量級到 100% 準確度的樣本量時也是如此，儘管訓練用的圖結構和測試用的圖結構具有相同的拓撲結構。接下來，本文定量地證明了這種明顯的問題是如何由上述兩個假設機制產生的。透過表 1 可以發現，為了擬合訓練資料，teacher-forced 模型利用了「聰明的漢斯」作弊方法。圖 3 和表 3 顯示了無教師模型的準確率。不幸的是，在大多數情況下，無教師的訓練目標對模型來說太難了，甚至無法擬合訓練資料，這可能是因為缺乏簡單有效的欺騙手段。然而，令人驚訝的是，在一些更容易的圖結構上，模型不僅適合於訓練資料，而且可以很好地泛化到測試資料。這個優秀的結果（即使在有限的環境中）驗證了兩個假設。首先，「聰明的漢斯」作弊方法確實是造成原有 teacher-forcing 模式失敗的原因之一。其次，值得注意的是，隨著作弊行為的消失，這些模型能夠擬合第一個節點，而這個節點曾經在 teacher-forcing 模式下是不可破譯的。綜上所述，本文所提出的假設可以說是得到了驗證了，即「聰明的漢斯」作弊方法抹去了對學習第一個 token 的至關重要的監督。