一. 大 O 表示法,分析時關注原則:
- 只關注迴圈次數最多的一段程式碼
- 加法原則:總複雜度等於量級最大那段程式碼複雜度
- 乘法原則:巢狀程式碼的複雜度等於巢狀程式碼內外複雜度的乘積
二.線性表結構
陣列
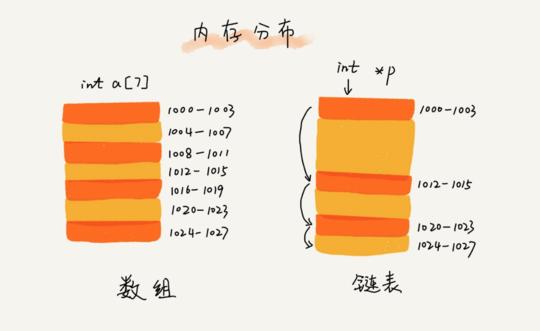
陣列(Array)是一種線性表資料結構,它用一組連續的記憶體空間,來儲存一組具有相同型別的資料。如果你學習過 C 語言,應該對這段定義很熟悉,但是在 PHP 這種動態語言中,因為陣列底層是通過雜湊表(後面我們會介紹這個資料結構)實現的,所以功能異常強大,這段常規的陣列定義在 PHP 中並不成立,PHP 的陣列可以儲存任何型別資料,如果與 Java 對比的話,PHP 陣列整合了 Java 的陣列、List、Set、Map 於一身,所以寫程式碼的效率比 Java 高了幾個量級
特性:拋開 PHP 或 JavaScript 這種動態語言,對於傳統的陣列,比如:C 語言和 Java 中的陣列,在使用之前都需要宣告陣列儲存資料的型別和陣列的大小,陣列的優點是可以通過下標值隨機訪問陣列內的任何元素,演算法複雜度是 O(1) ,非常高效,但是缺點是刪除/插入元素比較費勁。以刪除為例,需要在刪除某個元素後,將後續元素都往前移一位,如果是插入,則需要將插入位置後的元素都往後移,所以對陣列的插入/刪除而言,演算法複雜度是 O(n),當然了,這個針對 C/Java 這種語言而言,PHP 不受此約束,因為它不是傳統一樣的陣列。連結串列
與陣列不同,連結串列並不需要一塊連續的記憶體空間,它通過“指標”將一組零散的記憶體塊串聯起來使用,如圖:
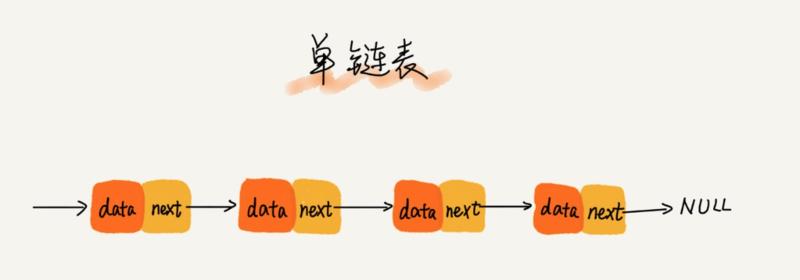
單向連結串列:有兩個節點比較特殊,分別是第一個節點和最後一個節點。我們通常把第一個節點叫做頭節點,把最後一個節點叫做尾節點。其中,頭節點用來記錄連結串列的基地址,有了它,可以遍歷得到整條連結串列。而尾節點特殊的地方是:指標不是指向下一個節點,而是指向 NULL,表示這是連結串列的最後一個節點。對單連結串列而言,理論上來說,插入和刪除節點的時間複雜是O(1),查詢節點的時間複雜度是 O(n)。如圖:
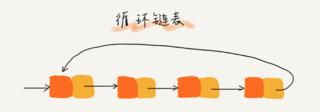
迴圈連結串列:迴圈連結串列和單連結串列的區別是尾節點執行的頭節點,從而頭尾相連,有點像貪吃蛇,可用於解決 [約瑟夫環] 問題,如圖:
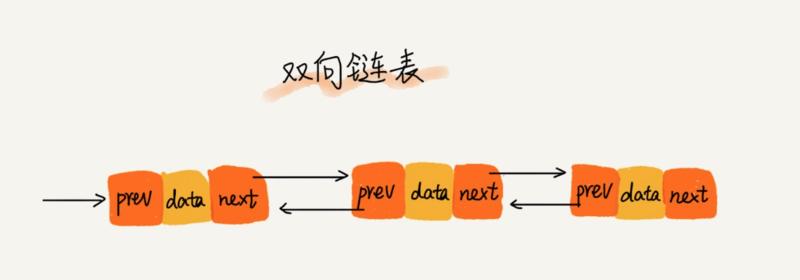
雙向連結串列: 與單連結串列的區別是雙向連結串列除了有一個指向下一個節點的指標外,還有一個用於指向上一個節點的指標,從而實現通過 O(1)複雜度找到上一個節點。正是因為這個節點,是的雙向連結串列的插入,刪除節點時比單連結串列更高效,雖然我們前面已經提到單連結串列插入,刪除時間複雜 O(1)了,但是這沒有考慮還只是針對插入,刪除本身而言。已刪除為例,刪除某個節點後,需要將其前驅節點的指標指向被刪除節點的下一個節點,這樣,我們還需要將獲取前驅節點,在單連結串列中獲取前驅節點的時間複雜度是O(n),所以綜合來看單連結串列的刪除,插入操作時間複雜度也是O(n),而雙向連結串列則不然,它有一個指標指向上一個節點,所以其插入和刪除時間複雜度才是正真的 O(1)。
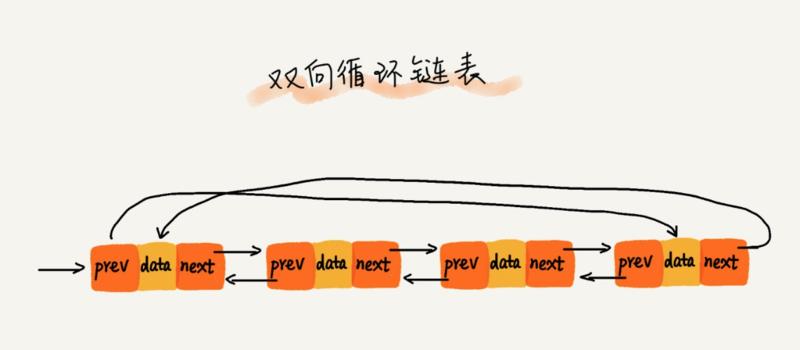
迴圈雙向連結串列: