連續子陣列的最大和
問題描述
輸入一個整型陣列,陣列中的一個或連續多個整陣列成一個子陣列。求所有子陣列的和的最大值。要求時間複雜度為O(n)。
示例:
輸入: nums = [-2,1,-3,4,-1,2,1,-5,4]
輸出:6
解釋:連續子陣列 [4,-1,2,1] 的和最大,為 6
分析問題
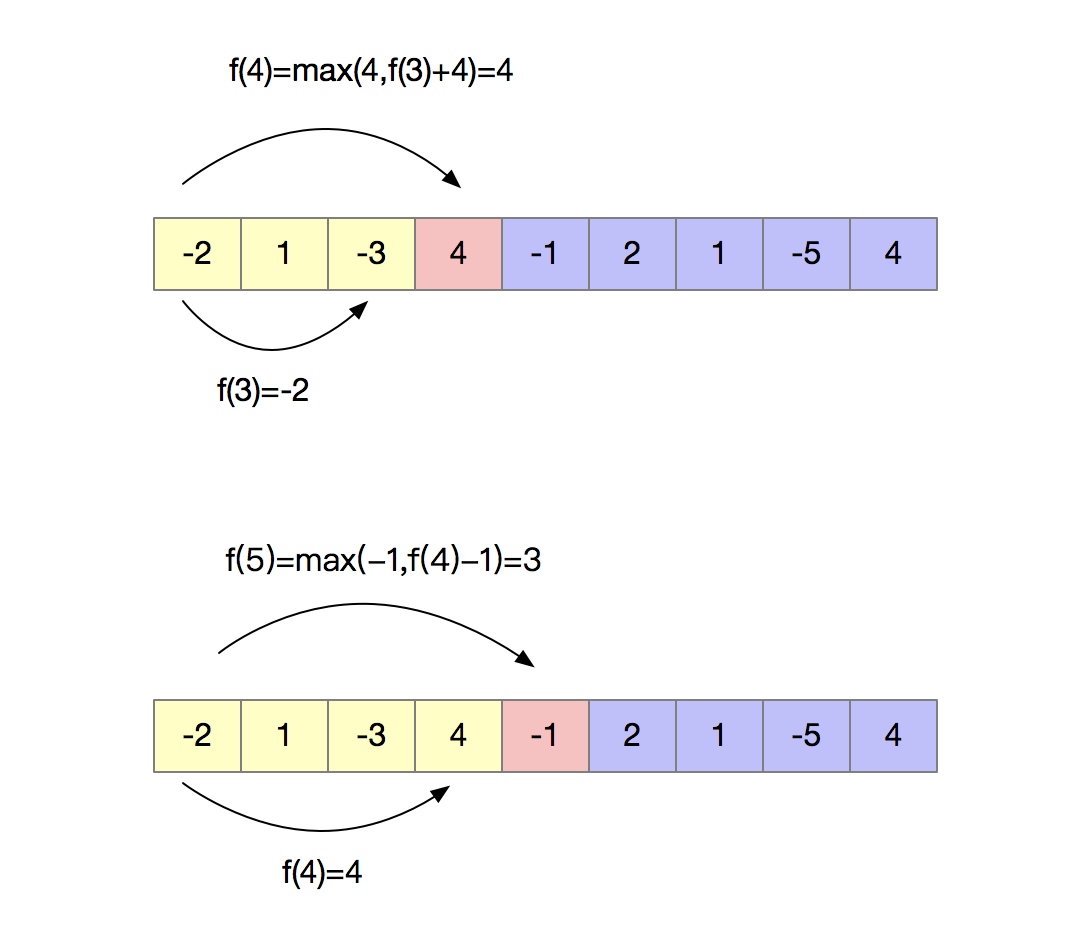
因為題目是求所有子陣列的和的最大值,我們可以假設以第i個數結尾的連續子陣列和的最大的值為f(i)。現在我們只需要求出所有的f(i),拿出其中最大的就是題目的解。
我們下面來看一下如何求解f(i)。對於以第i個數結尾的子陣列來說,f(i)要麼等於nums[i],要麼等於f(i-1)+nums[i],這取決於nums[i]和f(i-1)+nums[i]的大小。即f(i)=max(nums[i],f(i-1)+nums[i])。
class Solution:
def FindGreatestSumOfSubArray(self, array):
if array is None or len(array)==0:
return 0
n=len(array)
dp=[0]*n
dp[0]=array[0]
for i in range(1,n):
dp[i]=max(array[i],dp[i-1]+array[i])
return max(dp)
我們可以看到這裡的時間複雜度和空間複雜度都是O(n)。由於我們在求解f(i)的時候,只和f(i-1)和nums[i]有關,而和f(i-2)、f(i-3)...無關,所以,我們只需要一個變數去儲存f(i-1)就好了,這樣可以把空間複雜度減低為O(1)。下面我們來看一下程式碼如何實現。
def maxSubArray(array):
if array is None or len(array)==0:
return 0
n=len(array)
pre=array[0]
result=array[0]
for i in range(1,n):
pre=max(array[i],pre+array[i])
result=max(result,pre)
return result
