題目描述
輸入一個整數,輸出該數二進位制表示中1的個數。其中負數用補碼錶示。
補碼
解題前,我們先來了解一下補碼。在計算機系統中,數值都是用補碼來表示和儲存的。
而原碼就是數值的二進位制數表示,最高位1表示負數。
以32位數值舉例
1的原碼就是
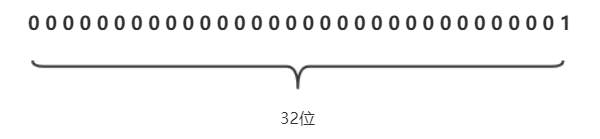
-1的原碼就是
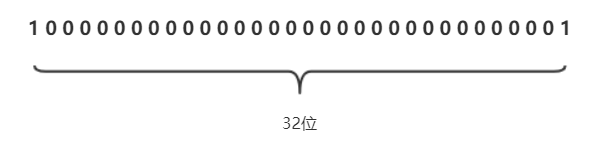
正數的補碼等於原碼
負數的補碼等於其原碼按位取反後(除了最高位)加1,比如-1的補碼就是32個1
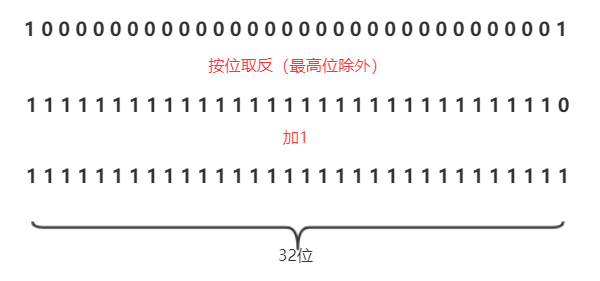
使用補碼的好處在於,可以將符號位和數值位統一處理,加法與減法也可以統一處理。
比如3 - 1,等價於3 + (-1),則對於計算機來說將3和-1的補碼直接相加就可以,計算過程如下圖所示。如果直接使用數值的原碼錶示,則不會得到正確的結果,感興趣的同學可以計算試一下,這裡不再贅述。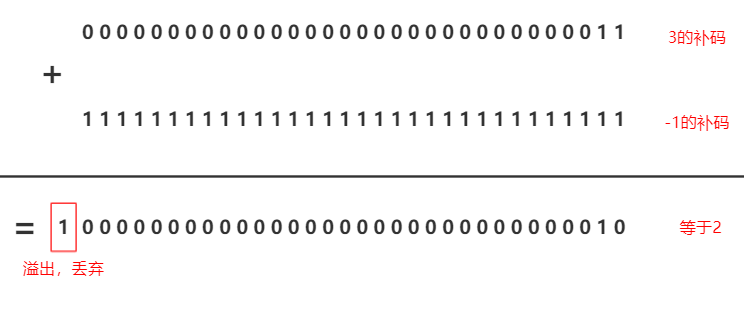
解法1
對於本題,首先想到的是將二進位制數一直右移,這樣的話該數的每一位都會依次成為最低位,然後將該數和1相與,計算1的個數。(由於1只有最低位是1,其他位都是0,某個數和它相與後,結果如果是1,就說明該數最低位是1,否則就是0)
按照以上思想,實現的程式碼如下,但是請注意,這樣的寫法是錯誤。沒有考慮負數的情況,和正數右移最高位補0不同的是,負數右移最高位補1,這樣就會有無數個1,導致死迴圈。
public int NumberOf1(int n)
{
int count = 0;
// 沒有考慮負數,一直不會等於0
while(n != 0)
{
if ((n & 1) == 1)
count++;
// 負數右移最高位補1
n >>= 1;
}
return count;
}既然將目標數右移和1與行不通,那麼我們可以反過來,將1不斷左移(從最低位到最高位每一位依次是1,其他位是0),然後和目標數相與來求1的個數。具體過程如下圖所示

實現程式碼
public int NumberOf1(int n)
{
int unit = 1, count = 0;
while (unit != 0)
{
if ((unit & n) != 0)
count++;
unit <<= 1;
}
return count;
}解法2
上面解法1的時間複雜度是O(n的位數),n有所少位就要迴圈多少次。可以利用一個小技巧,降低演算法的時間複雜度。
先來看一個例子,對於任意一個數將其減1,比如7
7的補碼錶示是

(7的補碼)
減1後為6,補碼錶示如下。如果再和7相與,得到的值仍為6。得到的值相當於把7從右邊數的第一個1被變成了0

(6的補碼)
比如6,再減1,為5,補碼錶示如下

(5的補碼)
如果再和6相與,得到的值為4。補碼錶示如下,得到的值相當於把6從右邊數的第一個1被變成了0

如果用負數進行測試,也是一樣的結果。
由此我們可以發現對於數值n,將n - 1後再和n相與,得到的值相當於將n從右邊數的第一個1變成0。n的二進位制表示中有多少個1,就能變多少次。實現程式碼如下,時間複雜度優化為O(n中1的個數)
實現程式碼
public int NumberOf1(int n)
{
int count = 0;
while (n != 0)
{
count++;
n = (n - 1) & n;
}
return count;
}