Unique Binary Search Trees leetcode java

愛做飯的小瑩子發表於2014-08-01
LeetCodeJava

題目：

Given n, how many structurally unique BST's (binary search trees) that store values 1...n?

For example,
Given n = 3, there are a total of 5 unique BST's. 

   1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3



題解：

 這道題我自己是沒啥思路的，感覺就是一種排列組合的計算，但是又不太會。。然後網上查了一下，說要用卡特蘭數。。

我下面的帶引號的講解引用Code Ganker(http://blog.csdn.net/linhuanmars/article/details/24761459)的了：

“這道題要求可行的二叉查詢樹的數量，其實二叉查詢樹可以任意取根，只要滿足中序遍歷有序的要求就可以。從處理子問題的角度來看，選取一個結點為根，就把結點
切成左右子樹，以這個結點為根的可行二叉樹數量就是左右子樹可行二叉樹數量的乘積，所以總的數量是將以所有結點為根的可行結果累加起來。寫成表示式如下：
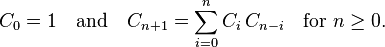
熟悉卡特蘭數的朋友可能已經發現了，這正是卡特蘭數的一種定義方式，是一個典型的動態規劃的定義方式（根據其實條件和遞推式求解結果）。所以思路也很明確了，維護量res[i]表示含有i個結點的二叉查詢樹的數量。根據上述遞推式依次求出1到n的的結果即可。

時間上每次求解i個結點的二叉查詢樹數量的需要一個i步的迴圈，總體要求n次，所以總時間複雜度是O(1+2+...+n)=O(n^2)。空間上需要一個陣列來維護，並且需要前i個的所有資訊，所以是O(n)。"

 

 

看到了一個解釋的更清楚的分析，轉自http://fisherlei.blogspot.com/2013/03/leetcode-unique-binary-search-trees.html：

“

   這題想了好久才想清楚。其實如果把上例的順序改一下，就可以看出規律了。 

      1         3     3      2      1
       \       /     /      / \      \
        3     2     1      1   3      2
       /     /       \                 \
      2     1         2                 3

 

   比如，以1為根的樹有幾個，完全取決於有二個元素的子樹有幾種。同理，2為根的子樹取決於一個元素的子樹有幾個。以3為根的情況，則與1相同。

    定義Count[i] 為以[0,i]能產生的Unique Binary Tree的數目，

    如果陣列為空，毫無疑問，只有一種BST，即空樹，
    Count[0] =1

    如果陣列僅有一個元素{1}，只有一種BST，單個節點
    Count[1] = 1

    如果陣列有兩個元素{1,2}， 那麼有如下兩種可能
    1                       2
     \                    /
       2                1
    Count[2] = Count[0] * Count[1]   (1為根的情況)
                  + Count[1] * Count[0]  (2為根的情況。

    再看一遍三個元素的陣列，可以發現BST的取值方式如下：
    Count[3] = Count[0]*Count[2]  (1為根的情況)
                  + Count[1]*Count[1]  (2為根的情況)
                  + Count[2]*Count[0]  (3為根的情況)

    所以，由此觀察，可以得出Count的遞推公式為
    Count[i] = ∑ Count[0...k] * [ k+1....i]     0<=k<i-1
    問題至此劃歸為一維動態規劃。

   [Note]
    這是很有意思的一個題。剛拿到這題的時候，完全不知道從那下手，因為對於BST是否Unique，很難判斷。最後引入了一個條件以後，立即就清晰了，即
    當陣列為 1，2，3，4，.. i，.. n時，基於以下原則的BST建樹具有唯一性：
   以i為根節點的樹，其左子樹由[1, i-1]構成， 其右子樹由[i+1, n]構成。

”

同時為了根據遞推式來寫程式，需要將遞推式簡化一下。

根據卡特蘭數，C0Cn+1，因為leetcode輸入的引數是n，所以為了避免混淆，這裡遞推式寫成Ct+1,初始值為C0 = 1。

原始的遞推式是： Ct+1 += Ci*Ct-i (0<= i <=t)

現在令變數num=t+1，那麼t=num-1

所以原始遞推式做變數替換得：Cnum += Ci*Cnum-1-i (0<= i <=num-1)

而num的取值範圍是[1, n]因為C0已知。

程式碼如下：

 1     public int numTrees(int n) {
 2         if(n == 0||n == 1)
 3             return 1;
 4         
 5         int[] C = new int[n+1];
 6         C[0] = 1;
 7      //遞推式是Ct+1 += Ci*Ct-i(0<= i <= t)
 8      //令num = t+1
 9      //則 t = num-1;
10      //因此遞推式化為：
11      //Cnum += Ci*Cnum-1-i(0<=i<=num-1, 1<=num<=n)
12      //C0 = 1
13 
14     for(int num=1;num<=n;num++){  
15         for(int i=0;i<=num-1;i++){  
16             C[num] += C[i]*C[(num-1)-i];  
17         }  
18     }
19         return C[n];
20     }

 

 

相關文章