動態規劃專題之---- Unique Binary Search Trees

標籤（空格分隔）： LeetCode

---

題目連結
參考博文

表示根本不知道什麼是卡特蘭數，百度的截圖

根據動態規劃解題步驟慢慢分析

1.分解子問題

根據題意分析，二叉搜尋樹不同原因在於。一個數列中的所有元素都可以成為祖先。
於是第一個子問題是每個數都可以作為祖先。我們可以遍歷數列。

然後確定一個數為祖先後，剩下n-1個數先分為兩撥，而這兩撥如何分？左子樹節點數從0開始一直到某個臨界值時，這樣過一遍就是完美了。

於是左子樹的子樹又可以根據這樣的遞推關係繼續往下面分。

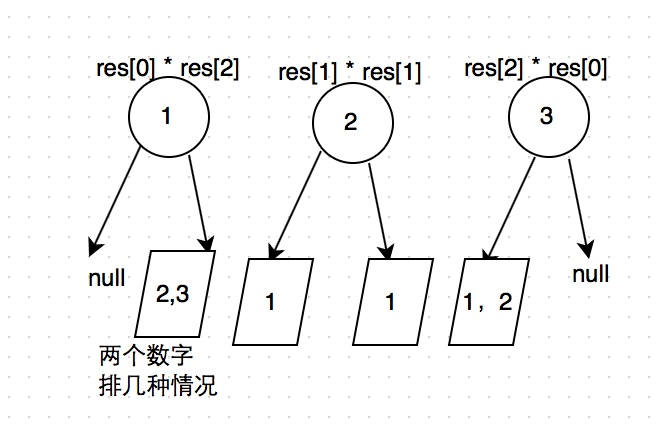
當祖先（根為數值為i時），左子樹最大的數為i-1。於是左子樹的元素個數可以從0增加到i-1。而右子樹的節點個數也可以依次增多。

這裡的n=3，不是說的根節點數字為3，而是說的當節點數為3的時候

2.確定狀態

dp[i]=j 表示當有i的節點時，BST的種類數目。

3.確定初始狀態

dp[0]=1; 沒有節點只有一種情況，空樹
dp[1]=dp[0]*dp[0]=1; 只有一個節點也是隻有一種情況

4.確定狀態轉移方程

int i;
 for(int j=0;j<i;j++){
    dp[i]+=dp[j]*dp[i-j-1];
 }

模擬一下輸入3的情況

i
i=1	dp[1]=dp[0]∗dp[0] dp[1]=dp[0]*dp[0]
i=2	dp[2]=dp[1]∗dp[0] dp[ 2]=dp[ 1]*dp[0]	dp[2]=dp[0]∗dp[1] dp[ 2]=dp[0]*dp[ 1]
i=3	dp[3]=dp[2]∗dp[0] dp[ 3]=dp[ 2]*dp[0]	dp[3]=dp[1]∗dp[1] dp[ 3]=dp[1]*dp[1]	dp[3]=dp[0]∗dp[2] dp[3]=dp[0]*dp[2]

1. i=1 表示只有一個節點的情況
2. i=2 表示兩個節點的情況，這個時候就可以利用case1中計算出來的結果dp[1]了。
3. i=3 表示三個節點的情況，這個時候就可以利用case2中計算出來的結果了。

對應i=3的時候

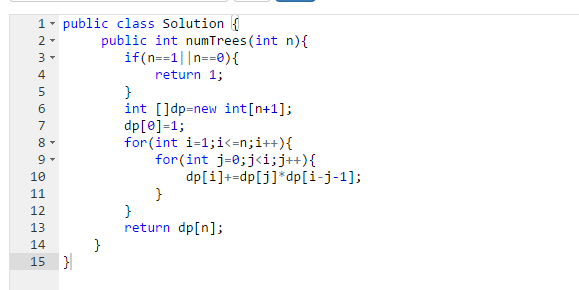
public class Solution{
    public int numTrees(int n){
        if(n==0||n==1){
            return 1;
        }
        int []dp=new int[n+1];
        //每個數都可以做根節點，相當於有這麼多個節點時
        for(int i=1;i<=n;i++){

            //i為根節點時，左子樹從0開始增加
            for(int j=0;j<i;j++){
                dp[i]+=dp[j]*dp[i-j-1];
            }
        }
        return dp[n];
    }

}