題目:
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
How many possible unique paths are there?
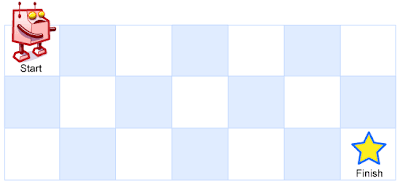
Above is a 3 x 7 grid. How many possible unique paths are there?
Note: m and n will be at most 100.
題解:
其實跟爬梯子挺類似的,按個就是隻能往上爬,這個就是方向可以換了下。同樣想法動態規劃。
分析方法也一樣的,想想要到最右下角。到達右下角的方法只有兩個,從上面往下,和從右面往左。
利用到達終點的唯一性,就可以寫出遞推公式(dp[i][j]表示到座標(i,j)的走法數量):
dp[i][j] = dp[i-1][j] + dp[i][j-1]
初始條件的話,當整個格子只有一行,那麼到每個格子走法只有1種;只有一列的情況同理。
所以,理解的這些,程式碼就非常好寫了。
通常來講,我們會初始dp陣列為dp[m+1][n+1]。但是這裡的話,因為dp[i][j]是表示座標點,所以這裡宣告dp[m][n]更容易理解。
程式碼如下:
1 public static int uniquePaths(int m, int n){
2 if(m==0 || n==0) return 0;
3 if(m ==1 || n==1) return 1;
4
5 int[][] dp = new int[m][n];
6
7 //只有一行時,到終點每個格子只有一種走法
8 for (int i=0; i<n; i++)
9 dp[0][i] = 1;
10
11 // 只有一列時,到終點每個格子只有一種走法
12 for (int i=0; i<m; i++)
13 dp[i][0] = 1;
14
15 // for each body node, number of path = paths from top + paths from left
16 for (int i=1; i<m; i++){
17 for (int j=1; j<n; j++){
18 dp[i][j] = dp[i-1][j] + dp[i][j-1];
19 }
20 }
21 return dp[m-1][n-1];
22 }
2 if(m==0 || n==0) return 0;
3 if(m ==1 || n==1) return 1;
4
5 int[][] dp = new int[m][n];
6
7 //只有一行時,到終點每個格子只有一種走法
8 for (int i=0; i<n; i++)
9 dp[0][i] = 1;
10
11 // 只有一列時,到終點每個格子只有一種走法
12 for (int i=0; i<m; i++)
13 dp[i][0] = 1;
14
15 // for each body node, number of path = paths from top + paths from left
16 for (int i=1; i<m; i++){
17 for (int j=1; j<n; j++){
18 dp[i][j] = dp[i-1][j] + dp[i][j-1];
19 }
20 }
21 return dp[m-1][n-1];
22 }