Kruskal 重構樹
定義
在跑 Kruskal 的過程中我們會從小到大加入若干條邊。現在我們仍然按照這個順序。
首先新建 \(n\) 個集合,每個集合恰有一個節點,點權為 \(0\)。
每一次加邊會合並兩個集合,我們可以新建一個點,點權為加入邊的邊權,同時將兩個集合的根節點分別設為新建點的左兒子和右兒子。然後我們將兩個集合和新建點合併成一個集合。將新建點設為根。
不難發現,在進行 \(n-1\) 輪之後我們得到了一棵恰有 \(n\) 個葉子的二叉樹,同時每個非葉子節點恰好有兩個兒子。這棵樹就叫 Kruskal 重構樹。
舉個例子:
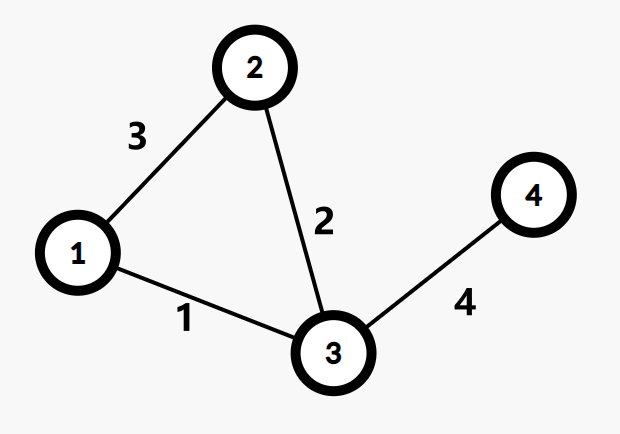
這張圖的 Kruskal 重構樹如下:
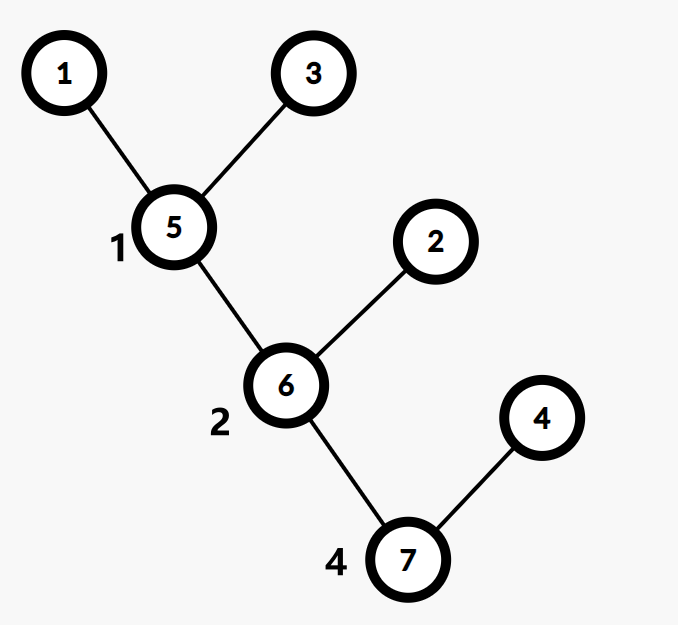
性質
不難發現,原圖中兩個點之間的所有簡單路徑上最大邊權的最小值 = 最小生成樹上兩個點之間的簡單路徑上的最大值 = Kruskal 重構樹上兩點之間的 LCA 的權值。
也就是說,到點 \(x\) 的簡單路徑上最大邊權的最小值 \(\leq val\) 的所有點 \(y\) 均在 Kruskal 重構樹上的某一棵子樹內,且恰好為該子樹的所有葉子節點。
我們在 Kruskal 重構樹上找到 \(x\) 到根的路徑上權值 \(\leq val\) 的最淺的節點。顯然這就是所有滿足條件的節點所在的子樹的根節點。
如果需要求原圖中兩個點之間的所有簡單路徑上最小邊權的最大值,則在跑 Kruskal 的過程中按邊權大到小的順序加邊。