常見時間複雜度
二分查詢:\(O(\log_2N)\)
陣列
陣列的行序儲存和列序儲存
a[row][col]
行序:a[i][j] = &a[0][0] + (i * col + j) * size
a[0][0] a[0][1] ... a[0][col - 1]
a[1][0] a[1][1] ... a[1][col - 1]
先增加 \(j\),當一行填滿(\(j=\text{col}-1\)),再增加 \(i\) 。

列序:a[i][j] = &a[0][0] + (j * row + i) * size
a[0][0] a[1][0] ... a[row - 1][0]
a[0][1] a[1][1] ... a[row - 1][1]
先增加 \(i\),當一列填滿(\(i=\text{row}-1\)),再增加 \(j\) 。

陣列的儲存順序 | C 語言中文網
行號和列號的位置是不變的(永遠是
a[行][列])以列序為主
String
KMP 演算法
void getNext(string str, int next[]) { // next[j] 表示字元 str[j] 前面的子串的相等前字尾的長度
auto len = str.length();
next[0] = -1;
int k = -1;
int j = 0;
while (j < len - 1) { // 在賦值時是將包含 str[j] 在內的子串的前字尾的長度賦給 next[j + 1],因此 j 只用迴圈到 len - 2。
// str[k] 表示字首之後,str[j] 表示字尾之後。
if (k == -1 || str[j] == str[k]) { // 字首之後和字尾之後相等,說明相等前字尾可以延長 1 位。
++j;
++k;
// 最佳化 KMP 演算法加入的判斷
if (str[j] != str[k]) {
next[j] = k;
} else { // 在匹配時,如果字尾之後失配,那麼就讓字首之後再次與之嘗試匹配。因此如果字首之後和字尾之後相等,就一定再次失配。因此這裡直接遞迴 k 的值並將其賦給 next[j]。
next[j] = next[k];
}
} else {
k = next[k]; // 遞迴到更短的字首中去判斷
}
}
}
部落格園:從頭到尾徹底理解 KMP
矩陣的壓縮儲存
對稱陣
對於如下矩陣:

以深灰色為對稱軸,由於矩陣內資料對稱,因此只需要將任意一邊的資料儲存起來即可。
需要儲存的元素為:

各個元素對應在一維陣列中的位置示意圖:

矩陣座標轉換陣列座標
陣列下標 k 等於矩陣元素 \(a_{ij}\) 上面的 \(i - 1\) 行的元素個數加上當前行前面的元素個數(注意矩陣從 \(a_{11}\) 開始計數)
前 i -1 行的元素個數
等差數列求和,\(a_1=1,a_n=i-1,n=i-1\) (每行的元素個數就是它的行序)
\(S_n = \dfrac{(a_1+a_n)n}{2}=\dfrac{i(i-1)}{2}\)
當前行前面的元素個數
\(j-1\)
因此,可以得到 \(k=\dfrac{i(i-1)}{2}+j-1\)
上面的公式儲存的是下三角的元素。對於上三角的元素,由於 \(a_{ij}=a_{ji}\),因此上三角的元素位置公式可以將上式中的 \(i\) 與 \(j\) 互換得到。即 \(k_{上三角}=\dfrac{j(j-1)}{2}+i-1\)
稀疏矩陣
只儲存非零元,非零元的個數以及矩陣的大小。非零元透過 (行標, 列標, 值) 的三元組表示。
三元組順序表
class Triple {
int i, j, val;
};
class TSMatrix {
Triple data[number]; // 三元組陣列
int n, m; // 矩陣的行數和列數
int num; // 非零元個數
};
行邏輯連結的順序表
三元組順序表每次提取指定元素都要遍歷整個三元組陣列,效率很低。因此提出了三元組順序表的升級版——行邏輯連結的順序表。
行邏輯連結的順序表在三元組順序表的基礎上加入了一個用於記錄矩陣中每行的首非零元在三元組陣列中的位置的陣列。
class RLSMatrix {
Triple data[MAXSIZE + 1];
int rpos[MAXRC + 1];
int n, m;
int num;
};

對於上面的矩陣,採用行邏輯連結的順序表儲存時,需要做兩個工作:
- 將矩陣中的非零元儲存到三元組陣列。

- 使用陣列 rpos 記錄矩陣中每行的首非零元在 data 中的位置。

這樣,當我們提取元素時,就可利用 rpos 陣列定位要訪問的位置區間來提高效率。
void display(RLSMatrix M) {
for (int i = 1; i <= M.m; ++i) {
for (int j = 1; j <= M.n; ++j) {
int flag = 0; // 標記是否在 data 陣列中找到該位置的元素
if (i + 1 <= M.m) // 如果不是最後一行(最後一行的話 k = rpos[i + 1] 會越界)
{
for (int k = M.rpos[i]; k < M.rpos[i + 1]; ++k) // 透過 rpos 陣列定位這一行在 data 陣列中的位置
{
if (i == M.data[k].i && j == M.data[k].j) // 找到對應元素
{
printf("%d ", M.data[k].val);
flag = 1;
break;
}
}
if (flag == 0) // 沒有找到對應元素
{
printf("0 ");
}
} else // 最後一行
{
for (int k = M.rpos[i]; k <= M.num; ++k) // 定位
{
if (i == M.data[k].i && j == M.data[k].j) // 找到對應元素
{
printf("%d ", M.data[k].val);
flag = 1;
break;
}
}
if (flag == 0) {
printf("0 ");
}
}
}
printf("\n"); // 每行輸出完輸出一個換行
}
}
行邏輯連結的順序表
十字連結串列法
為解決陣列不便於插入或刪除的問題,提出了十字連結串列法。
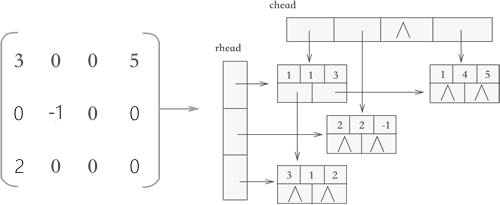
如圖,有一個行陣列和一個列陣列,陣列中存的是該行(列)所有非零元的連結串列。

class OLNode {
int i, j, val;
OLNode *right, *down;
}
十字連結串列法詳解
稀疏矩陣的轉置演算法
轉置:\(a_{ij}=a_{ji}\)
對於使用三元組順序表或行邏輯連結的順序表儲存的矩陣,在轉置時需要完成以下三步:
- 將矩陣的行數 \(m\) 和列數 \(n\) 互換。
- 將三元組表中每個元素的 \(i\) 和 \(j\) 互換。
- 重新排列三元組表中的元素順序。
簡單實現思路:不斷遍歷儲存矩陣的三元組表,每次都從中取出 \(j\) 最小的那一個元素(如果有多個,則按照他們原來在三元組中的次序依次取出),互換 \(i\) 和 \(j\),然後儲存到一個新的三元組表中
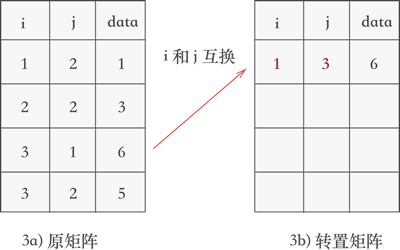
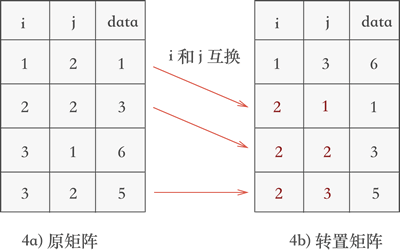
該演算法的時間複雜度為 \(O(n^2)\)
稀疏矩陣的轉置演算法
樹與二叉樹
- 度
- 一個結點含有的子結點的個數
- 樹中的度指的是結點擁有的子樹數量
樹的常用定理
- 所有結點的度數之和是邊數的 2 倍(這裡的度是指一般的度)
- 樹中的邊數等於結點數減 1(樹根沒有向上走的邊)
- 正則二叉樹的葉子數比度為 2 的結點數多一個 (\(n_0=n_2+1\))
正則二叉樹:每個分支點的出度都為 2
二叉樹
二叉樹的遍歷
// 遞迴中序遍歷
void InOrderTraverse(Node *node) {
if (node) {
InOrderTraverse(node->lchild); // 遍歷左孩子
displayElem(node); // 訪問結點
InOrderTraverse(node->rchild); // 遍歷右孩子
}
}
二叉樹先序遍歷
確定了二叉樹的遍歷方式,就相當於確定了一個將二叉樹轉換為線性表的規則。
透過前序和中序序列還原二叉樹
任何二叉樹都可由中序序列和另一個序列唯一確定
- 確定根結點(前序的第一個結點,後序的最後一個結點,層序的第一個節點),根據根結點將中序分割成左子樹和右子樹。畫出根結點和左右分支。
- 將左子樹和右子樹看成新的樹,重複第一步。
寫之前把前序和中序抄下來,先序每分析一個結點,就劃掉一個,並在中序中把這個結點變成牆(很粗的分割線)。當其左右孩子確認下來後,將其塗黑。
例:前序:ABCDEF,中序:CBAEDF
A 是根結點,將中序分為:CB[A]EDF,CB 是左子樹,EDF 是右子樹。畫出根結點和左右兩個分支。
接下來根結點是 B,將中序分為 C[B][A]EDF,C 是左子樹,沒有右子樹。
接下來 C。
接下來根結點是 D,將中序分為 [C][B][A]E[D]F,E 是左子樹,F 是右子樹。
using size_type = string::size_type;
// 返回由 [LVR_begin, LVR_end) 構建的二叉樹的根結點;VLR 是先序,LVR 是中序
Node *createBiTreeByVLRAndLVR(const string &VLR, const string &LVR, size_type LVR_begin, size_type LVR_end) {
static size_type i;
Node *root{};
if (LVR_begin < LVR_end) {
root = new Node(VLR[i++]); // 先序的首結點為根結點
auto LVR_root = LVR.find(root->index); // 在中序中定位根結點
root->lchild = createBiTreeByVLRAndLVR(VLR, LVR, LVR_begin, LVR_root);
root->rchild = createBiTreeByVLRAndLVR(VLR, LVR, LVR_root + 1, LVR_end);
}
return root;
}
透過層序和中序序列還原二叉樹
using iter = vector<int>::iterator;
// 返回由 [LVR_begin, LVR_end) 構建的二叉樹的根結點;LT 是層序,LVR 是中序
Node *createBiTreeByLTAndLVR(const vector<int> <, iter LVR_begin, iter LVR_end) {
Node *root{};
if (LVR_begin < LVR_end) {
iter LVR_root;
for (int i: LT) {
if ((LVR_root = find(LVR_begin, LVR_end, i)) != LVR_end) { // 遍歷層序,第一個屬於該子樹的結點就是該子樹的根結點
break;
}
}
root = new Node(*LVR_root);
root->lchild = createBiTreeByLTAndLVR(LT, LVR_begin, LVR_root);
root->rchild = createBiTreeByLTAndLVR(LT, LVR_root + 1, LVR_end);
}
return root;
}
線索二叉樹
藉助線索可以在不使用遞迴或棧的條件下遍歷線索二叉樹。後繼線索可以為我們指明當前子樹遍歷完成後應該進入哪個子樹。
typedef enum {Link, Thread} PointerTag; // 指示指標域儲存的是孩子還是前驅後繼的列舉
class Node {
int val; // 資料域
Node *lchild, *rchild; // 左、右孩子指標域
PointerTag Ltag, Rtag; // 標誌域
};
對二叉樹進行線索化
// 中序對二叉樹進行線索化
void InOrderThreading(Node *node) {
static Node *pre = nullptr; // 上一次訪問的結點,即前驅
if (node) { // 如果當前結點存在
InOrderThreading(node->lchild); // 遞迴左子樹進行線索化
// 如果當前結點沒有左孩子,寫入前驅
if (!node->lchild) {
node->Ltag = Thread;
node->lchild = pre;
}
// 如果前驅沒有右孩子,寫入後繼
if (pre && !pre->rchild) {
pre->Rtag = Thread;
pre->rchild = node;
}
pre = node; // 更新前驅
InOrderThreading(node->rchild); // 遞迴右子樹進行線索化
}
}
在兩條遞迴語句中間的語句相當於遍歷二叉樹中的訪問操作。如果把它放到兩條遞迴語句前面,就變成前序線索二叉樹。
遍歷線索二叉樹
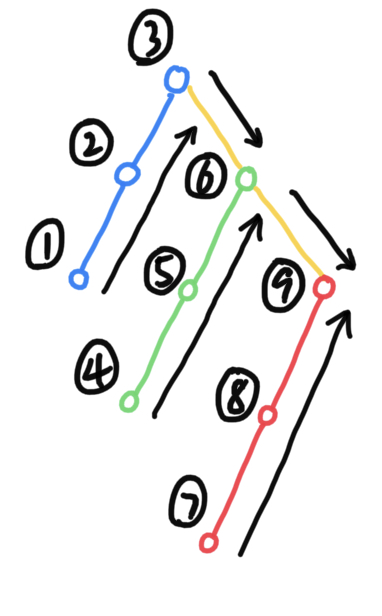
// 中序遍歷線索二叉樹
void InOrderThraverse(Node *node) {
while (node) {
while (node->Ltag == Link) { // 移步到最左下的結點
node = node->lchild;
}
cout << *node << " "; // 訪問結點
// 如果結點儲存了後繼,就直接訪問後繼
while (node->Rtag == Thread && node->rchild != NULL) {
node = node->rchild;
cout << *node << " ";
}
// 如果 rchild 儲存的不是後繼,那麼 rchild 就是右子樹。進入右子樹開始新一輪中序遍歷。
node = node->rchild;
}
}
線索二叉樹
雙向線索二叉樹
線索化
線上索二叉樹的基礎上,新增一個頭結點,其左孩子指向二叉樹的樹根,右孩子指向最後一個結點。這樣就可以反向遍歷(中序)二叉樹:
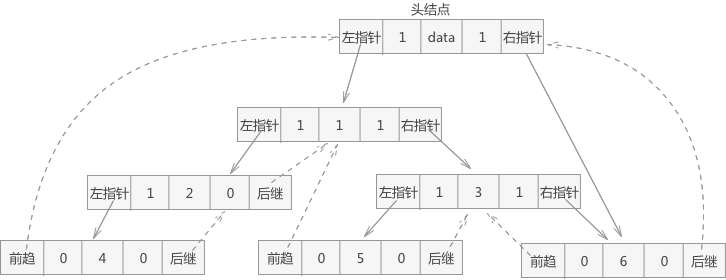
// 建立雙向線索連結串列
void DoubleThreading(Node *&head, Node *tree) {
// 初始化頭結點
head = new Node;
head->Ltag = Link;
head->Rtag = Link;
// 如果樹本身是空樹
if (!tree) {
head->lchild = head;
head->rchild = head;
} else {
auto pre = head; // 前驅
head->lchild = tree; // 頭結點的左孩子指向樹根
pre = InOrderThreading(tree, pre); // 稍作修改的 InOrderThreading 函式,從外部接收 pre 引數,並返回最後的 pre 引數,即尾結點。
pre->rchild = head;
pre->Rtag = Thread;
head->rchild = pre;
}
}
正向遍歷
和普通線索二叉樹的區別是,while 迴圈判斷的條件不是 while (node),而是 while (node != head) 以及 while (node->rchild != head)
// 中序正向遍歷雙向線索二叉樹
void InOrderThraverse(Node *head) {
Node *node = head->lchild;
while (node != head) {
while (node->Ltag == Link) {
node = node->lchild;
}
cout << *node << " ";
while (node->Rtag == Thread && node->rchild != head) {
node = node->rchild;
cout << *node << " ";
}
node = node->rchild;
}
}
逆向遍歷
逆向遍歷只要把右孩子當作左孩子,左孩子當作右孩子,然後正常遍歷即可。
這時相當於右子樹和自己是同一分支,左子樹是另一分支。
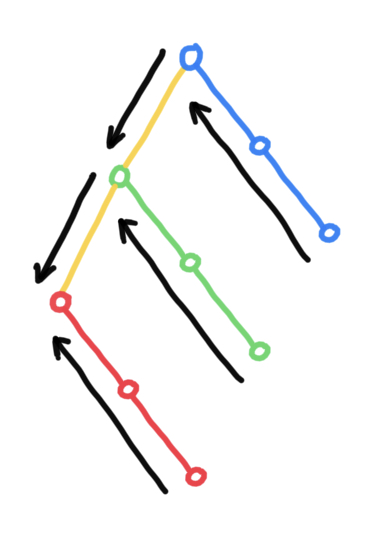
// 中序逆向遍歷線索二叉樹
void InOrderThraverse(Node *head) {
Node *node = head->rchild;
while (node != head) {
while (node->Rtag == Link) { // 移步到最右下的結點
node = node->rchild;
}
cout << *node << " "; // 訪問結點
// 如果結點儲存了前驅,就直接訪問前驅
while (node->Ltag == Thread && node->lchild != head) {
node = node->lchild;
cout << *node << " ";
}
// 如果 lchild 儲存的不是前驅,那麼 lchild 就是左子樹。進入左子樹開始新一輪中序遍歷。
node = node->lchild;
}
}
雙向線索二叉樹
樹
樹與二叉樹的區別:
- 二叉樹是有序樹。
- 樹的度指樹中最大的度。因此度為 2 的樹不能是空樹。而二叉樹可以是空樹。
樹的孩子兄弟表示法
其實和二叉樹的儲存結構是一樣的,這樣就將樹轉化為了二叉樹。樹轉化為二叉樹後,原來的兄弟節點變成了右子樹。於是樹就變成了一個由左分支串起來的一堆兄弟節點子樹。
樹轉化為二叉樹時,父結點的第一個孩子不變,同一父結點的其餘所有孩子連到第一個孩子上。
二叉樹還原成樹時,左孩子不變,右孩子連到自己的父結點上。
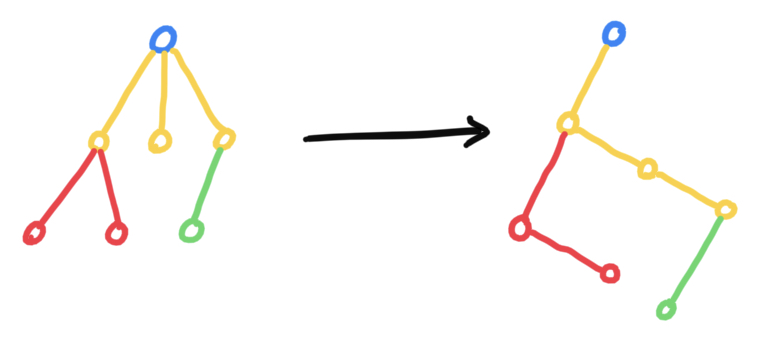

class TreeNode {
int val;
TreeNode *nextSon, *nextBro;
}
樹的遍歷
先根遍歷:先訪問根結點,再按照從左到右的順序依次訪問每一棵子樹。先根遍歷對應二叉樹的先序遍歷。
後根遍歷:先從左到右依次訪問每一棵子樹,再訪問根結點。後根遍歷對應二叉樹的中序遍歷。
森林
森林轉化為二叉樹
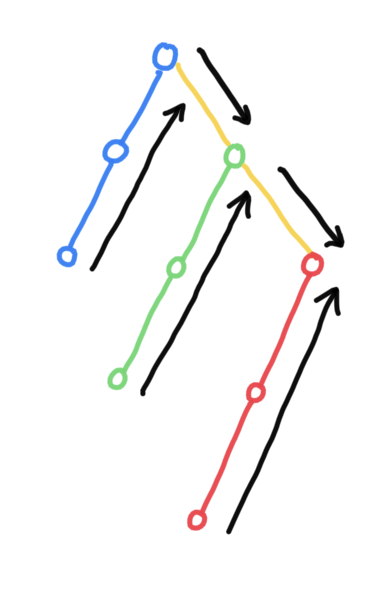
前面說過,中序訪問的二叉樹可以分成左右兩個部分,左子樹和自己是同一分支,右子樹是另一分支(相當於右分支串了一堆左子樹)。因此,可以把第一棵樹作為第一個左子樹,第二棵樹作為第二個左子樹,...
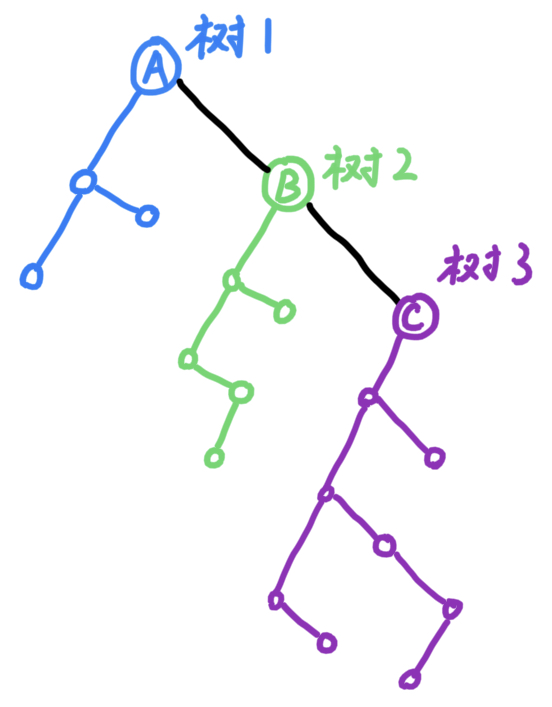
具體操作:
- 將森林中所有樹轉化為二叉樹
- 將第一課樹的樹根作為整個森林的樹根,其他樹的樹根看作第一棵樹根結點的兄弟節點,採用孩子兄弟法將所有樹進行連線。
森林轉化為二叉樹後,其前序遍歷和中序遍歷訪問結點的順序是不變的。
森林的遍歷
先序遍歷
相當於二叉樹的先序遍歷
- 訪問森林中第一棵樹的根結點
- 先根遍歷根結點的子樹
- 去掉第一棵樹,重複
中序遍歷
相當於二叉樹的中序遍歷
- 中序遍歷第一棵樹的根結點的子樹
- 訪問第一棵樹的根結點
- 去掉第一棵樹,重複
樹與等價問題
- \(x\) 關於 \(R\) 的等價類
- \([x]_R=\{y\mid y\in S\land xRy\}\)
- \(x\) 稱為等價類 \([x]\) 的表示元素
- \(R\) 的不同等價類的個數叫做 \(R\) 的秩
e.g.
\(R\) 是自然數集合 \(\N\) 上的模 3 等價關係 \(\equiv_3\),試給出 \(\equiv_3\) 所確定的等價類。
\(\begin{aligned} [0]_3=\{0, 3, 6, \ldots\}\\ [1]_3=\{1, 4, 7, \ldots\}\\ [2]_3=\{2, 5, 8, \ldots\} \end{aligned}\)
劃分等價類
- 將每個元素看成單個集合。
- 如果有等價關係偶對 \((x,y)\),且兩個元素來自不同集合,則將兩個集合合併。
- 剩下的所有非空集合就是等價類。
用森林表示一個劃分 \(S=S_1\cup S_2\cup\cdots\cup S_n\)
一棵樹就是一個等價類。樹根是這個等價類的代表元素。
集合的合併:一個根指向另一個根
class Node {
int val;
Node *parent;
};
class MFSet {
int n;
Node nodes[MAXSIZE];
};
改進:
- 每次歸併讓深度少的指向深度多的
- Find 時壓縮路徑
並查集

知乎:演算法學習筆記(1) : 並查集
初始化
建立一個陣列或 map,用於儲存每個結點的父節點。初始時每個結點的父節點就是自己。
int parent[SIZE];
inline void init(int n) {
for (int i = 0; i < n; ++i) {
parent[i] = i;
}
}
查詢
int findParent(int i) {
return i == parent[i] ? i : (parent[i] = findParent(parent[i])); // 若自己不是集合的代表元素,那麼集合的代表元素就是父結點所屬集合的代表元素
}
合併
inline void merge(int v1, int v2) {
parent[findParent(v2)] = findParent(v1); // 把 v2 所屬集合歸併到 v1 所屬集合
}
哈夫曼樹(最優二叉樹)
- WPL
- 樹的所有葉子結點的帶權路徑長度之和,稱為樹的帶權路徑長度。
把二叉樹中所有非葉子結點的權加起來就是二叉樹的帶權路徑長度
構造方法
將所有葉子按權值升序排列。每次找到兩個權值最小的兩片葉子,將它們合併起來,不斷重複。
哈夫曼編碼
如果對每個字元設計長度不同的編碼,且讓電文中出現次數較多的字元采用較短的編碼,則可以減短電文的總長。利用字首編碼解決譯碼二義性的問題。
- 字首編碼
- 長度不等的編碼,任一個編碼都不是另一個編碼的字首。
利用二叉樹設計二進位制字首編碼
左分支表示 0 ,右分支表示 1 ,以字元的出現頻率作為權值構造最優二叉樹。
譯碼時根據編碼指引探索二叉樹( 0 往左走,1 往右走),找到對應的字元葉子。
實現
對於給定的葉子個數,其正則二叉樹的結點個數是已知的 (\(n=2n_0-1\)),因此可以用線性結構儲存哈夫曼二叉樹。
構造一個長度為 \(2n - 1\) 的陣列,前 \(n\) 個用於儲存葉子,後 \(n - 1\) 個用於儲存父結點。
typedef struct {
unsigned weight;
unsigned parent
unsigned lchild, rchild;
} HTNoode, *HuffmanTree;
typedef char **HuffmanCode; // 由於每個字元的編碼長度不同,因此應該用動態陣列儲存哈夫曼編碼。HuffmanCode 是指向儲存所有字元的哈夫曼編碼的二維陣列的指標。
分配哈夫曼編碼分為兩步:
- 構造哈夫曼樹
- 從葉子到根遍歷哈夫曼樹,確定每個字元的哈夫曼編碼
也可以從根到葉子遍歷二叉樹
確定哈夫曼編碼
void HuffmanCoding(HuffmanTree HT, HuffmanCode *HC, int n) { // HT 為哈夫曼樹(陣列),HC 為儲存所有哈夫曼編碼的字串陣列,n 為結點的個數。
*HC = (HuffmanCode)malloc((n + 1) * sizeof(char*)); // HC[0] 不用,因此申請 n + 1 個空間。
char *temp = (char*)malloc(n * sizeof(char)); // 臨時存放結點哈夫曼編碼的字串
temp[n - 1] = '\0'; // 每次從臨時字串倒數第二個位置開始反向填寫哈夫曼編碼
for (int i = 1; i <= n; ++i) {
// 從葉子結點出發,得到的哈夫曼編碼是逆序的,需要在字串陣列中逆序存放
int flag = n - 1; // 上一個編碼填在臨時陣列的哪裡
int cur = i; // 當前結點在陣列中的位置
int parent = HT[i].parent; // 父結點在陣列中的位置
// 一直尋找到根結點
while (parent != 0) {
// 如果該結點是左孩子則編碼為 0 ,否則編碼為 1 。
if (HT[parent].left == cur)
temp[--flag] = '0';
else
temp[--flag] = '1';
// 更新父子結點
cur = parent;
parent = HT[parent].parent;
}
// 分配哈夫曼編碼
(*HC)[i] = (char*)malloc((n - flag) * sizeof(char));
strcpy((*HC)[i], &temp[start]);
}
free(temp);
}
哈夫曼編碼
圖
- 圖
- 無向圖的邊數不超過 \(\dfrac{n(n-1)}{2}\)
- 有向圖的邊數不超過 \(n(n-1)\)
網就是邊帶權的圖
圖的鄰接矩陣表示
若存在邊 [i, j],則 a[i, j] 設為 1 ,否則設為 0 。
圖的鄰接矩陣對角元一般為 0 。
在網中,a[i, j] 的值是邊 [i, j] 的權。若邊不存在,則 a[i, j] 設為 \(\infty\) 。
網的鄰接矩陣對角元一般為 \(\infty\) 。
第 i 行的邊數表示 \(v_i\) 的出度,第 j 列的邊數表示 \(v_j\) 的入度。
圖的鄰接表儲存
結點用陣列儲存,每個結點都有一個儲存其所有邊的連結串列。

class Graph {
int n; // 圖的頂點數
list<pair<int, int>> *adj; // 鄰接表,儲存邊的終點和邊的權 (v, w) 。
public:
explicit Graph(int V);
void addEdge(int u, int v, int w);
};
Graph::Graph(int i) : n(i) {
adj = new list<pair<int, int>>[n];
}
void Graph::addEdge(int u, int v, int w) {
adj[u].emplace_back(v, w);
adj[v].emplace_back(u, w);
}
逆鄰接表:儲存入弧
十字連結串列
將有向圖的鄰接表和逆鄰接表結合在一起就得到了十字連結串列
class Node {
string name;
Arc *firstIn;
Arc *firstOut;
};
class Arc {
Node *from;
Node *to;
int info;
Arc *nextIn;
Arc *nextOut;
}
鄰接多重表
類似十字連結串列
class Node {
string name;
Arc *firstArc;
};
class Arc {
bool mark;
int info;
Node *iNode;
Node *jNode;
Arc *iArc;
Arc *jArc;
}
圖的遍歷
鄰接表儲存方式的時間複雜度:\(O(n+e)\)
鄰接矩陣儲存方式的時間複雜度:\(O(n^2)\)
兩種遍歷方法分別生成兩種生成樹。
DFS
對每一個可能的分支路徑深入到不能再深入為止
類似樹的先序遍歷
- 訪問頂點 v ;
- 依次從未被訪問的 v 的鄰接點出發,對圖進行 DFS;直至圖中所有和 v 有相通路徑的頂點都被訪問;
- 若此時圖中尚有頂點未被訪問,則從一個未被訪問的頂點出發,重新進行 DFS,直到圖中所有頂點均被訪問過為止。
構造深度優先樹的時候是沿著樹支往下延伸
可以使用 stack 實現:
// 假設此時已經遍歷所有結點,並找到了一個未訪問過的頂點 v 。
// 非遞迴實現
void DFS(int v) {
stack<int> nodeStk;
nodeStk.push(v);
cout << v + 1 << " ";
visited[v] = true;
while (!nodeStk.empty()) {
int top = nodeStk.top();
bool isAllVisited = true;
for (int i = 0; i < n; ++i) {
if (adjMatrix[top][i] && !visited[i]) {
nodeStk.push(i);
cout << i + 1 << " ";
visited[i] = true;
isAllVisited = false;
break;
}
}
if (isAllVisited) {
nodeStk.pop();
}
}
}
// 遞迴實現
void DFS(int v) {
cout << v + 1 << " ";
visited[v] = true;
for (int i = 0; i < n; ++i) {
if (adjMatrix[i][v] && !visited[i]) {
DFS(i);
}
}
}
BFS
類似樹的層次遍歷
- 從頂點 v 出發,訪問 v 。
- 訪問 v 的所有鄰接點。
- 分別訪問所有鄰接點的鄰接點。
- 重複 3 。
構造廣度優先樹的時候是一層一層構造
可以使用 queue 實現
// 假設此時已經遍歷所有結點,並找到了一個未訪問過的頂點 v 。
// 非遞迴實現
void BFS(int v) {
queue<int> nodeQue;
nodeQue.push(v);
visited[v] = true;
while (!nodeQue.empty()) {
int front = nodeQue.front();
nodeQue.pop();
cout << front + 1 << " ";
for (int i = 0; i < n; ++i) {
if (adjMatrix[front][i] && !visited[i]) {
nodeQue.push(i);
visited[i] = true;
}
}
}
}
圖的連通性
最小生成樹
- 最小生成樹(Minimum Cost Spanning Tree, MST)
- 樹上各邊的權值總和最小的生成樹
普里姆演算法(Prim 演算法)
適合稠密網
不斷選擇到集合距離最近的頂點
從一個平凡圖 \(U\) 開始,逐步增加 \(U\) 中的頂點,直至圖中的頂點數與原圖 \(V\) 相同,可稱為 "加點法" 。
在每次加點前,繪製一個頂點 \(v_i\) 到 \(U\) 的最短邊長度表。如果頂點 \(v_i\) 在 \(U\) 中,則 \(v_i\) 到 \(U\) 的最短邊長度為 \(0\) 。如果頂點 \(v_i\) 不鄰接 \(U\),則最短邊長度為 \(\infty\) 。
C 語言中文網:普里姆演算法
克魯斯卡爾演算法 (Kruskal 演算法)
適合稀疏網
將邊按權值升序排序,不斷選邊進來(不能形成環)。(選邊法)
- 對各頂點賦予不同的標記。
- 對所有邊按權值升序排序。
- 遍歷所有邊,若邊的兩頂點標記不同,則可以將該邊加入生成樹,同時將兩頂點的標記置為相同(原先和兩頂點標記相同的頂點的標記也要一起改變)。
- 重複 3 ,直到選夠 n - 1 條邊。
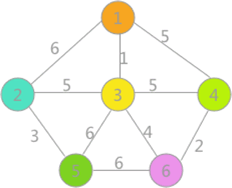
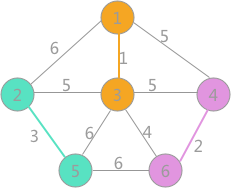
C 語言中文網:克魯斯卡爾演算法
有向無環圖 DAG
AOV 網
用頂點表示活動,邊表示活動的順序關係的有向圖。
AOV 網拓撲排序
方法:不停地輸出入度為 0 的頂點,輸出以後把頂點及其出弧刪掉,不斷重複。
程式結束時有兩種可能:
- 圖為空
- 圖中有環
逆拓撲排序:不停地輸出出度為 0 的頂點,輸出以後把頂點及其入弧刪掉,不斷重複。
如果確定圖中沒有環,可以採用 DFS 遍歷。
void Graph::checkLoop() {
int left(n); // 圖中剩餘頂點數
queue<int> nodeQue;
for (int i = 0; i < n; ++i) {
if (!InDegree[i]) {
nodeQue.push(i); // 將所有入度為 0 的頂點入佇列
}
}
while (!nodeQue.empty()) {
int front = nodeQue.front();
nodeQue.pop();
--left;
cout << front + 1 << " "; // 輸出頂點
for (int i = 0; i < n; ++i) {
if (adjMatrix[front][i]) {
--InDegree[i]; // 將鄰接點的入度 -1
if (!InDegree[i]) { // 若刪除頂點後鄰接點的入度變為 0
nodeQue.push(i); // 將鄰接點入對列
}
}
}
}
loop = left != 0;
}
C 語言中文網:拓撲排序演算法
AOE 網
用邊表示活動,用結點表示事件。
- 事件
- 在之前的活動已完成,在之後的活動可以開始。
- 源點
- 工程開始,是唯一入度為 0 的頂點。
- 匯點
- 工程結束,是唯一出度為 0 的頂點。
- 關鍵路徑
- 從源點到匯點最長路徑。其長度即為完成整個工程所需的時間。
- 關鍵活動
- 關鍵路徑上的活動。關鍵活動的時間餘量為 0。
只有在不改變關鍵路徑的情況下提高關鍵活動的速度才有效。
AOE 網求關鍵路徑
\(e(i)\):活動(邊)的最早開始時間。等於邊的起點的最早發生時間。
\(l(i)\):活動(邊)的最晚開始時間。等於邊的終點的最晚發生時間減去邊的權值。
\(Ve(i)\):事件(頂點)的最早發生時間。是從源點到該頂點的最長路徑長度。
一個事件只有等所有前提事件都完成後才能發生,因此其最早開始時間就是源點到該頂點的最長路徑長度。
\(Vl(i)\):事件(頂點)的最晚發生時間。是匯點的最早發生時間減去從匯點到該頂點的最長路徑長度。
如果一條邊的最早開始時間等於最晚開始時間,那麼這條邊所代表的活動就是關鍵活動。 求關鍵路徑問題就是求關鍵活動問題。
計算過程
- 源點的最早發生時間為 0 。
- 從已知最早發生時間的結點 \(v_i\) 出發,計算其直接後繼 \(v_j\) 的最早發生時間。其值等於 \(v_i\) 的最早發生時間加上 \(v_i\) 到 \(v_j\) 的最長路徑長度,並把計算中使用的最長路徑加粗。
- 重複 2 ,直到得到匯點的最早發生時間,即為整個工程的完成時間。關鍵路徑為所有加粗的路徑所形成的通路。
教材中使用的表格計演算法
int n; // 頂點數
int *InDegree; // 入度
int *Ve; // 頂點的最早發生時間
// 在拓撲排序的同時計算每個頂點的最早發生時間
int topoSort() {
int left = n; // 圖中剩下的頂點數
queue<int> nodeQue;
for (int i = 0; i < n; ++i) { // 將源點入佇列
if (!InDegree[i]) {
nodeQue.push(i);
Ve[i] = 0; // 源點的最早發生時間為 0
}
}
while (!nodeQue.empty()) {
int v = nodeQue.front();
nodeQue.pop(); // 不斷將入度為 0 的頂點出佇列
--left;
for (int i = 0; i < n; ++i) {
if (adjMatrix[v][i]) { // 找到 v 的鄰接點
--InDegree[i]; // 鄰接點的入度 -1
Ve[i] = max(Ve[i], Ve[v] + adjMatrix[v][i]); // 鄰接點的最早發生時間等於 v 的最早發生時間加上活動時間。當有多個 v 通往該鄰接點時,選取最大值。
if (!InDegree[i]) { // 若鄰接點入度變為 0 則入佇列
nodeQue.push(i);
}
}
}
}
if (left) { // 有剩餘頂點,說明圖中有環。
return -1;
} else {
return Ve[n - 1]; // 匯點的最早發生時間就是關鍵路徑的長度
}
}
最短路徑
Dijkstra 演算法
解決求出網中指定點到其餘各點的最短路徑長度的問題
將網中頂點分成 \(S\), \(U\) 兩組,\(S\) 為已求出最短路徑的頂點集合,初始時 \(S\) 中只有源點。\(U\) 包含其他頂點,且 \(U\) 中頂點的距離為源點鄰接該頂點的距離。以後每次都將路徑最短的頂點加入到 \(S\) 中,並重新整理最短路徑,直到所有頂點都加入到 \(S\) 中為止。
e.g.
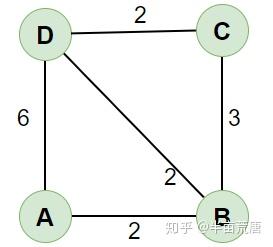
- 初始狀態,\(S=\{\,a(0)\,\},\ U=\{\,b(2),\,c(\infty),\,d(6)\,\}\)
- 取出最短路徑點 \(b(2)\),並以 \(b(2)\) 為橋樑重新整理與 \(b(2)\) 鄰接的點的距離。即 \(d_{ca}=\min\{\,l_{ca},\,l_{cb}+d_{ba}\,\}\)[1]
這裡 \(d_{ca}=\min\{\,\infty,\,2+3\,\}=5,\quad d_{da}=\min\{\,\infty,\,2+2\,\}=4\)
此時 \(S=\{\,a(0),\,b(2)\,\},\ U=\{\,c(5),\,d(4)\,\}\) - 重複 2
vector<int> *Graph::Dijkstra(int src) {
using d_v = pair<int, int>; // (d)v,最短路徑_頂點
priority_queue<d_v, vector<d_v>, greater<d_v>> min_heap; // 建立一個小頂堆(距離最近的頂點在堆頂),儲存已經確認可達的頂點 (d)v。每次將距離最短的頂點(堆頂)取出,用它來重新整理其鄰接點的最短路徑。
bool *flag = new bool[n]{}; // 用於判斷是否已經使用過某頂點來重新整理其鄰接點的最短路徑
vector<int> dist = new vector<int>(n, INF); // 所有頂點的最短路徑,初始化所有頂點的最短路徑為無窮大(不可達)。透過每次從堆頂取出的頂點(新確定最短路徑的頂點)來重新整理各頂點的最短路徑。
dist[src] = 0; // 源點的最短路徑為 0
min_heap.push(make_pair(0, src)); // 將源點插入小頂堆,使迴圈開始執行。
while (!min_heap.empty()) {
int u = min_heap.top().second; // 取出距離最近的頂點 u
min_heap.pop();
if (!flag[u]) {
for (auto i = adj[u].begin(); i != adj[u].end(); ++i) { // 以 u 為中轉站,重新整理其鄰接點的最短路徑。
int v = i->first; // u 的鄰接點 v
int weight = i->second; // 邊 (u, v) 的權
if (dist[v] > dist[u] + weight) { // 若透過 u 中轉可以縮短 (d)v
dist[v] = dist[u] + weight; // 更新 (d)v
min_heap.push(make_pair(dist[v], v)); // 將新的 (d)v 加入小頂堆
} // 因為我們可能將同一個頂點多次加入 min_heap,所以需要判斷之前是否已經使用過某個頂點。
}
flag[u] = true;
}
}
int max = 0;
for (int i = 0; i < n; ++i) {
max = dist[i] > max ? dist[i] : max;
}
return max;
}
CSDN:Dijkstra 演算法原理
知乎:Dijkstra 演算法詳解 通俗易懂
Floyd Warshall 演算法
解決求出網中任意兩點之間的最短路徑長度的問題
首先構造網的鄰接矩陣,這個鄰接矩陣同時表示網中任意兩頂點在不借助任何中轉頂點的情況下的最短路徑。
接下來,我們讓 \(v_0\) 作為中轉站,計算網中各頂點間的最短路徑。即對矩陣中每一項,令 d[i][j] = min(d[i][j], d[i][0] + d[0][j])。
此時的矩陣表示網中任意兩頂點在可以藉助 \(v_0\) 中轉的情況下的最短路徑。
接下來讓 \(v_1\) 作為中轉站,計算網中各頂點間的最短路徑 d[i][j] = min(d[i][j], d[i][1] + d[1][j]。
因為此時的 d[i][j],d[i][1] 和 d[1][j] 已經是在可以藉助 \(v_0\) 中轉的情況下的最短路徑了,所以這時得到的矩陣表示網中任意兩頂點在可以藉助 \(v_0\) 和 \(v_1\) 中轉的情況下的最短路徑。
如此重複 \(n\) 次,這時所有的頂點都可作為中轉站了,此時的矩陣就表示網中任意兩點間的最短路徑了。
記錄最短路徑
使用一個二維陣列 next[i][j] 記錄在 \(i\) 到 \(j\) 的最短路徑中,\(i\) 的下一個頂點是什麼。
初始時,若 \(v_i\), \(v_j\) 鄰接 graph[i][j] != INF,則 next[i][j] = j。
之後計算網中任意兩頂點在可以藉助 \(v_k\) 中轉的情況下的最短路徑,若發現將 \(v_k\) 新增進來後可以縮短 \(v_i\) 到 \(v_j\) 的最短路徑,那麼 \(v_i\) 到 \(v_j\) 的最短路徑的下一個頂點就應該是 \(v_i\) 到 \(v_k\) 的最短路徑的下一個頂點,即 next[i][j] = next[i][k]。
void Floyd() {
for (int k = 0; k < n; ++k) {
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (graph[i][j] > graph[i][k] + graph[k][j]) { // 如果透過 k 可以縮短 i, j 的長度
graph[i][j] = graph[i][k] + graph[k][j]; // 更新最短路徑長度
next[i][j] = next[i][k]; // 從 i 到 j 的最短路徑的下一個頂點就是從 i 到 k 的最短路徑的下一個頂點
}
}
}
}
}
知乎:弗洛伊德演算法
查詢
平均查詢長度(ASL)
- \(p_i\) 是查詢到某個元素的機率
- \(c_i\) 是查詢到這個元素時已經比較的次數
若假定每個結點被查詢的機率相同,即 \(p_i=\dfrac{1}{n}\),則:
幾種常見的平均查詢長度
順序查詢
二分查詢
\(l\) :層數;
\(k\) :該層的結點數
二分查詢判定樹中的結點都是查詢成功的情況。為每個結點的空指標建立一個實際上不存在的結點——外結點,所有外結點都是查詢不成功的情況。如果有序表的長度為 \(n\),則外結點一定有 \(n + 1\) 個。
深度為 \(h\) 的滿二叉樹的結點數為 \(2^h-1\),第 \(i\) 層的結點數為 \(2^{i-1}\)
\({\rm ASL}_{平均}\) 是滿二叉樹的平均查詢長度
部落格園:如何計算折半查詢的平均查詢長度?
二叉排序樹
樹中結點的比較次數就是結點的層數
- \(l_i\) 是層數
- \(k_i\) 是該層的結點數
雜湊表
開放定址法
\(m\) 是 \(H(key)\) 值域的長度
開放定址法中與 NULL 的比較也算次數(因為不知道下一個元素是不是 NULL),而鏈地址法不算與 NULL 的比較次數。
鏈地址法
CSDN:常見的平均查詢長度總結
靜態查詢表
二分查詢
C 語言中文網:二分查詢
分塊查詢
C 語言中文網:分塊查詢
動態查詢表
若找到關鍵字,則返回其指標。否則建立關鍵字並返回其指標。
二叉排序樹
C 語言中文網:二叉排序樹
初始時為空樹。在查詢時,若查詢關鍵字比結點關鍵字小,則在其左子樹中查詢,否則在右子樹中查詢。若左(右)子樹為空,則以關鍵字建立左(右)子樹。
刪除結點
若結點 P 只有左子樹或右子樹,則摘除 P,然後把左子樹或右子樹順移上來即可。
若 P 既有左子樹,又有右子樹,此時有兩種方法:
- 令結點 P 的左子樹為 P 的父結點的左子樹;結點 P 的右子樹為 P 的直接前驅的右子樹。(把 P 的右子樹接到 S 上,變成 S 的右子樹)
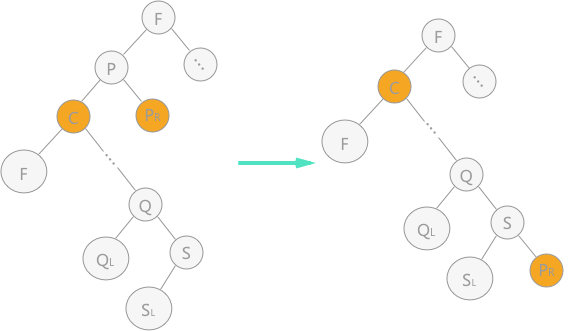
P 的左子樹是所有比 P 小的結點,P 的右子樹是所有比 P 大的結點,因此刪除 P 後,P 的右子樹比 P 的左子樹的所有結點都大,可以作為左子樹最右下的結點(即 P 的直接前驅)的右子樹。
- 用結點 P 的直接前驅(或直接後繼)S 來代替結點 P,同時在二叉排序樹中對 S 做刪除操作。(用 S 替代 P)
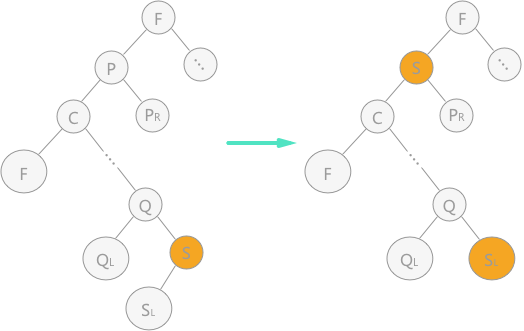
P 的直接前驅 S 就是 P 的左子樹中最大的結點(最大的比 P 小的結點),因此如果用 S 代替 P,S 的左子樹依然是所有比 S 小的結點,S 的右子樹依然是所有比 S 大的結點。
P 的直接前驅是 P 的左子樹中最右下的結點,因此它或者是葉子結點,或者只有左子樹。因此對 S 的刪除操作只要摘除 S,並將 S 的左子樹(如果有的話)順移上來即可。
直接後繼 Q 是右子樹中最小的結點,如果用 Q 代替 P,那麼 Q 的左子樹依然都比 Q 小,Q 的右子樹依然都比 Q 大。
void delete(Node *&node) {
if (!node->rchile) { // 若沒有右孩子
Node *temp = node;
node = node->lchild;
delete temp;
} else if (!node->lchild) { // 有右孩子但沒有左孩子
Node *temp = node;
node = node->rchild;
delete temp;
} else { // 左右孩子都有
Node *pre = node->lchild; // node 的直接前驅
Node *pre_parent = node; // pre 的父節點
while (pre->rchild) { // node 的直接前驅是其左子樹最右下的結點
pre_parent = pre;
pre = pre->rchild;
}
node->val = pre->val; // 用直接前驅的值替換刪除結點的值
// 接下來要刪除直接前驅
if (pre_parent != node) { // 如果 node 的左孩子有右孩子(即直接前驅不是 node 的左孩子)
pre_parent->rchild = pre->lchild;
} else { // 如果 node 的左孩子沒有右孩子(即直接前驅就是 node 的左孩子)
pre_parent->lchild = pre.lchild;
}
delete pre;
}
}
平衡二叉樹
- 平衡因子(BF)
- 左子樹的深度減去右子樹的深度
- 若二叉樹中所有結點的平衡因子的絕對值都不超過 1 ,則該樹稱為平衡二叉樹。
- 最小不平衡子樹
- 從新插入的結點開始向上查詢,以第一個平衡因子的絕對值超過 1 的結點為根的子樹稱為最小不平衡子樹。
- 平衡二叉樹的失衡調整主要是透過旋轉最小失衡子樹來實現的。旋轉的目的就是減少高度,透過降低整棵樹的高度來平衡。哪邊的子樹高,就把哪邊的子樹向上旋轉。
左旋
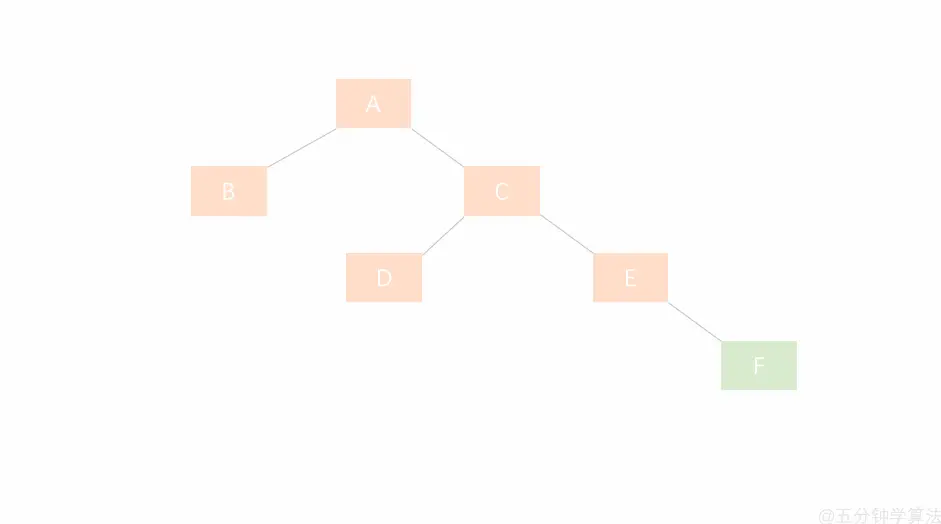
- 讓根結點的右孩子作為新根
- 新根的左孩子作為舊根的右孩子
- 舊根作為新根的左孩子
右旋

- 讓根結點的左孩子作為新根
- 新根的右孩子作為舊根的左孩子
- 舊根作為新根的右孩子
先左後右
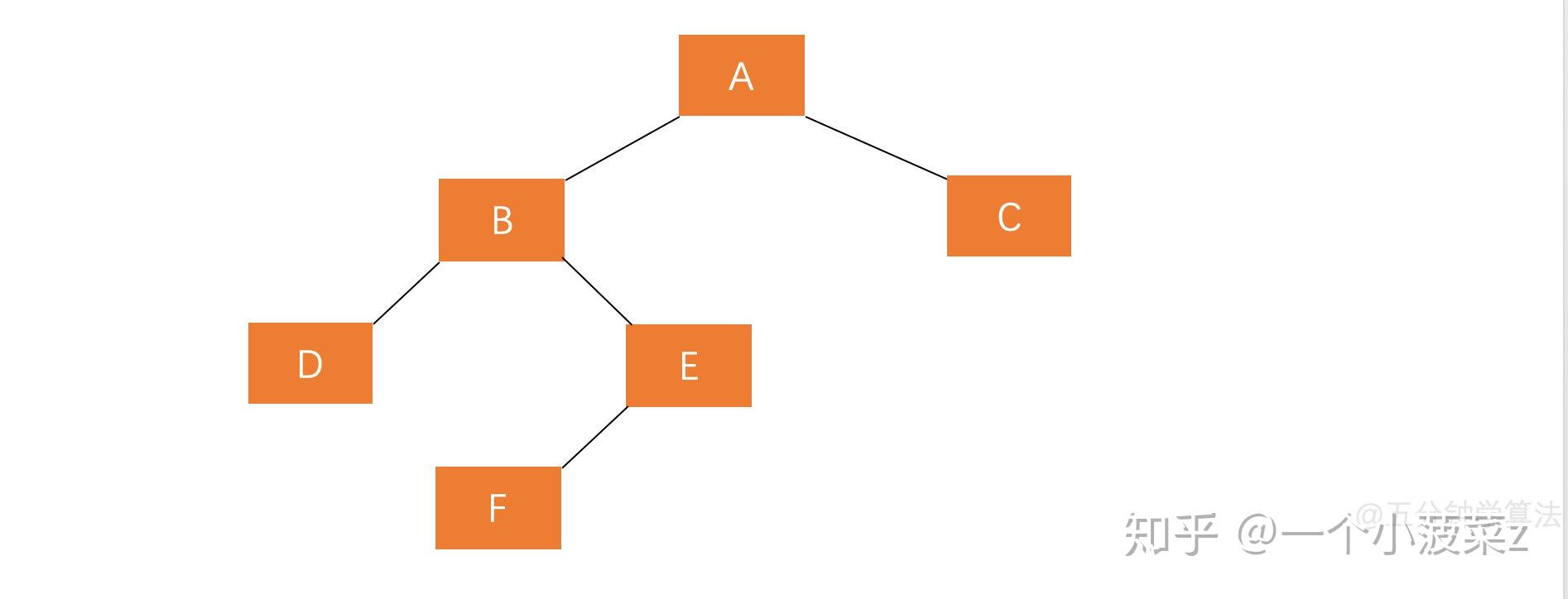
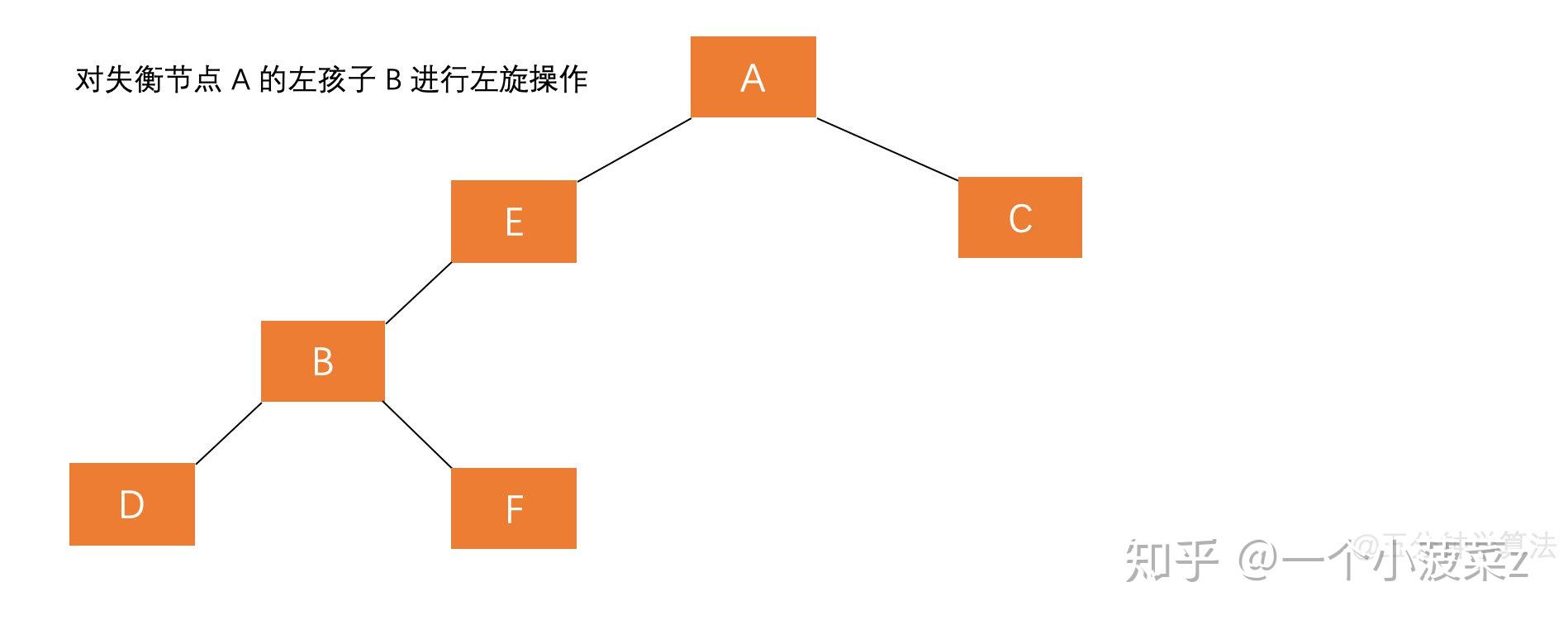
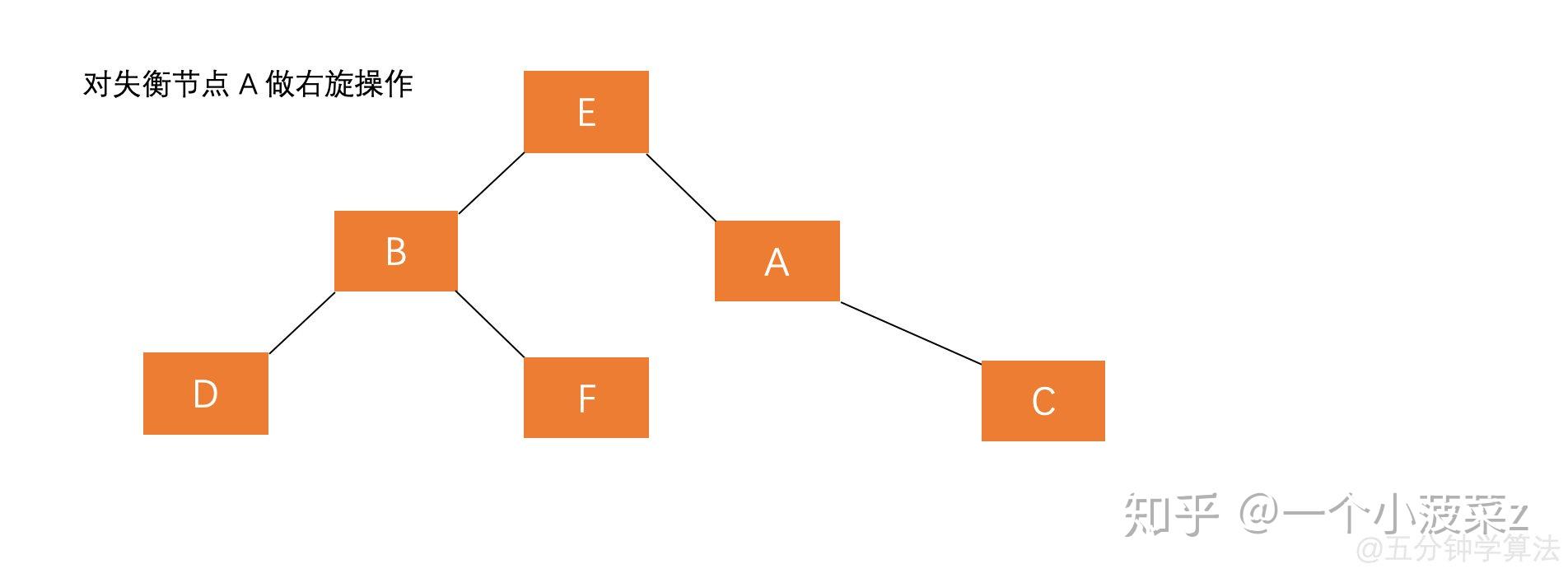
四種可能的失衡方式及解決方法
| 插入方式 | 描述 | 旋轉方式 |
|---|---|---|
| LL | 在 A 的左孩子的左子樹上插入結點而破壞平衡 | 右旋 |
| RR | 在 A 的右孩子的右子樹上插入結點而破壞平衡 | 左旋 |
| LR | 在 A 的左孩子的右子樹上插入結點而破壞平衡 | 先左旋後右旋 |
| RL | 在 A 的右孩子的左子樹上插入結點而破壞平衡 | 先右旋後左旋 |
知乎:什麼是平衡二叉樹(AVL)
B-樹
C 語言中文網:B-樹及其基本操作詳解
用於檔案存放
- m 階 B-樹
- 每個結點至多有 m 棵子樹
- 若根結點不是葉子結點,則至少有兩棵子樹
- 除根之外的所有非終端結點至少有 \(\lceil m/2\rceil\) 棵子樹
- B-樹的葉子結點都是 NULL 結點,並都在同一層次
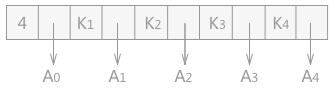
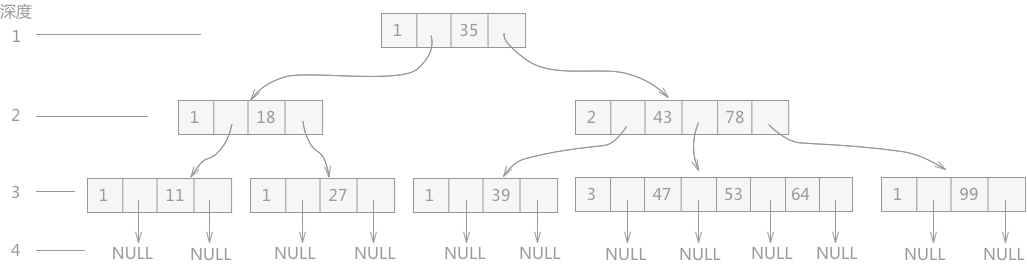
插入關鍵字
因為對於 \(m\) 階的 B-樹來說,所有的非終端結點包含關鍵字的個數的範圍是[⌈m/2⌉-1, m-1],所以在插入新的資料元素時,首先向最底層的某個非終端結點中新增,如果該結點中的關鍵字個數沒有超過 \(m-1\),則直接插入成功,否則還需要繼續對該結點進行處理。
分裂:
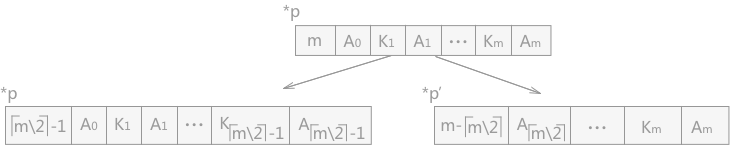
自己只保留 ⌈m/2⌉-1 個關鍵字,把第 ⌈m/2⌉ 個關鍵字放到父結點中,並且該關鍵字右側的指標指向剩下的關鍵字組成的結點。
刪除關鍵字
兩種情況:
- 刪除最後一層結點
- 刪除其餘結點
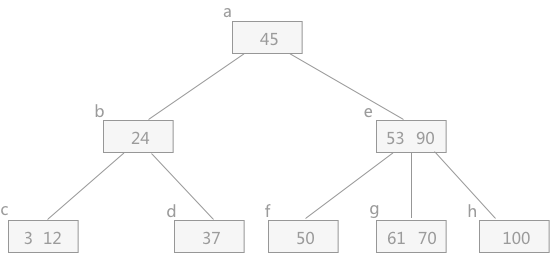
刪除其餘結點:只需找到該結點
雜湊表
雜湊函式的構造
直接定址法
\(H(key)=a\cdot key+b\)
數字分析法
當關鍵字由多位字元或數字組成,就可以抽取其中的 2 位或多位作為雜湊地址。
雜湊地址表示關鍵字在查詢表中的儲存位置,而不是實際的實體地址
平方取中法
對關鍵字做平方操作,取中間幾位作為雜湊地址。
摺疊法
將關鍵字分割成位數相同的幾部分(最後一部分的位數可以不同),然後取這幾部分的疊加和(捨去進位)作為雜湊地址。
- 移位摺疊
- 間界摺疊

除留餘數法(常用)
\(H(key)=key\,\%\,p\)
\(p\) 通常取不大於表長且最接近表長的質數或不包含小於 20 的質因子的合數。
偽隨機數法
\(H(key)=\text{rand}(key)\)
適用於關鍵字長度不等的情況。
處理衝突的方法
開放定址法
\(H(key)=\left(H(key)+d\right)\%\,m\)
\(m\) 為表長
獲取 \(d\) 的值:
- 線性探測法 \(d_i=1,2,3,\ldots\)
- 二次探測法 \(d_i=1^2,-1^2,2^2,-2^2,\ldots\)
- 偽隨機數探測法
線性探測法就是一個一個往後找,找到空位置就放進去
線性探測法容易產生堆積的問題:幾個雜湊地址不同的關鍵字爭奪同一個雜湊地址
再雜湊法
當透過雜湊函式求得的雜湊地址衝突時,使用另一個雜湊函式計算,直到沒有衝突為止。
鏈地址法
將所有產生衝突的關鍵字儲存到一個連結串列中。
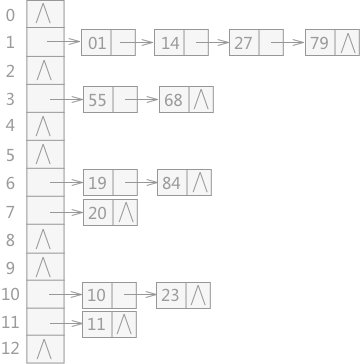
建立公共溢位區法
建立兩張表,一張基本表,一張溢位表。基本表儲存沒有衝突的資料,溢位表儲存有衝突的資料。
排序
插入排序
將表分為有序表和無序表兩段。首先將表中第一個元素加入有序表,之後每次取無序表第一個元素,將其與有序表尾元素比較,若大於等於則直接放在有序表後面,有序表長度加一。否則進入有序表查詢,找到合適的位置後將該位置及之後的有序表元素後移一位,然後將該元素插入,有序表長度加一。不斷重複,直到有序表長度等於原表長。

void insertSort(long arr[], int size) {
for (int i = 1; i < size; ++i) { // i 代表無序表的起始位置
long temp = arr[i]; // 記錄待插入元素的值
int j = i - 1; // 接下來即將比較元素的索引
while (j > -1 && temp < arr[j]) { // 查詢插入位置,同時將有序表元素後移。
arr[j + 1] = arr[j];
--j;
}
arr[j + 1] = temp; // 此時 temp 大於等於元素 j,將 temp 插入到 j 後面。
}
}
折半插入排序
在查詢的過程中,由於是在有序表中查詢,因此可以使用折半查詢法。
void insertSort(int arr[], int size) {
int beg, end; // [beg, end)
for (int i = 1; i < size; ++i) {
beg = 0;
end = i;
int temp = arr[i];
while (beg < end) {
int mid = (beg + end) / 2;
if (temp < arr[mid]) {
end = mid;
} else {
beg = mid + 1;
}
}
for (int j = i - 1; j >= beg; --j) { // 有序表中插入位置後的元素統一後移
arr[j + 1] = arr[j];
}
arr[beg] = temp; // 插入元素
}
}
二路插入排序
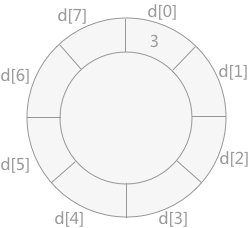
在插入排序中,一大消耗時間的操作就是將有序表中的元素後移的過程。當需要將元素插入到表頭位置時,需要將有序表中的所有元素後移一位。如果我們可以直接將元素放到有序表前面,那麼就能省下移動元素的時間。利用迴圈陣列可以達到這一效果。
void insertSort(long arr[], int size) {
long circ[size]; // 迴圈陣列
int front, back; // 迴圈陣列的首和尾
front = back = 0;
circ[0] = arr[0];
for (int i = 1; i < size; ++i) {
if (arr[i] < circ[front]) { // 待插入元素比迴圈陣列首元素小,插入到迴圈陣列首。
front = (front - 1 + size) % size;
circ[front] = arr[i];
} else if (arr[i] > circ[back]) { // 待插入元素比迴圈陣列尾元素大,插入到迴圈陣列尾。
back = (back + 1 + size) % size;
circ[back] = arr[i];
} else { // 其他情況
int j = back;
while (arr[i] < circ[j]) { // 查詢插入位置並後移陣列元素
circ[(j + 1 + size) % size] = circ[j];
j = (j - 1 + size) % size;
}
circ[(j + 1 + size) % size] = arr[i]; // 插入
back = (back + 1 + size) % size;
}
}
for (int i = 0; i < size; ++i) { // 將迴圈陣列複製到原表中
arr[i] = circ[(front + i + size) % size];
}
}
表插入排序
前面的三種插入排序演算法都使用陣列進行儲存,無法避免排序過程中的資料移動問題。要想從根本上解決問題只能改變儲存結構,即使用(迴圈)連結串列。

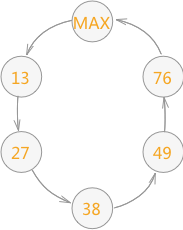
對連結串列進行再加工
表插入排序演算法得到的有序表是用連結串列表示的,意味著在使用時只能使用順序查詢。為了使用時更高效,我們可以將它轉換成陣列。
具體方法是:找到連結串列第一個結點,先儲存它的地址 cur 和連結串列下一個結點的地址 next,然後將它與陣列第一個元素互換位置,同時將它的 next 指向原地址 cur,方便我們之後找到與它互換位置的元素。然後透過 next 移到下一個元素,重複。

找到首結點 list[4]13,儲存 cur = 4,next(圖中是 p) = 5。將它與 list[1] 互換,然後將它的 next 值置為 4
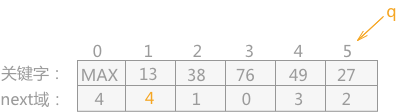
透過 next 找到第二個結點 list[5]27,儲存 cur = 5,next = 2。將它與 list[2] 互換位置,然後將它的 next 值置為 5。
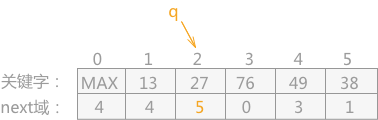
透過 next 找到第三個結點 list[2]27,此時我們已經將下標 3 之前的所有元素互換過位置,因此此時的 list[2] 已經不是原先的元素了,需要透過它的 next 指標找到原先的元素,即 list[5]38。儲存 cur = 5,next = 1。將它與 list[3] 互換位置,然後將它的 next 置為 5。
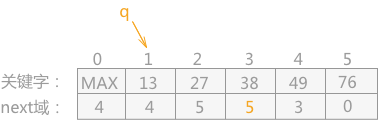
透過 next 找到第四個結點 list[1],同樣,需要再透過它的 next 指標找到原先的元素 list[4]。list[4] 就在第四個位置上,它的位置不用改變。接下來的 list[5] 的位置也不用改變,排序完成。
class Node {
int val;
int next;
}
class LinkList {
Node list[SIZE];
int length;
}
void rearrange(LinkList &l) { // 將有序連結串列轉換成有序陣列
int cur = l.list[0].next; // 定位到首結點
for (int i = 1; i < l.length; ++i) { // i 之前的元素都是重新排列過的
if (cur < i) { // 需要找到原先的元素
cur = l.list[cur].next;
}
int next = l.list[cur].next;
if (cur != i) {
swap(l.list[i], l.list[cur]);
l.list[i].next = cur;
}
cur = next;
}
}
希爾排序
簡書:希爾排序
快速排序
快速排序演算法是在起泡排序的基礎上進行改進的一種演算法,其實現的基本思想是:透過一次排序將整個無序表分成相互獨立的兩部分,其中一部分中的資料都比另一部分中包含的資料的值小,然後繼續沿用此方法分別對兩部分進行同樣的操作,直到每一個小部分不可再分,所得到的整個序列就成為了有序序列。
例如,對無序表 { 49, 38, 65, 97, 76, 13, 27, 49 } 進行快速排序,大致過程為:
- 選取表中第一個元素作為支點,選取 49
- 將表格中小於 49 的元素放在 49 的左側,大於 49 的放在 49 的右側。完成後的無序表為:
{ 27, 38, 13, 49, 65, 97, 76, 49 } - 以 49 為支點將整個無序表分割成了兩個部分,分別為
{ 27, 38, 13 }和{ 65, 97, 76, 49 },繼續採用此方法分別對兩個子表進行排序 - 前部分子表以 27 為支點,排序後的子表為
{ 13, 27, 38 },此部分已經有序;後部分子表以 65 為支點,排序後的子表為{ 49, 65, 97, 76 } - 此時前半部分子表中的資料已完成排序;後部分子表繼續以 65 為支點,將其分割為
{ 49 }和{ 97, 76 },前者不需排序,後者排序後的結果為{ 76, 97 } - 透過以上幾步的排序,最後由子表
{ 13, 27, 38 }、{ 49 }、{ 49 }、{ 65 }、{ 76,97 }構成有序表:{ 13, 27, 38, 49, 49, 65, 76, 97 }
其中最重要的步驟是透過支點分割無序表的操作。具體方法是:建立兩個指標 low 和 high,分別指向無序表的首和尾。首先將支點即 arr[low] 取出來,這時 low 指向的位置為空。保持 low 不動,不斷將 high 左移,直到找到比支點小的元素,然後將該元素拋給 low。此時 high 所指向的位置為空。保持 high 不動,不斷將 low 右移,直到找到比支點大的元素,再拋給 high。重複,直到 low 和 high 重合。此時它們指向的位置的元素已經被 low 或 high 丟擲去了,並且該位置的左邊都是比支點小的元素,該位置的右邊都是比支點大的元素。將支點插入該位置,此時就完成了分割操作。
// 將無序表 [low, high] 以 arr[low] 為支點分為兩部分。返回支點索引。
int partition(int arr[], int low, int high) {
int pivot = arr[low]; // 取出支點
while (low < high) {
while (low < high && arr[high] >= pivot) { // 不斷將 high 左移,直到找到比支點小的元素。
--high;
}
arr[low] = arr[high]; // 將該元素拋給 low
while (low < high && arr[low] <= pivot) { // low 指標右移,直至遇到比支點大的元素。
++low;
}
arr[high] = arr[low]; // 將該元素拋給 high
}
arr[low] = pivot; // 放回支點
return low;
}
void quickSort(int arr[], int low, int high) {
if (low < high) {
int pivotLoc = partition(arr, low, high); // 將無序表分割成兩個子表
quickSort(arr, low, pivotLoc - 1); // 對支點左側的子表進行排序
quickSort(arr, pivotLoc + 1, high); // 對支點右側的子表進行排序
}
}
堆排序
- 堆
- 一般指二叉堆,二叉堆是完全二叉樹(葉子結點只能出現在最下層和次下層,且最下層的葉子結點集中在樹的左部)。
- 大頂堆:父結點大於等於子結點
- 小頂堆:父結點小於等於子結點
堆排序的基本思想是:將無序序列構造成一個大頂堆,此時整個序列的最大值就是堆頂,將其與堆尾交換,然後將堆尾摘除,放在陣列末尾。然後將剩餘 \(n-1\) 個元素重新構造成一個大頂堆。如此反覆執行,便能得到一個有序序列了。
堆尾指的是堆裡下標最大的結點
在構造大頂堆的過程中,由於大頂堆不僅要求根結點大於等於其左右孩子,還要求以左右孩子為根的子樹本身也是大頂堆。因此必須自底向上,從最後一個根結點開始構建大頂堆。(上浮)
交換堆頂與堆尾的操作會破壞堆的結構,因此交換堆頂與堆尾之後還需要自上向下重新構建大頂堆。(下沉)
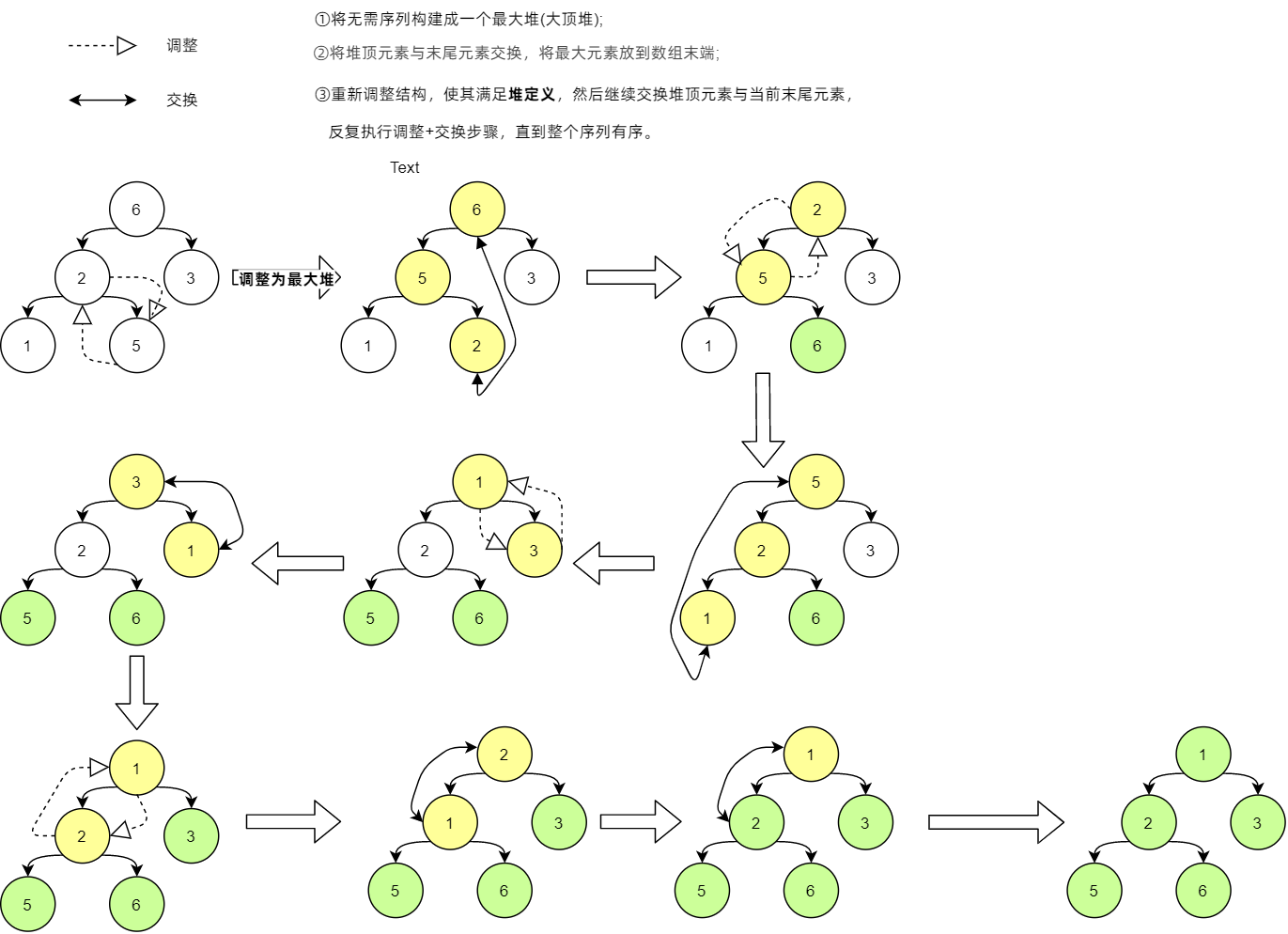
// 堆化以 root 作為根結點的子樹。arr 是排序陣列,n 是元素個數。
void heapify(int arr[], int n, int root) {
int largest = root; // 將最大結點初始化為根結點
int lChild = 2 * root + 1;
int rChild = 2 * root + 2;
if (lChild < n && arr[lChild] > arr[largest]) { // 用左孩子更新最大結點
largest = lChild;
}
if (rChild < n && arr[rChild] > arr[largest]) { // 用右孩子更新最大結點
largest = rChild;
}
// 如果最大結點不是根結點,就交換最大結點和根結點的值。
if (largest != root) {
swap(arr[root], arr[largest]);
heapify(arr, n, largest); // 交換操作可能破壞子堆的結構,因此重新堆化子堆。
}
}
// 堆排序主函式
void heapSort(int arr[], int n){
for (int i = n / 2 - 1; i >= 0; --i) { // 自底向上構建堆
heapify(arr, n, i);
}
// 一個一個地從堆頂提取元素
for (int i = n - 1; i > 0; --i) {
swap(arr[0], arr[i]); // 將堆頂與堆尾交換
heapify(arr, i, 0); // 堆頂與堆尾交換破壞了子堆的結構,重新堆化子堆。
}
}
陣列的最後一個結點的索引是 \(n-1\),設其父結點的索引為 \(i\),則有:
- 若該結點是 \(i\) 的左孩子,則 \(2i + 1 = n - 1\),解得 \(i = n / 2 - 1\) ( \(n\) 為偶數);
- 若該結點是 \(i\) 的右孩子,則 \(2i + 2 = n - 1\),解得 \(i = (n - 1) / 2 - 1\) ( n 為奇數) = \(n / 2 - 1\);
所以,最後一個根結點的索引永遠是 \(n / 2 - 1\) 。
歸併排序
CSDN:歸併排序
計數排序
知乎:計數排序
桶排序
C 語言中文網:桶排序
基數排序
C 語言中文網:基數排序
(\(d\) 指兩點間的最短路徑長度,\(l\) 指兩點間的鄰接距離) ↩︎