若無特殊說明,以下所有圖均指連通圖。
定義
尤拉路徑,尤拉回路,尤拉圖
對於一個圖,如果存在一條路徑恰好經過所有邊一次,則稱這條路徑為一條尤拉路徑。
如果存在一條迴路經過所有邊恰好一次,則稱這條路徑為一條尤拉回路。
存在尤拉回路的圖被稱為尤拉圖。
環分解
如果一個圖的邊集可以被分成若干個簡單環,則稱這個圖可以環分解。
判定
判定定理1:一個圖存在尤拉回路當且僅當這個圖可以被環分解。
- 充分性:如果可以環分解,那麼每次選取兩個相交的環合併成一個大環即可。
- 必要性:對於一條尤拉回路,每次遇到重複點就把這段路徑連成的環分解出去,這樣一定能形成若干簡單環。
判定定理2:一個圖可以被環分解當且僅當所有點度數都為偶數。
- 充分性:每次選取一個簡單環,刪掉之後所有點度數依舊是偶數,歸納即可。
- 必要性:每個點進入次數和出去次數相等,因此都是偶數。
結合上面兩條我們可以得出尤拉回路的判定定理:
判定定理3:一個圖存在尤拉回路當且僅當所有點度數都是偶數。
並且我們可以知道,一個圖存在尤拉回路、可以被環分解、所有點度數都是偶數,這是三個完全等價的條件。
對於有向圖,類似的可以得出充要條件是所有節點入度等於出度。
還有下面的推論:
推論:一個圖存在尤拉路徑當且僅當恰好有兩個結點的度數是奇數。
求法
Hierholzer 演算法
維護當前的尤拉回路,每次把迴路裡的一個點擴充成一個環。
DFS 寫法
核心思路是每次找環拼起來,實際上有一個簡單的 DFS 做法:從任意一個節點開始,每次列舉當前點的出邊,沿著第一個沒有走的走過去,程式碼如下:
void dfs(int x)
{
for(int i=0;i<G[x].size();i++)if(!vis[G[x][i].id])
{
vis[G[x][i].id]=1;
int y=G[x][i].y;
dfs(y);
}
ans[++tot]=x;//回溯的時候再把點加進去
}
為什麼要在回溯的時候才加點?
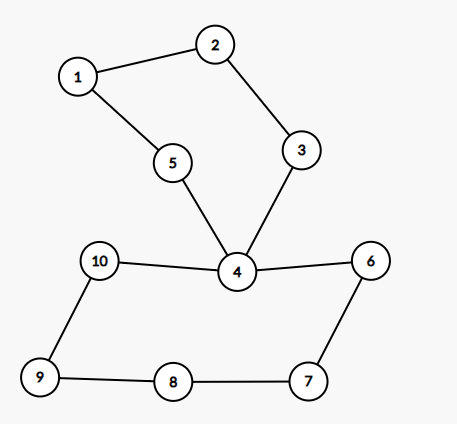
如圖所示,我們以 \(1\) 號點為起點,沿著 1 - 5 - 4 - 3 - 2 -1 找到一個環,但是如果直接按照 DFS 訪問順序加點,另一個環就訪問不到了;而在回溯時加點就可以避免這個問題,如果回溯過程中找到了新的環就可以直接加到尤拉回路里。
不過因為是回溯過程加的點,所以最後求的是倒著的一條尤拉回路,我們反過來輸出即可。
對於尤拉路徑,只要從度數為奇數的點開始 DFS 就行了。
當前弧最佳化
按照上面的程式碼寫複雜度是不對的,因為每次都要重新列舉所有出邊,不過顯然可以記錄一個變數表示當前遍歷到每個節點的哪條出邊,這樣接著這個變數繼續列舉即可,程式碼如下:
void dfs(int x)
{
for(int &i=cur[x];i<G[x].size();i++)if(!vis[G[x][i].id])
{
vis[G[x][i].id]=1;
int y=G[x][i].y;
dfs(y);
}
ans[++tot]=x;//回溯的時候再把點加進去
}
最小字典序尤拉回路
把每個節點的出邊按照字典序排序即可。
基礎題目
P7771 【模板】尤拉路徑
[USACO3.3] 騎馬修柵欄 Riding the Fences
上面兩道都是模板題。
[ABC286G] Unique Walk
因為非關鍵邊可以經過任意次,所以直接把非關鍵邊連線的點縮成來,在剩下的圖上跑尤拉回路即可。
BZOJ3706 反色刷
首先有解的條件顯然是所有點連的黑色邊數量都是偶數。
對於一個有至少一條黑色邊的連通塊,一定只需要一次操作就能全變白,因此答案就是有至少一條黑色邊的連通塊數量。
CF723E One-Way Reform
首先答案最多是度數為偶數的點的個數,並且我們可以達成這個上界:
新建一個虛點,從虛點向每個度數為奇數的點連邊,然後跑一條尤拉回路,按照尤拉回路的方式定即可。
CF547D Mike and Fish
對行列建點,建成一個二分圖,然後每個點在他對應的行列之間連邊。
延續上一個題的構造就可以把每條邊定向使得所有點的入度和出度差的絕對值不超過 \(1\)。
CF209C Trails and Glades
如果圖連通,那麼答案肯定是奇數點個數/2。
如果圖不連通,那麼對於一個沒有奇數點的連通塊,向外面連兩條出邊即可。
進階題目
CF429E Points and Segments
如果區間是紅色就給區間內的點都加一,否則都減一,最後要求所有點的絕對值不超過 \(1\)。
考慮如果所有點都偶數個區間覆蓋時,我們這樣構造:
對於每個區間,在 \(l,r+1\) 之間連無向邊,然後跑尤拉回路,如果這條邊從左指向右就讓差分陣列 \(d_l-1,d_{r+1}+1\),另一種類似。這樣因為每個點入度出度相等,所以差分陣列 \(d_i=0\),故所有點被兩種區間覆蓋的次數都相等,符合條件。
當有些點被覆蓋奇數次時,類似之間加虛點的操作,我們對於每個被覆蓋奇數次的位置 \(x\),加入一個區間 \([x,x]\) ,再跑上面的做法即可。
[IOI2016] railroad
題意就是,你在數軸上游走,向左走代價為 \(1\),向右走沒有代價,還有 \(m\) 條有向特殊邊必須經過恰好一次,問最優代價。
考慮最終你遊走的過程,如果 \(i\to i+1\) 走了 \(c\) 次,就連 \(c\) 條 \(i\to i+1\) 的邊,\(i+1\to i\) 同理,那麼就是要求加最少代價的邊使得存在尤拉路徑。
路徑是不太好處理的,注意到我們可以加一條 \(inf\) 到 \(1\) 的邊不影響答案,因此可以變成詢問尤拉回路。
對於相鄰兩條邊 \(i\to i+1\),我們求出它被特殊邊覆蓋的次數(從右向左是-1,從左向右是+1) \(w\),如果 \(w>0\),我們需要再加入 \(w\) 條向 \(i+1\to i\) 的邊,代價為 \(w\),否則假如 \(i\to i+1\) 的邊,不需要代價。
這樣加邊顯然是最優的,並且滿足了尤拉回路的一個限制:所有點度數都是偶數。
但是還要聯通才能有尤拉回路,於是我們還要加一些邊使得圖聯通,顯然只會加在相鄰兩點之間,一去一來。然後我們把這些邊跑一個最小生成樹使得圖聯通即可。
[省選聯考 2020 B 卷] 丁香之路
和上題大致相同,只是向左向右都有代價了,沒有什麼本質區別。
CF325E The Red Button
首先容易證明 \(n\) 為奇數無解,否則令 \(m=n/2\) 。
關鍵性質,\(x,x+m\) 擁有相同的入邊,出邊集合,其中 \(x\in [0,m)\) 。也就是說這對點某種程度上可以看成一個點
那麼我們建一個 \(m\) 個點的圖,每個點實際代表一對點 \([0,m)\) 。然後從 \(x\) 向 \(2x\bmod m,2x+1\bmod m\) 連邊跑尤拉回路,正確性證明比較顯然。