機率圖模型基礎

1. 概念

機率：機率模型關心的是一個多維的機率分佈

圖：即圖論的圖，起的作用為一個工具，直觀表達機率之間的聯絡，將機率嵌入圖中，使得模型更加直觀，可以將機率模型的特徵明顯表示出來。

對於多維隨機變數\(p(x_1, \dots, x_p)\), 常用計算為求邊緣機率與條件機率，即有如下運算

1. Sum Rule
   \[p(x_1) = \int_{x_2} \dots \int_{x_p} p(x_1, \dots, x_p) dx_2 \dots dx_p \]

2. Product Rule
   \[p(x_1|x_2) = \frac{p(x_1, x_2)}{p(x_2)} \]

3. Chain Rule
   \[p(x_1, \dots, x_p) = p(x_1) p(x_2|x_1) \dots p(x_p|x_1, \dots, x_{p-1}) \]

4. Bayes' Rule
   \[p(x_1|x_2) = \frac{p(x_2|x_1)p(x_1)}{p(x_2)} = \frac{p(x_2|x_1)p(x_1)}{\int p(x_2|x_1)p(x_1)dx_1} \]

困境：對於多維隨機變數，計算\(p(x_1, \dots, x_p)\)計算量太大，要簡化計算

簡化 1：每個隨機變數之間相互獨立，即有\(p(x_1, \dots, x_p) = \prod_{i=1}^{p} p(x_i)\)

• Naive Bayes 假設所有特徵之間條件獨立，即有\(p(x_1, \dots, x_p|y) = \prod_{i=1}^{p} p(x_i|y)\)

簡化 2（Markov Property）：給定當前狀態，未來狀態與過去狀態無關，即有\(p(x_k | x_1, \dots x_{k-1},x_{k+1},\dots, x_{p}) = p(x_k | x_{k-1})\)

• HMM 隱馬爾科夫模型，使用齊次馬爾可夫假設

簡化 3（條件獨立性假設）：給定隱變數，觀測變數之間相互獨立，即有\(p(x_1, \dots, x_p|z) = \prod_{i=1}^{p} p(x_i|z)\)，是馬爾可夫性質的推廣

• Representation
  • 有向圖 Bayesian Network
  • 無向圖 Markov Network
  • 高斯圖 Gaussian Network(BN MN)
• Inference(給定已知資料，求另外的機率分佈)
  • Exact Inference：使用 DP 計算聯合分佈
  • Approximate Inference
    • 確定性近似（變分推斷）
    • 隨機近似 MCMC
• Learning
  • Parameter Learning
    • 完備資料
    • 隱變數
  • Structure Learning

2. Bayesian Network（有向圖模型）

使用條件獨立性，將聯合機率分解為多個條件機率的乘積，即有

\[p(x_1, \dots, x_p) = p(x_1)\prod_{i=2}^{p} p(x_i | x_{i-1}) \]

因子分解

構建圖，使用Topological Order，若有\(X \rightarrow Y\)，則有\(p(Y|X)\)，那麼從圖上即可以得到聯合機率分佈。

Local Structure

注意，接下來的情況是規律，是從圖與機率的關係得出的。

1. tail to tail
   若有三個隨機變數\(A, B, C\)滿足 chain rule，即\(p(A,B.C) = p(A) p(B|A) p(C|A,B)\)，同時有如下圖

graph TD A --> B A --> C

根據圖寫出關係，有\(p(A,B,C) = p(A) p(B|A) p(C|A)\)
則有\(p(C|A,B) = p(C|A)\)，其中\(p(C|A,B) = \frac{p(B,C|A)}{P(B|A)}\)
表明\(C\)與\(B\)條件獨立。

2. head to tail

graph LR A --> B B --> C

\(A\) 與 \(C\) 在 \(B\) 條件下獨立，即\(p(C|A,B) = p(C|B)\)

3. head to head

graph TD A --> C B --> C

預設情況下，\(A\) 獨立於 \(B\)
若\(C\)被觀測，\(A\) 與 \(B\) 有關係。

\[p(A,B,C) = p(A) p(B) p(C|A,B) = p(A) p(B|A) p(C|A,B) \]

可得預設情況下，\(A\) 與 \(B\) 獨立。

Representation: D - Separation

在圖中判斷節點集合的條件獨立性，使用 D-separation 規則。

graph TD A B C

D-separation 有兩個規則

1. 若有節點\(x_b\)作為跨點連線\(A\)與\(C\)，並形成 head to tail 或者 tail to tail 結構，那麼\(x_b\) 一定在\(B\)集合中
2. 若有節點\(x_b\)作為跨點連線\(A\)與\(C\)，並形成 head to head 結構，那麼\(x_b\) 一定不在\(B\)集合中

依次檢測所有跨點，若都滿足，那麼\(A\) 與 \(C\) 條件獨立。

這種判斷規則也叫全域性馬爾可夫性。

Representation: Sample

graph LR id1(Bayesian Network) --> id2(單一:NaiveBayes) id1 --> id3(混合:GMM) id1 --> id4(時間) id4 --> id5(Markov Chain) id4 --> id6(Gaussion Process 無限維高斯分佈) id1 --> id7(連續: Gaussian Network) id3 --> id8(動態模型) id4 --> id8 id8 --> id9(HMM:離散) id8 --> id10(Linear Dynamic System：連續、線性) id8 --> id11(Particle Filter: 非高斯、非線性)

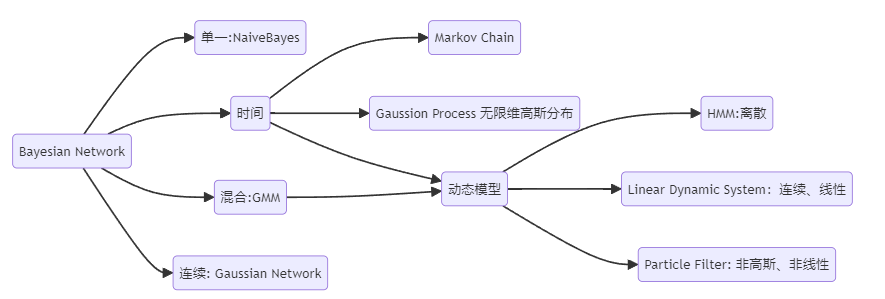
從單一到混合、從有限到無限：
空間：隨機變數的取值從離散到連續
時間：時間序列模型從有限到無限，從某一時刻延長到無限時間

• Naive Bayes
  貝葉斯網路最簡單的模型

  graph TD y --> x1 y --> x2 y --> x3

• GMM

  graph LR z --> x

  其中 \(z\) 是離散的，\(x|z \to \mathcal{N}\)

3. Markov Random Field（無向圖模型）

條件獨立性

條件獨立性體現在以下三個方面，且能互相推出：

無向圖的全域性馬爾可夫性：給定兩個隨機變數集合的分離集，兩個隨機變數集合之間條件獨立。

區域性馬爾可夫性：

graph TD a --- b a --- c a --- d d --- e

\(a \perp (全集 - a - \text{neighbour of a}) | \text{neighbour of a}\)

成對馬爾可夫性:

\(x_i \perp x_j | x_{-i-j}\) 其中\(x_i,x_j\)不能相鄰

因子分解

無向圖在因子分解時沒有明確的方向性，因此要有額外的考慮

需要引入概念：

1. 團：關於節點的集合，團中的節點形成一個完全圖（所有的節點之間都有邊）
2. 極大團：團中不能再加入其他節點形成團(return 極大團是一個 NP-hard 問題)

團分解：將聯合機率分解為多個團的勢函式乘積

所有團的集合記為\(C\), 與團\(c\)對應的變數集合\(x_c\),勢函式\(\psi_c(x_c) \geq 0\)

\[p(x_1, \dots, x_p) = \frac{1}{Z} \prod_{c \in C} \psi_c(x_c) \]

其中 Z 是歸一化因子，使得機率和為 1,\(Z = \sum_x \prod_{c \in C} \psi_c(x_c)\)

Mark: \(\psi_c(x_c)\)取值隨著 x_c 中的 x 取值改變而改變

接下來的問題時如何構建勢函式，使得因子分解與條件獨立性一致。

然而，當變數個數較多時，團的數量會很多，因此需要簡化，注意到團被極大團包含，因此可以使用極大團來簡化。\(C^*\)為極大團的集合。

\[p(x_1, \dots, x_p) = \frac{1}{Z} \prod_{c \in C^*} \psi_c(x_c) \]

Hammesley-Clifford 定理

如果聯合機率分佈能夠使用極大團勢函式表示，那麼由該定理可以證明，因子分解與條件獨立性的三個性質等價。

如何使用因子分解

為了滿足非負性，我們一般定義勢函式（Gibbs Distribution）

\[\psi_Q(x_Q) = \exp(-H_Q(x_Q)) \]

那麼此時，聯合機率分佈為

\[p(x_1, \dots, x_p) = \frac{1}{Z} \prod_{c \in C^*} \psi_c(x_c) = \frac{1}{Z} \prod_{c \in C^*} \exp(-H_c(x_c)) = \underbrace{\frac{1}{Z} \exp(-\sum_{c \in C^*} H_c(x_c))}_{\text{指數族分佈}} \]

經過一通亂七八糟的說明之後，我們可以得知，Markov Random Field 與 Gibbs Distribution 是等價的。

4. Inference

總體來講，Inference 是指求解已知資料的機率，而求已知資料的機率時需要模型的引數，但是如果將引數看作未知的變數，那麼學習的過程也可以被看作是 Inference 的過程。

Inference 主要分為兩類：

1. \(p(x_E)\)
2. \(p(x_F | x_E)\), 而 \(p(x_F | x_E)\)又可以被寫作
3. MAP: \(\arg \max_{x_F} p(x_F | x_E)\)

\[p(x_F | x_E) = \frac{p(x_F, x_E)}{p(x_E)} \]

實際上 Inference 過程最主要的問題就是求解邊緣分佈的過程。

• 精確推斷
  • 動態規劃/變數消除/Variable Elimination
  • 信念傳播/Belief Propagation
  • Junction Tree
• 近似推斷
  • 確定性近似：變分推斷
  • 隨機近似：MCMC

Variable Elimination

graph LR x1 --> x2 x2 --> x3 x3 --> x4 x3 --> x5

\(x_5\)的邊緣機率分佈求解為

\[P(x_5) = \sum_{x_1} \sum_{x_2} \sum_{x_3} \sum_{x_4} P(x_1, x_2, x_3, x_4, x_5) \]

在這個過程中，如果直接計算，複雜度將會是\(O(|x_1||x_2||x_3||x_4|)\)，但是在其中有很多冗餘的計算，因此可以使用動態規劃的思想，將已經計算過的值儲存起來，這樣可以將複雜度降低到\(O(|x_1| + |x_2| + |x_3| + |x_4|)\)。

\[= \sum_{x_1} \sum_{x_2} \sum_{x_3} \sum_{x_4} P(x_1) P(x_2 | x_1) P(x_3 | x_2) P(x_4 | x_3) P(x_5 | x_3) = \\ \sum_{x_3} P(x_5 | x_3) \sum_{x_4} P(x_4 | x_3) \sum_{x_2} P(x_3 | x_2) \sum_{x_1} P(x_2 | x_1) P(x_1) \]

可以定義中間函式：

\[m_{12}(x_2) = \sum_{x_1} P(x_2 | x_1) P(x_1) \\ m_{23}(x_3) = \sum_{x_2} P(x_3 | x_2) m_{12}(x_2) \dots \]