正在完善!
氣泡排序
氣泡排序是一種簡單的排序演算法。它重複地走訪過要排序的數列,一次比較兩個元素,如果它們的順序錯誤就把它們交換過來。走訪數列的工作是重複地進行直到沒有再需要交換,也就是說該數列已經排序完成。這個演算法的名字由來是因為越小的元素會經由交換慢慢“浮”到數列的頂端。
1.1 演算法描述
- 比較相鄰的元素。如果第一個比第二個大,就交換它們兩個;
- 對每一對相鄰元素作同樣的工作,從開始第一對到結尾的最後一對,這樣在最後的元素應該會是最大的數;
- 針對所有的元素重複以上的步驟,除了最後一個;
- 重複步驟1~3,直到排序完成。
1.2 動圖演示
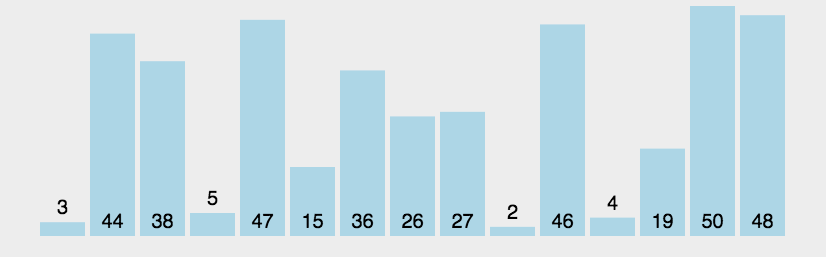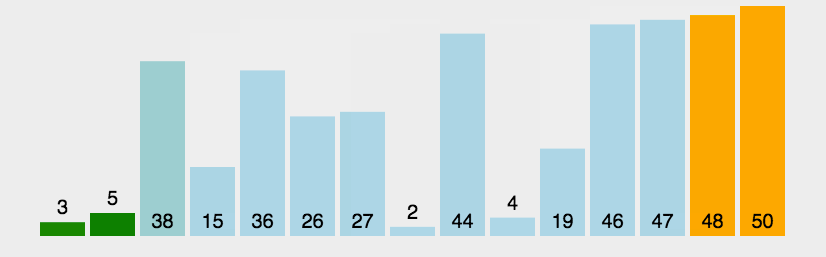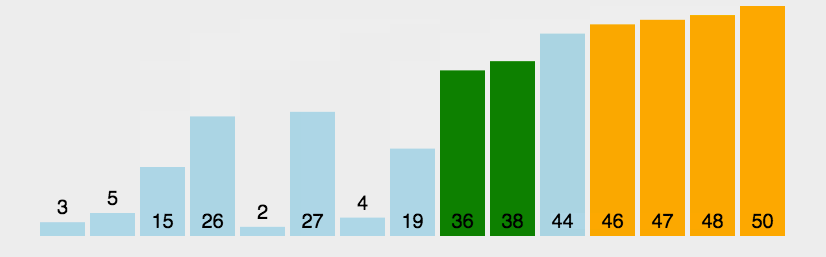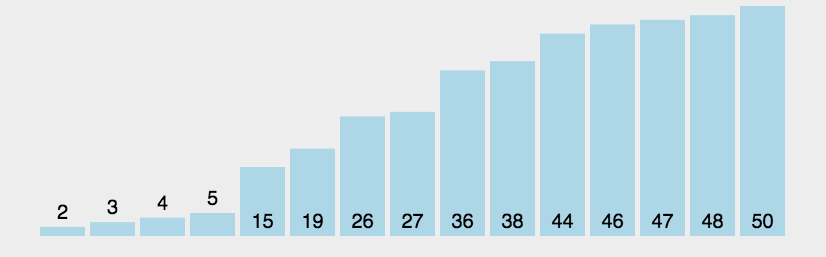
選擇排序
在長度為N的無序陣列中,第一次遍歷n-1個數,找到最小的數值與第一個元素交換;
第二次遍歷n-2個數,找到最小的數值與第二個元素交換;
。。。
第n-1次遍歷,找到最小的數值與第n-1個元素交換,排序完成。
插入排序
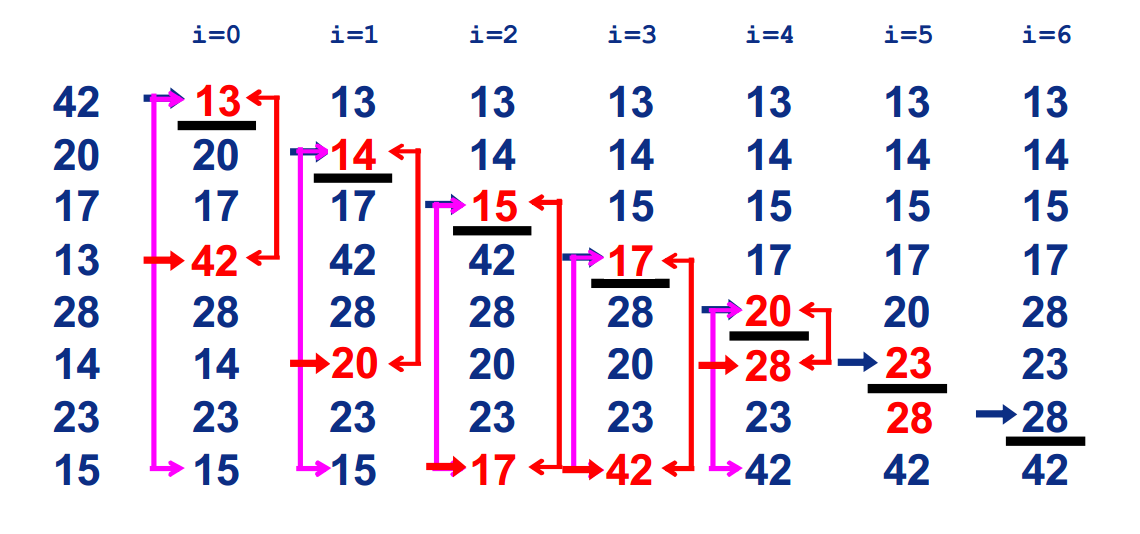
在要排序的一組數中,假定前n-1個數已經排好序,現在將第n個數插到前面的有序數列中,使得這n個數也是排好順序的。如此反覆迴圈,直到全部排好順序。

對於未排序資料(右手抓到的牌),在已排序序列(左手已經排好序的手牌)中從後向前掃描,找到相應位置並插入。
插入排序在實現上,通常採用in-place排序(即只需用到O(1)的額外空間的排序),因而在從後向前掃描過程中,需要反覆把已排序元素逐步向後挪位,為最新元素提供插入空間。
具體演算法描述如下:
- 從第一個元素開始,該元素可以認為已經被排序
- 取出下一個元素,在已經排序的元素序列中從後向前掃描
- 如果該元素(已排序)大於新元素,將該元素移到下一位置
- 重複步驟3,直到找到已排序的元素小於或者等於新元素的位置
- 將新元素插入到該位置後
- 重複步驟2~5
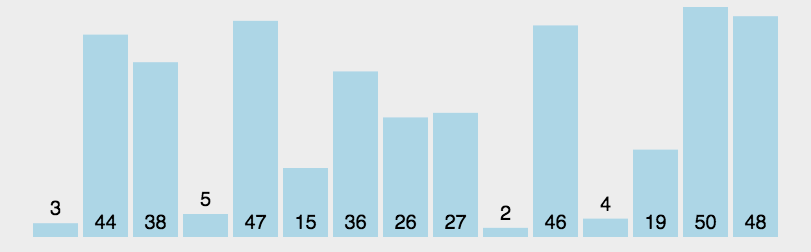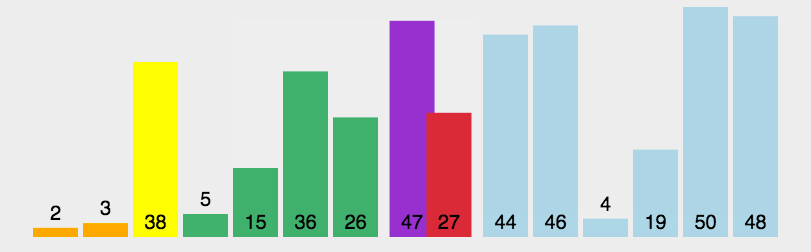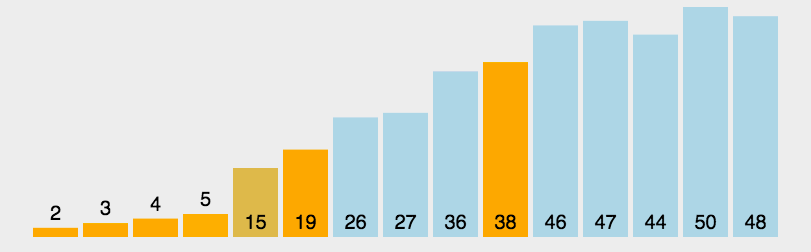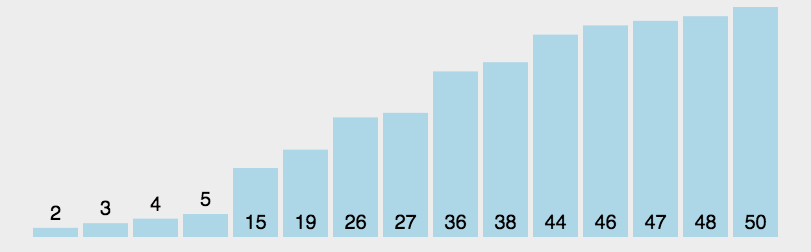
希爾排序
希爾排序是把記錄按下標的一定增量分組,對每組使用直接插入排序演算法排序;隨著增量逐漸減少,每組包含的關鍵詞越來越多,當增量減至1時,整個檔案恰被分成一組,演算法便終止。
原理是透過引入一個增量序列,採取分組排序策略,將大陣列分為若干個子序列,對每個子序列進行插入排序。隨著增量逐漸減小,子序列變得更小,最終達到增量為1,整個陣列變成一個有序序列,完成排序。
希爾排序(Shell Sort)是一種改進的插入排序演算法,由D.L.Shell於1959年提出。它的基本思想是將待排序的序列分割成若干個子序列,分別進行直接插入排序,待整個序列中的記錄基本有序時,再對全體記錄進行一次直接插入排序。這種排序方法透過引入間隔序列(增量),使得排序過程在開始階段就能夠更好地利用區域性有序性,從而提高效率。
希爾排序的主要動機是觀察到插入排序在處理小規模資料時的高效性。然而,對於大規模資料,插入排序需要進行大量的元素交換,尤其是在資料分佈不均時。希爾排序透過分組和調整步長,減少了排序過程中的比較和交換次數。它能夠利用插入排序對於部分有序資料的良好效能,同時透過分組和調整步長,減少了不必要的比較與交換。
希爾排序的預排序階段透過插入排序讓序列接近有序,這一過程稱為預排序。然後,隨著增量的逐漸減小,子序列變得更小,最終達到增量為1,整個陣列變成一個有序序列。這種排序方式使得希爾排序在初始階段,使用較大的步長讓序列更快時間的接近有序,並且減少了不必要的比較與交換。
簡單插入排序很循規蹈矩,不管陣列分佈是怎麼樣的,依然一步一步的對元素進行比較,移動,插入,比如[5,4,3,2,1,0]這種倒序序列,陣列末端的0要回到首位置很是費勁,比較和移動元素均需n-1次。而希爾排序在陣列中採用跳躍式分組的策略,透過某個增量將陣列元素劃分為若干組,然後分組進行插入排序,隨後逐步縮小增量,繼續按組進行插入排序操作,直至增量為1。希爾排序透過這種策略使得整個陣列在初始階段達到從宏觀上看基本有序,小的基本在前,大的基本在後。然後縮小增量,到增量為1時,其實多數情況下只需微調即可,不會涉及過多的資料移動。
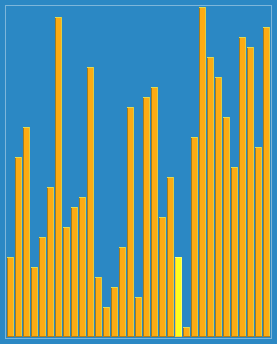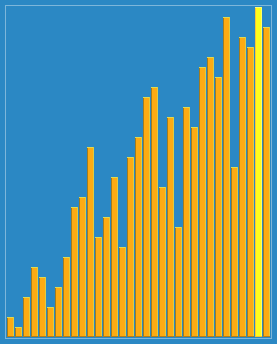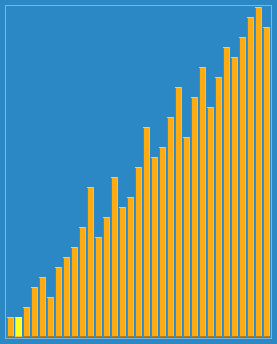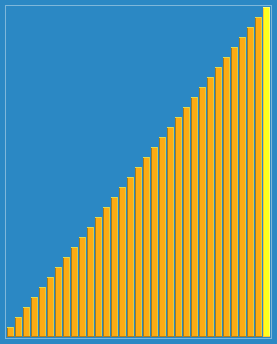
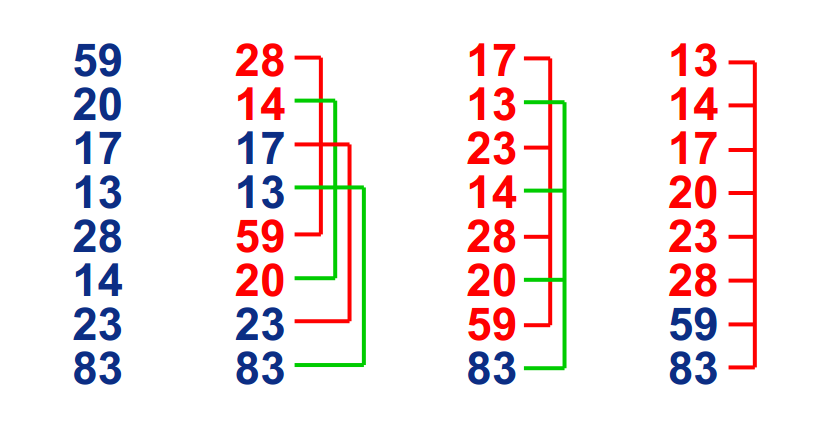
我們來看下希爾排序的基本步驟,在此我們選擇增量gap=length/2,縮小增量繼續以gap = gap/2的方式,這種增量選擇我們可以用一個序列來表示,{n/2,(n/2)/2...1},稱為增量序列。希爾排序的增量序列的選擇與證明是個數學難題,我們選擇的這個增量序列是比較常用的,也是希爾建議的增量,稱為希爾增量,但其實這個增量序列不是最優的。此處我們做示例使用希爾增量。
圖解如下:
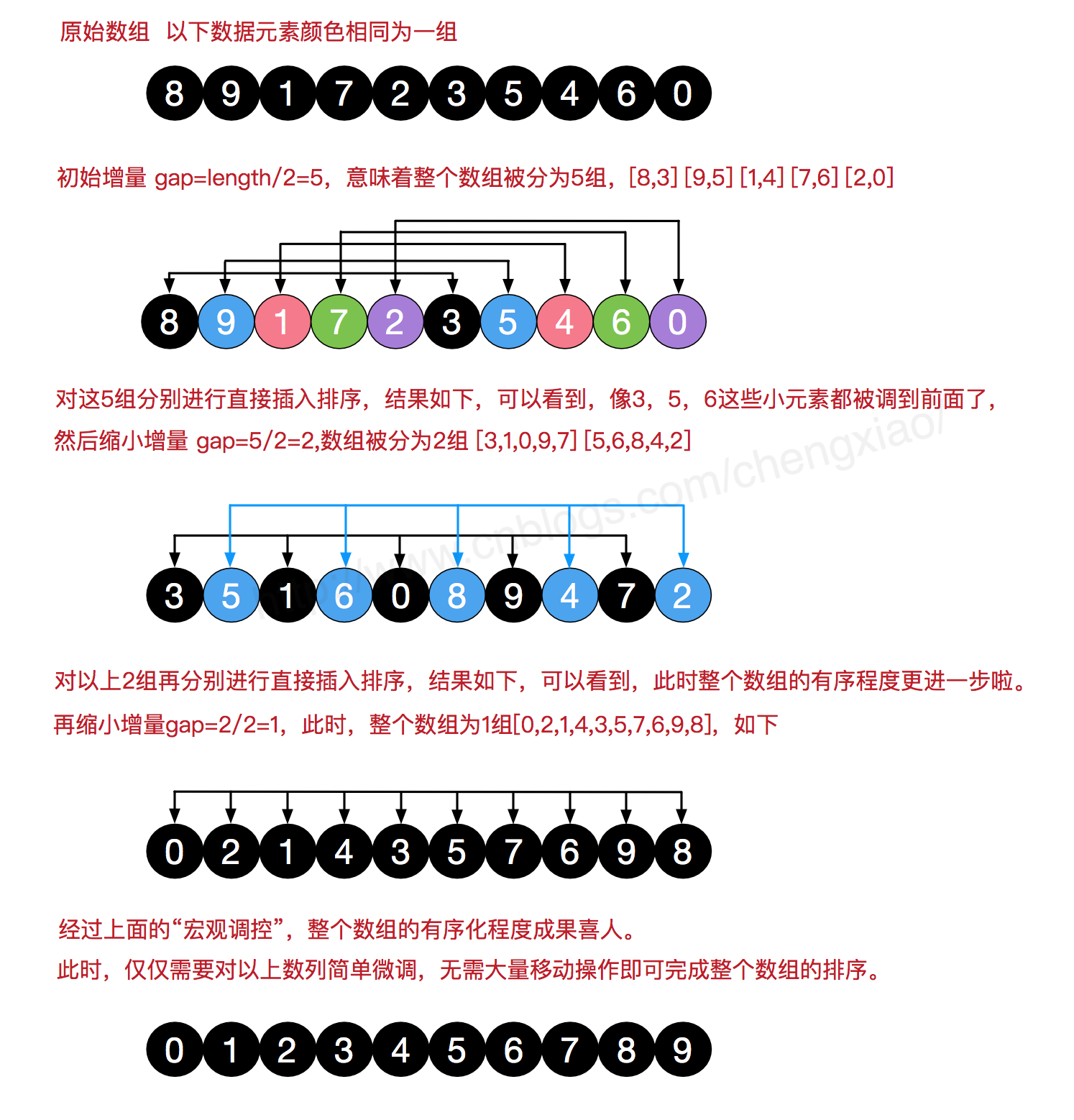
動圖如下:
堆排序
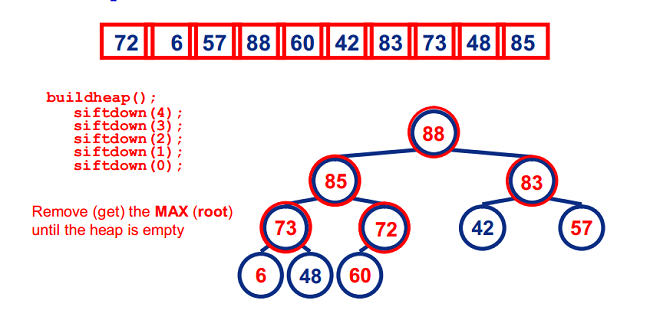
堆排序是指利用堆這種資料結構所設計的一種選擇排序演算法。堆是一種近似完全二叉樹的結構(通常堆是透過一維陣列來實現的),並滿足性質:以最大堆(也叫大根堆、大頂堆)為例,其中父結點的值總是大於它的孩子節點。
我們可以很容易的定義堆排序的過程:
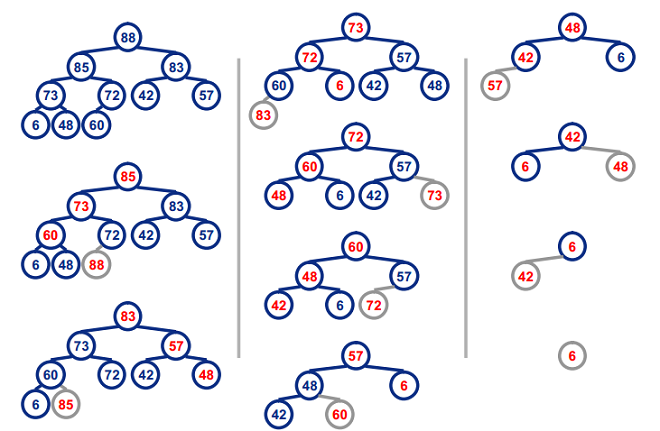
- 由輸入的無序陣列構造一個最大堆,作為初始的無序區
- 把堆頂元素(最大值)和堆尾元素互換
- 把堆(無序區)的尺寸縮小1,並呼叫heapify(A, 0)從新的堆頂元素開始進行堆調整
- 重複步驟2,直到堆的尺寸為1
歸併排序
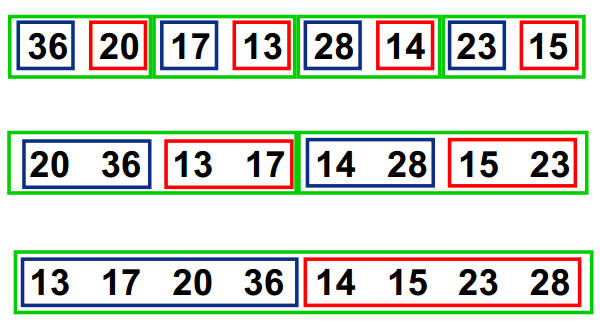
歸併排序是建立在歸併操作上的一種有效的排序演算法。該演算法是採用分治法的一個非常典型的應用。
首先考慮下如何將2個有序數列合併。這個非常簡單,只要從比較2個數列的第一個數,誰小就先取誰,取了後就在對應數列中刪除這個數。然後再進行比較,如果有數列為空,那直接將另一個數列的資料依次取出即可。
快速排序
快速排序是由東尼·霍爾所發展的一種排序演算法。在平均狀況下,排序n個元素要O(nlogn)次比較。在最壞狀況下則需要O(n^2)次比較,但這種狀況並不常見。事實上,快速排序通常明顯比其他O(nlogn)演算法更快,因為它的內部迴圈可以在大部分的架構上很有效率地被實現出來。
快速排序使用分治策略(Divide and Conquer)來把一個序列分為兩個子序列。步驟為:
- 從序列中挑出一個元素,作為"基準"(pivot).
- 把所有比基準值小的元素放在基準前面,所有比基準值大的元素放在基準的後面(相同的數可以到任一邊),這個稱為分割槽(partition)操作。
- 對每個分割槽遞迴地進行步驟1~2,遞迴的結束條件是序列的大小是0或1,這時整體已經被排好序了。