演算法導論
這個文件是學習“演算法設計與分析”課程時做的筆記,文件中包含的內容包括課堂上的一些比較重要的知識、例題以及課後作業的題解。主要的參考資料是 Introduction to algorithms-3rd(Thomas H.)(對應的中文版《演算法導論第三版》),除了這本書,還有的參考資料就是 Algorithms design techniques and analysis (M.H. Alsuwaiyel)。
隨機演算法
這裡將會討論另一種形式的演算法,放寬演算法對所有可能的輸入都必須得到正確解的要求,允許其可能會得到不正確的結果,這個可能的不正確效能夠因為其出現的機率極低而被安全忽略。並且也不再要求演算法每次執行某個特定的輸入都必須得到相同的結果,而是希望演算法在執行過程中能夠擲硬幣,產生真正隨機的結果。
引入隨機性並不會產生不可預測的結果,而是非常有用,並且能夠為非常低效的確定性演算法提供快速解決的方案。
在構建演算法的過程中,隨機化是一個非常重要的工具,因為隨機化的演算法能夠比確定性的演算法使用更少的時間和空間成本,並且隨機化的演算法通常也更加容易理解和實現。
隨機演算法可以被定義為除了輸入之外還接收隨即位元流的演算法,演算法可以在其操作過程中使用這個位元流來進行隨機選擇。
下面看一個例子,比如現在有一個 n 元多項式 \(f(x_1,x_2,...,x_n)\) ,並且希望確定這個多項式是否是恆等於0的。
如果要使用對 n 個變數逐個驗證的方法,那麼工作量將會是非常恐怖的。然而,如果使用隨機化的方法,隨機生成一個 n 維向量 \((v_1, v_2,...,v_n)\) 並帶入這個多項式,如果 \(f(v_1,...,v_n)\ne 0\),那麼這個多項式就不為0;否則,如果 \(f(v_1,...,v_n) = 0\) 那麼重複上面的步驟進行驗證,如果幾次驗證的結果都為0,那麼 f 大機率是恆等於 0 的多項式,也就是說這種情況下 f 不等於 0 的機率是可忽略的。
在一些確定演算法中,尤其是那些表現出良好的平均執行時間的演算法,只需要引入隨機化就能夠避免其糟糕的最壞情況,並使得該演算法能夠在每種可能的結果以高機率良好執行。
隨機演算法可以分為兩類:Las Vegas演算法和Monte Carlo演算法,下面將會分別討論這兩種演算法。
不過在正式開始之前有必要介紹衡量隨機演算法效能的標準。
對於一個確定的演算法 A ,衡量其效能的時間複雜度是指該演算法的平均執行時間,也就是對所有可能的輸入大小 n 的平均執行時間。這裡假設所有可能的輸入都是均勻分佈的,不過實際情況也有可能不是均勻分佈的。
對於一個隨機的演算法 A ,那麼對於一個大小為 n 的固定例項 I ,該演算法所使用的時間可能會發生變化。因此對於隨機演算法的效能評估標準是演算法 A 執行在固定例項 I 的執行時間的期望。也就是使用演算法 A 一次又一次的在例項 I 上執行的平均執行時間。
Las Vegas algorithm
Las Vegas演算法是指總是給出正確答案或者不給出答案的隨機演算法。
比如現在有一個陣列 A[1...n],其中 n 是偶數,這個陣列中有 (n/2) + 1 個元素取值都為 x ,而剩下的 (n/2) - 1 個元素的取值都與 x 不同,現在希望找到這個重複的元素 x,使用Las Vegas演算法的虛擬碼如下:

程式碼中的 "sample" 是指以均勻的機率隨機取樣,後面出現這個詞也是一樣的意思。
令 \(\Pr[success]\) 表示一次迭代中 \(i\ne j A[i] = A[j]\) 的機率,則:
\(\Pr[success] = \frac{n/2 + 1}{n}\times \frac{n/2}{n} \gt \frac{n/2}{n} \times \frac{n/2}{n} = \frac{1}{4}\)
因為第一次選擇重複的元素有 n/2 + 1 中可能,第二次選擇有 n/2 中可能。
那麼一次迭代中失敗的可能性就為 \(\Pr[failure] \le 3/4\)。那麼 k 次迭代都失敗的可能性為小於或者等於 \((3/4)^k\) 。因此,在 k 次迭代內成功的機率為\(1-(3/4)^k\)。
為了將這個機率寫成 \(1-(1/n)^c\) 的形式,令 \((3/4)^k = (1/n)^c\),則 \(k=c\log_{4/3}n\)。也就是說比如令c = 4,則該演算法能夠以 \(1-1/n^4\) 機率在 \(O(\log_{4/3} n)\) 的時間複雜度內得到正確的答案。
需要注意的是,在Las Vegas演算法中,機率與其執行時間相關,而結果總是正確的。
Monte Carlo algorithm
Monte Carlo演算法是指總是給出答案,但是有時會給出錯誤答案的演算法,但是給出錯誤答案的機率很低,可以忽略。
比如現在有一個陣列 A[1...n],其中 n 是偶數,現在希望能夠從該陣列中找到一個大於中位數的數,使用Monte Carlo演算法的虛擬碼如下:
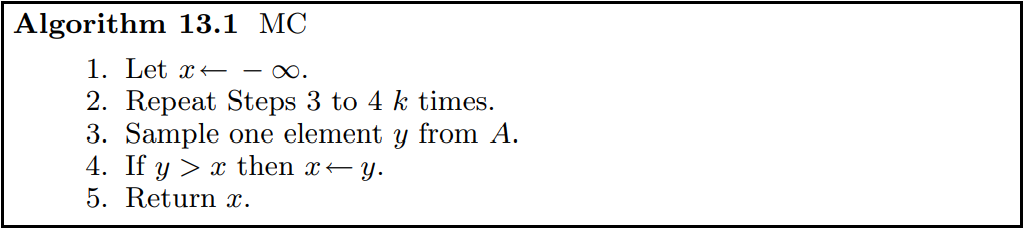
顯然,上述演算法迭代一次失敗的機率,即取樣的元素大於中位數的機率為 1/2,那麼 k 次迭代失敗的機率為 \(1/2^k\),所以 k 次迭代後取樣到一個大於中位數的機率為 \(1-1/2^k\)。
同樣,為了將這個機率寫成 \(1-1/n^c\) 的形式,令 \(1-1/2^k = 1-1/n^c\),則 \(k=c\log n\),也就是說比如令,c=4,則該演算法能夠在 \(O(\log n)\) 的時間複雜度內以 \(1-1/n^4\) 的機率得到正確解。
需要注意的是,在Monte Carlo演算法中,機率與正確性相關,而執行時間是固定的。
在另一個檔案中的演算法筆記中,介紹了隨機演算法在快速排序和選擇問題中的應用。