T1 逃離遺蹟
根據外星人的回信,在遺蹟中有分佈著三樣道具。當三樣道具都拿走後,遺蹟就很快自動毀滅,所以必須要在最短時間內離開。遺蹟可以看作是由N個房間(編號1..N)和N-1條長度不等通道所組成,並且任意兩個房間之間有且只有一條路可以相互到達。現在我們的隊員已經在編號為A,B,C的房間內拿到道具,並且準備撤退。由於只有一架直升機,所以只能在一個房間上停留。現在請你決定將直升機停在哪一個房間之上,能夠使三人到達該房間的距離之和最短。
考慮最短路模型,對 \(A, ~ B, ~ C\) 三個點分別作為源點跑一次最短路,掃一遍所有的點,找到 \(dist[A] + dist[B] + dist[C]\) 最小的點即可。
T2 遺址
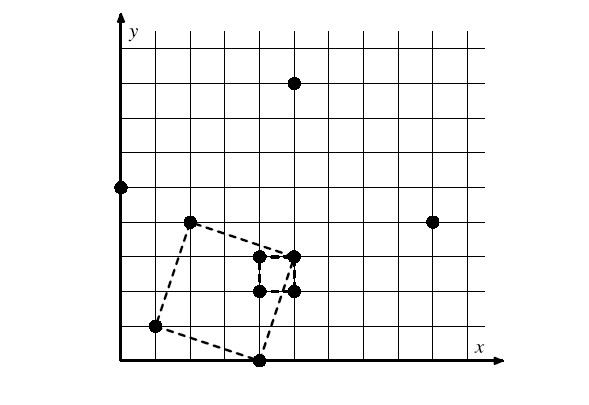
很久很久以前有一座寺廟,從上往下看寺廟的形狀正好是一個正方形,在4個角上豎立著圓柱搭建而成。現在圓柱都倒塌了,只在地上留下圓形的痕跡,可是現在地上有很多這樣的痕跡,專家說一定是最大的那個。
寫一個程式,給出圓柱的座標,找出由4個圓柱構成的最大的正方形,因為這就是寺廟的位置,要求計算出最大的面積。注意正方形的邊不一定平行於座標軸。
例如下圖有10根柱子,其中(4,2),(5,2),(5,3),(4,3)可以形成一個正方形,(1,1),(4,0),(5,3),(2,4)也可以,後者是其中最大的,面積為10。
考慮列舉正方形對角線上兩點 \((x_1, ~ y_1), ~ (x_2, ~ y_2)\),可以輕鬆計算出另外兩點的座標,判斷另外兩點是否存在即可,如果存在,則更新我們的答案,初始化答案為 \(-1\),如果結果為 \(-1\) 則不存在正方形。
T3 迷之階梯
在經過地球防衛小隊的數學家連續多日的工作之後,外星人發的密碼終於得以破解。它告訴我們在地球某一處的古老遺蹟中,存在有對抗這次災難的秘密道具。防衛小隊立刻派出了一個直升機小分隊,迅速感到了這處遺蹟。要進入遺蹟,需要透過一段迷之階梯。登上階梯必須要按照它要求方法,否則就無法登上階梯。它要求的方法有以下三個限制:
- 如果下一步階梯的高度只比當前階梯高1,則可以直接登上。
- 除了第一步階梯外,都可以從當前階梯退到前一步階梯。
- 當你連續退下k後,你可以一次跳上不超過當前階梯高度2^k的階梯。比如說你現在位於第j步階梯,並且是從第j + k步階梯退下來的。那麼你可以跳到高度不超過當前階梯高度 + 2^k的任何一步階梯。跳躍這一次只算一次移動。
開始時我們在第1步階梯。由於時間緊迫,我們需要用最少的移動次數登上迷之階梯。請你計算出最少的移動步數。
考慮動規,不妨設 \(dp[i]\) 表示到達第 \(i\) 級別階梯即 \(h[i]\) 高度時的最少步數,我們模擬每個後退的過程,記錄後退了 \(k\) 步,對於 \(i\) 以後的階梯 \(t\) 只要滿足 \(h[t] - h[i - k] <= (1 << k)\) 即可轉移 \(dp[t] = min(dp[t], dp[i - 1] + k + 1)\),我們可以列舉 \(t\) 和 \(k\) 完成轉移,這樣是 \(O(n^3)\) 的,不過足以透過此題了,此題還有 \(O(n^2)\) 的做法,歡迎同學對程式碼改進。
參考程式碼
#include<bits/stdc++.h>
using namespace std;
const int N = 210;
int n, h[N], dp[N];
int main()
{
cin >> n;
memset(dp, 0x3f, sizeof dp), dp[1] = 0;
for (int i = 1; i <= n; i ++ ) cin >> h[i];
for (int i = 2; i <= n; i ++ )
for (int j = i - 1, k = 0; j; j -- , k ++ )
for (int t = i; t <= n; t ++ )
if (k >= 31 || h[t] - h[j] <= (1 << k))
dp[t] = min(dp[t], dp[i - 1] + k + 1);
cout << (dp[n] == 0x3f3f3f3f ? -1 : dp[n]);
return 0;
}
T4 買票
週末Ztc想去劇場看演出,但他沒有票。這時,救世主Wzj出現了,他慷慨地願意賣給Ztc一些票。
Wzj手上共有n張票,但每張票的費用都不一樣,貪心的ztc想要得到儘可能多的票,但又想花費最少,慷慨的wzj願意給連續的m張票。
Ztc希望你能幫助他在花錢範圍內取得最大的票數。
雙指標板題,考慮擴大右指標後,左指標右移使得區間和小於上界,對區間和取 \(max\) 即可。