貪心演算法有時也很有用 - hashnode

貪心演算法
貪心演算法始終選擇最佳的可用選項。通常，它們在計算上比其他演算法系列（如動態程式設計或蠻力）便宜。那是因為他們沒有過多地探索解決方案空間。而且，出於同樣的原因，他們沒有找到解決許多問題的最佳解決方案。
但是，貪心策略可以解決許多問題，而該策略正是最好的解決方法。
Dijkstra演算法是最流行的貪心演算法之一，該演算法以最小的代價找到圖中從一個頂點到另一個頂點的路徑。該演算法透過始終轉到最近的頂點來找到這樣的路徑。這就是為什麼我們說這是一個貪心的演算法。
這是演算法的虛擬碼。我用G圖和s源節點表示。

Dijkstra(G, s):
    distances <- list of length equal to the number of nodes of the graph, initially it has all its elements equal to infinite

    distances[s] = 0

    queue = the set of vertices of G

    while queue is not empty:

          u <- vertex in queue with min distances[u]

          remove u from queue

          for each neighbor v of u:
              temp = distances[u] + value(u,v)

              if temp < distances[v]:
                   distances[v] = temp
     return distances

貪心的時候最糟糕
在上一節中，我們看到了使用貪心策略可以解決的兩個問題示例。這很棒，因為它們是非常快的演算法。
但是，正如我所說，Dijkstra的演算法不適用於帶有負邊的圖形。而且問題甚至更大。我總是可以用Dijkstra的解決方案達到我想要的效果來構建帶有負邊緣的圖形！考慮以下示例，該示例是從Stackoverflow提取的

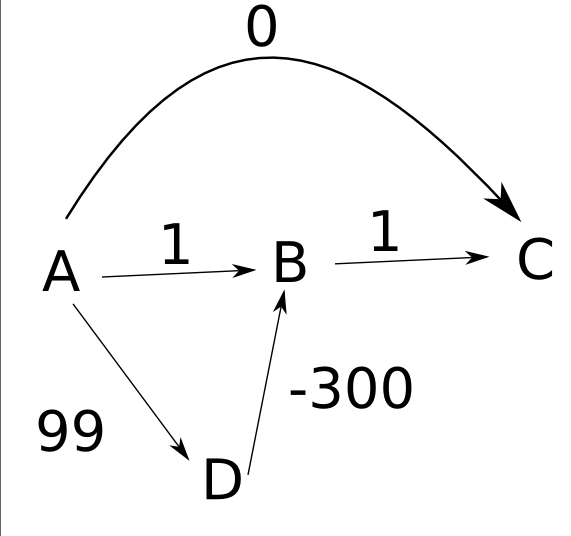
Dijkstra演算法未能找到之間的距離A和C。查詢d(A, C) = 0何時應為-200。並且，如果減小edge的值D -> B，我們將獲得一個距離實際最小距離甚至更遠的距離。
類似地，當我們無法在揹包問題（0-1揹包問題）中破壞物件時，使用貪心策略獲得的解決方案可能會像我們想要的那樣糟糕。我們總是可以為使貪婪演算法嚴重失敗的問題建立輸入。
 
另一個例子是旅行者問題（TSP）。給定一個城市列表以及每對城市之間的距離，最精確的路線是什麼？
我們可以總是去最近的城市來貪心地解決問題。我們選擇任何一個城市作為第一個城市並應用該策略。
正如前面的示例中所發生的那樣，我們總是可以透過貪心策略找到最糟糕的解決方案的方式來構建城市。
在本節中，我們看到了貪心的策略可能導致我們陷入災難。但是存在一些問題，其中這種方法可以很好地逼近最佳解決方案。
 

貪心的時候還不錯
我們已經看到，貪心策略對於某些問題來說是我們想要的那樣糟糕。這意味著我們不能用它來獲得最優解，甚至不能很好地近似它。
但是，在某些示例中，貪心演算法為我們提供了很好的近似值！在這些情況下，貪心方法非常有用，因為它往往更便宜且更易於實現。
圖的頂點覆蓋是最小的一組頂點，以使圖的每個邊緣在該集中具有至少一個端點。
這是一個非常困難的問題。實際上，沒有任何有效且精確的解決方案。但是，好訊息是我們可以使用貪心演算法進行近似。
我們<u, v>從圖中選擇任何邊，然後將u和新增v到集合中。然後，我們刪除所有具有u或v作為端點之一的邊，並在其餘圖具有邊的同時重複上一過程。
這可能是先前演算法的虛擬碼。

vertexCover(G):
    VertexCover <- {} // empty set
    E' <- edges of G

    while E' is not empty:
          VertexCover <- VertexCover U {u,v} where <u,v> is in E'
          E' = E' - {<u, v> U edges incident to u, v}

     return VertexCover