分而治之
分而治之(divide and conquer,D&C)是一種著名的遞迴式問題解決方法。
只能解決一種問題的演算法畢竟用處有限,而D&C提供瞭解決問題的思路,是另一個可供你使用的工具。
D&C演算法是遞迴的。使用D&C解決問題的過程包括兩個步驟。
(1) 找出基線條件,這種條件必須儘可能簡單。
(2) 不斷將問題分解(或者說縮小規模),直到符合基線條件。
例1
假設你是農場主,有一小塊土地。如何將一塊地均勻地分成方塊,並確保分出的方塊是最大的呢?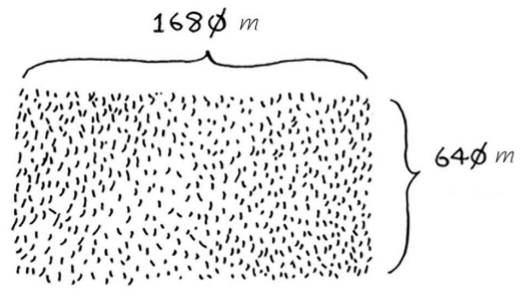
基線條件
最容易處理的情況是,一條邊的長度是另一條邊的整數倍。比如,25m x 50m的土地可以分成 2 個 25m x 25m 的方塊。
遞迴條件
根據D&C的定義,每次遞迴呼叫都必須縮小問題的規模。首先找出這塊地可容納的最大方塊。如,上圖可以劃出兩個640 m × 640 m的方塊,同時餘下一小塊400m x 640m 地。
我們下一步要做的就是對餘下的那一小塊地使用相同的演算法。因為適用於這小塊地的最大方塊,也是適用於整塊地的最大方塊。換言之,你將均勻劃分1680 m × 640 m土地的問題,簡化成了均勻劃分400m x 640 m土地的問題!
我們很容易實現上述過程。我們進一步抽象,這個過程實際上就是求兩個整數的最大公倍數。
例2
給定一個數字陣列,如,[2,4,6],怎麼返回這些數字相加後的結果。使用迴圈可以很容易實現。那使用遞迴怎麼實現呢?
基線條件
最簡單的陣列不包含任何元素或只包含一個元素,這個可以認為是陣列的基線條件。
遞迴條件
每次遞迴呼叫都必須離空陣列更近一步。我們透過下面的等式縮小問題的規模。sum [2,4,6] == 2 + sum [4,6]
使用Haskell可以很容易實現:
sum [] = 0
sum (x:xs) = x + (sum xs)快速排序
快速排序是一種常用的排序演算法,如,C語言標準庫中的函式qsort實現的就是快速排序。
基線條件
陣列為空或只包含一個元素。在這種情況下,只需原樣返回陣列。
遞迴條件
我們從陣列中選擇一個元素作為基準值(pivot),然後以該值為基準對資料分割槽(partitioning),這樣陣列劃分成了三部分:
- 一個由所有小於基準值的數字組成的子陣列;
- 基準值
- 一個由所有大於基準值的陣列組成的子陣列。
這樣問題縮小到了子陣列規模。再分別對子陣列應用以上過程,得到排序後的子陣列,最終我們只要將這三部分拼接起來就能得到完全排序的陣列。
注意:為了實現簡單,基準值每次都取的陣列首元素。
程式碼如下:
# python
def quicksort(array):
if len(array) < 2:
return array
else:
pivot = array[0]
less = [i for i in array[1:] if i <= pivot]
greater = [i for i in array[1:] if i > pivot]
return quicksort(less) + [pivot] + quicksort(greater)--haskell
import Data.List
quickSort :: Ord a => [a] -> [a]
quickSort [] = []
quickSort (x:xs) = quickSort lhs ++ [x] ++ quickSort rhs
where
(lhs, rhs) = partition (< x) xs注意:上面的版本每次都新生成子陣列,有些人認為正確的快速排序應該使用in-place交換,所以上面的演算法不“正宗”。
再談大 O 表示法
快速排序的獨特之處在於,其速度取決於選擇的基準值。在平均情況下,快速排序的執行時間為O(nlog n),在最糟情況下,退化為O(n2)。還有一種合併排序(merge sort)的排序演算法,其執行時間為O(nlogn)。
大O表示法體現出的是對元素規模n的增速,但處理每個元素的速度是有差異的,比如,對每個元素執行(*2)和(+3).(*2)操作,明顯是後者執行的時間長。
快速排序和合並排序的演算法速度分別表示為c1 nlogn和c2 nlogn,c是演算法所需的固定時間量,被稱為常量。通常不考慮這個常量,因為如果兩種演算法的大O執行時間不同,這種常量將無關緊要。但有時候,常量的影響可能很大,對快速查詢和合並查詢來說就是如此。快速查詢的常量比合並查詢小,因此如果它們的執行時間都為O(n log n),快速查詢的速度將更快。實際上,快速查詢的速度確實更快,因為相對於遇上最糟情況,它遇上平均情況的可能性要大得多。