組合數
定義:\(\begin{pmatrix}n\\m\end{pmatrix}\) 表示 \(n\) 元集的 \(m\) 元子集個數。
通項
考慮其組合意義:
把所有 \(n!\) 個排列的前 \(m\) 個元素作為選出集合,每個集合被計算 \(m!(n - m)!\) 次。
二項式定理
組合意義:從 \(n\) 個括號裡選出 \(i\) 個給 \(x\),剩下給 \(y\)。
因此第 \(n\) 行組合數的普通生成函式 \(F_n(x)\) 的封閉形式為:
組合數的對稱性
組合數的吸收公式
遞推公式
組合意義就是討論第 \(n\) 個元素是不是選出的第 \(m\) 個元素。
從生成函式的角度理解:\(F_n(x) = (x + 1) F_{n - 1}(x)\),對比係數得到遞推公式。
組合數的行和
組合數的列和
把和式中第一個非零項 \(\begin{pmatrix}m\\m\end{pmatrix}\) 看作 \(\begin{pmatrix}m + 1\\m + 1\end{pmatrix}\)。
- \(\binom{m + 1}{m + 1} + \binom{m + 1}{m} = \binom{m + 2}{m + 1}\)。
- \(\binom{m + 2}{m + 1} + \binom{m + 2}{m} = \binom{m + 3}{m + 1}\)。
以此類推得到 \(\begin{pmatrix}n\\m + 1\end{pmatrix} + \begin{pmatrix}n\\m\end{pmatrix} = \begin{pmatrix}n + 1\\m + 1\end{pmatrix} \)。
範德蒙德卷積
把 \(n + m\) 元集拆成一個 \(n\) 元集和一個 \(m\) 元集。
列舉 \(n + m\) 裡面選 \(k\) 個出來的所有方案與這個 \(n\) 元集的交集 \(i\),組合意義顯然。
一個很有用的公式
\(n\) 個裡面選 \(m\) 個,再在 \(m\) 個裡面選 \(r\) 個。
等價於 \(n\) 個裡面選 \(r\) 個,在剩下的 \(n - r\) 個裡再選 \(m - r\) 個。
容斥原理
考慮每個元素在右式被計算幾次。
如果一個元素在 \(k\) 個 \(S_i\) 中出現,那麼他會被計算 \(\sum_{i = 1}^k(-1)^{i - 1}\begin{pmatrix}k\\i\end{pmatrix} = [k\ne 0]\)。
因此左邊等於右邊。
很多情況下要求同時滿足 \(n\) 個條件的集合大小。
記 \(S_i\) 為不滿足第 \(i\) 個條件的集合,那麼答案即 \(\vert U\vert - \vert \bigcup_{i = 1}^n S_i\vert\)。
無限制的格路計數
題意:給定 \(n, m \ge 0\),你一開始在原點,每次可以從 \((x,y)\) 走到 \((x + 1, y + 1)\) 或 \((x + 1, y - 1)\),問走到 \((n, m)\) 的合法方案數。
設往右上走了 \(t\) 步,則往右下走了 \(n - t\) 步。
解方程 \(t - (n - t) = m\),\(t = \dfrac{n + m}{2}\)。
如果 \(2 \not\mid n + m\),那麼方案數為 \(0\),否則方案數為 \(\begin{pmatrix}n\\ \frac{n + m}{2}\end{pmatrix}\)。
從生成函式的角度理解,次數代表縱座標:
反射容斥
例1:給定 \(n, m \ge 0\) 以及 \(p < 0\),你一開始在原點,每次可以從 \((x,y)\) 走到 \((x + 1, y + 1)\) 或 \((x + 1, y - 1)\),
問不經過直線 \(y = p\) 上的點走到 \((n, m)\) 的合法方案數。
考慮用上個模型的方案數減去經過 \(y = p\) 的方案數。
對於一個經過 \(y = p\) 的方案,我們將 \(p\) 上方的路徑折下來,得到一條 \((0, 2p)\) 到 \((n, m)\) 的路徑,任意新路徑都能翻回去,因此這是一個雙射。
則合法方案數等於 \(\begin{pmatrix}n\\\frac{n + m}{2}\end{pmatrix} - \begin{pmatrix}n\\\frac{n + m - 2p}{2}\end{pmatrix}\)。
例2:給定 \(n, m \ge 0\) 以及 \(p < 0,\ q > m\),你一開始在原點,每次可以從 \((x,y)\) 走到 \((x + 1, y + 1)\) 或 \((x + 1, y - 1)\),
問不經過直線 \(y = p\) 和 \(y = q\) 上的點走到 \((n, m)\) 的合法方案數。
還是用總方案減去不合法的方案,問題轉化為經過 \(y = p\) 或 \(y = q\) 走到終點的方案數。
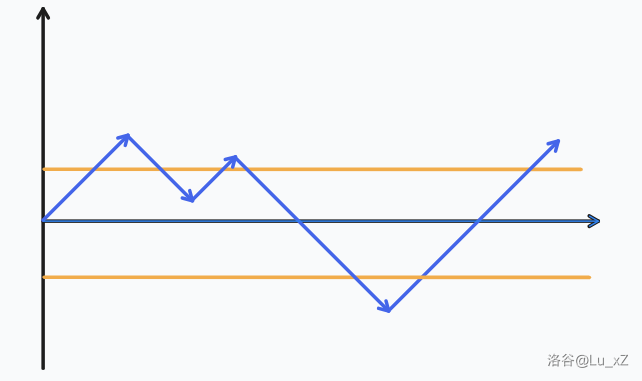
對於一條路徑,如果經過 \(y = p\) 就寫 'A',經過 \(y = q\) 就寫 'B',如圖路徑寫成 "BBBBAAB"。
把連續相同字元縮成一個,即 "BAB"。
每個路徑都可以對映成一個字串,字串 “AB” 表示一條先經過 \(y = p\) 再經過 \(y = q\) 的路徑,且沒有其他地方與限制相交。
欽定先經過 \(y = p\) 再經過 \(y = q\) 的方案如何求?先將起點延 \(y = p\) 翻折轉化為只有一條限制的情況,再延 \(y = q\) 翻折。
恰好呢?考慮上述計算方式會多計算哪些情況?
所謂 "AB",我們在計算過程中並不關心 "A" 前面有沒有 "B" 以及 "B" 後面有沒有 "A", "AB", "ABA"...。
也就是說,"BAB", "BABA"... 和 "ABA", "ABAB"... 都會在計算 "AB" 時被算到。
如何構造容斥係數使得每種非法情況("A", "B", "AB", "BA", "ABA"...)最後計算次數恰好為 \(-1\)。
從另一個角度考慮重複計算,如果 \(T\) 是 \(S\) 的子串,那麼 \(S\) 的所有路徑會在計算 \(T\) 時恰好被算一次。
對於字串 "ABABA",其本質不同子串有 "A", "AB", "ABA", "ABAB", "ABABA", "B", "BA", "BAB", "BABA"。共 \(2\vert S \vert - 1\) 個。
我們知道 \(\sum_{i = 1}^{2\vert S\vert -1}(-1)^{i} = -1\),因此把每種字串的容斥係數定為 \((-1)^{\vert S\vert}\) 可以恰好滿足條件。
由於每增加一個字元,橫座標就要增加至少 \(q - p\) 的長度,需要考慮的字串只有 \(O(\dfrac{n}{q - p})\)(不考慮從原點第一次到限制的距離,反正就是很少)。
卡特蘭數
定義:第 \(n \ge 0\) 項卡特蘭數 \(C_n\) 表示長度為 \(2n\) 的合法括號序列數。
通項
用反射容斥解釋這個式子。
左括號表示 \((x, y) \to (x + 1, y + 1)\),右括號表示 \((x, y) \to (x + 1, y - 1)\),卡特蘭數等於 \((0, 0)\) 走到 \((2n, 0)\) 不經過 \(y = -1\) 的路徑數。
這樣對映滿足了合法括號序列的充要條件:左括號 = 右括號;任意字首左括號不小於右括號。
遞推式
列舉第一個右括號之間有多少括號對:
透過遞推式解得卡特蘭數的生成函式
子集反演
只考慮第一個式子,第二個類似。
從左推右:
記 \(h(S) = \sum_{T \subseteq S} (-1)^{\vert S\vert - \vert T\vert}\)。
帶回原式:
從右推左:
二項式反演
引入
錯排問題:\(n\) 個人排列。第 \(i\) 個人不能在位置 \(i\),求合法排列數。
欽定 \(k\) 個人在自己位置上:
定義 \(f(n)\) 為 \(n\) 個人的排列數,\(g(n)\) 為 \(n\) 個人的錯排數。
問題在於 \(f\) 能夠快速計算,如何透過 \(f\) 反求 \(g\)。
有組合恆等式
說一句廢話:
把 \([n - m = 0]\) 用上面的恆等式帶掉:
公式
可以理解為 \(g(S)\) 只與 \(\vert S\vert\) 相關的子集反演。
實際應用中一般用第二種形式,\(f(n)\) 表示欽定 \(n\) 個的方案數,\(g(n)\) 表示恰好 \(n\) 個的方案數。
莫比烏斯反演
引入
週期問題:求長度為 \(n\) 的字串且週期(最小迴圈節)恰為 \(n\) 的字串個數,僅包含小寫字母。
定義 \(f(n)\) 為長度為 \(n\) 的字串個數,\(g(n)\) 為長度為 \(n\) 且週期恰為 \(n\) 的方案數。
顯然有 \(f(n) = 26^n\),怎麼反求 \(g\)?
設函式 \(\mu\) 滿足
構造一句廢話然後代入:
公式
從子集反演的角度理解這個公式。
把每個數 \(x\) 對映成一個無限長的向量,第 \(i\) 為表示正整數中第 \(i\) 個質數在 \(x\) 中的次數。
整除關係即集合之間的包含關係。
現在目的是從 \(f(n)\) 裡面減掉沒有頂滿(因子)的方案數。
只容斥與原數高度相差 \(1\) 的因子,減掉所有的 \(f(\dfrac{n}{p_i})\),加上所有 \(f(\dfrac{n}{p_ip_j})\),以此類推。
這同時也與 \(\mu\) 函式對應:存在平方因子(差兩格)則為 \(0\);否則為 \(-1\) 的質因子個數次方。
第二類斯特林數
\(\begin{Bmatrix}n\\m\end{Bmatrix}\) 表示把 \(n\) 元集劃分為 \(m\) 個互不區分的非空集合的方案數。
通項公式
先假定 \(m\) 個集合互相區分,最後除以 \(m!\)。
欽定部分集合為空,然後容斥。
遞推式
考慮最後一個元素 \(n\) 扔到哪裡。
選一個現有集合扔進去(雖然集合互不區分,但是元素互不相同);新增一個集合。
普通冪轉下降冪
\(x^n\) 表示 \(n\) 個元素分配給互相區分的 \(x\) 個集合的方案數。
選出 \(i\) 個集合,\(n\) 個元素分出 \(i\) 個非空集合的方案是 \(s(n, i)\),由於集合不區分,再乘一個 \(i!\)。
單位根反演
單位根:\(x^n = 1\) 在複平面上的 \(n\) 個解,其中 \(w_{n}^k = e^{i\frac{2k\pi}{n}}\)。
當 \(n \mid k\) 時,\(w_{n}^{ik} = 1\),右式等於 \(1\)。
否則右邊是一個等比數列,等於 \(\dfrac{1}{n}\times \dfrac{1 - w_{n}^{nk}}{1 - w_{n}^k} = 0\)。
用於模意義下的原根也是對的。
min-max 容斥
以第一種形式為例,第 \(k\) 小的元素被計算的次數等於:
實際應用一般結合期望,也就是如果一個集合的期望最小不好求,可以去求他的期望最大。
高維字首和
二維字首和:
for(int i = 1; i <= n; ++ i) {
for(int j = 1; j <= n; ++ j) {
a[i][j] += a[i - 1][j];
}
}
for(int i = 1; i <= n; ++ i) {
for(int j = 1; j <= n; ++ j) {
a[i][j] += a[i][j - 1];
}
}
三維字首和:
for(int i = 1; i <= n; ++ i) {
for(int j = 1; j <= n; ++ j) {
for(int k = 1; k <= n; ++ k) {
a[i][j][k] += a[i - 1][j][k];
}
}
}
for(int i = 1; i <= n; ++ i) {
for(int j = 1; j <= n; ++ j) {
for(int k = 1; k <= n; ++ k) {
a[i][j][k] += a[i][j - 1][k];
}
}
}
for(int i = 1; i <= n; ++ i) {
for(int j = 1; j <= n; ++ j) {
for(int k = 1; k <= n; ++ k) {
a[i][j][k] += a[i][j][k - 1];
}
}
}
子集和:
用偏序的形式表示子集和,可以發現他就是一個 \(n\) 維,每個維度只有 01 的字首和。
for(int i = 0; i < n; ++ i) { // 列舉維度,1011 用陣列表示為 a[1][1][0][1]
for(int s = 0; s < 1 << n; ++ s) {
if(s >> i & 1) a[s] += a[s ^ 1 << i];
}
}
子集和還有分治做法。
對於一個 \([0, 2^n)\) 的序列,每次把他分成兩部分 \([0, 2^{n - 1})[2^{n - 1}, 2^n)\)。
遞迴處理每個數在各自分治區間的子集和。
考慮合併兩部分資訊。
右邊部分的第 \(n - 1\) 位都是 \(1\),左邊部分的第 \(n - 1\) 位都是 \(0\),對應位呈現包含關係(\(x\) 對應 \(x + 2^{n - 1}\))。
因此右邊再加上左半邊對應的貢獻就可求得當前分治區間的子集和。
時間複雜度 \(T(2^n) = 2T(2^{n - 1}) + O(2^n) = O(n2^n)\)。
快速莫比烏斯變換
集合冪級數 \(F(x)\) 的莫比烏斯變換 \(\hat{F}(x)\) 滿足:
莫比烏斯變換即高維字首和。
莫比烏斯逆變換即高維差分,都可以按維 dp 做到 \(O(\vert U\vert2^{\vert U\vert})\)。
集合並卷積(或卷積)
求集合冪級數 \(H(x) = F(x)G(x)\),滿足
先求出 \(\hat{H}(x)\),再做逆變換。
推廣:集合交卷積(與卷積)
同樣令 \(\hat H(x)\) 表示 \(H\) 的變換:
類似的,只不過是高維字首和換成高維字尾和。
集合無交併卷積(子集卷積)
考慮在集合冪級數中引入未定元 \(y\),指數代表集合大小。
對 \(x\) 做集合並卷積,\(y\) 做乘法卷積,求得 \(H^\prime(x, y) = F^\prime(x, y) G^\prime(x, y)\),其中 \([x^Sy^{\vert S\vert}]F^\prime(x, y) = [x^S]F(x)\)。
兩個集合無交當且僅當 \(\vert S\cup T\vert = \vert S\vert + \vert T\vert\)。
因此有 \([x^S]H(x) = [x^Sy^{\vert S\vert}]H^\prime(x, y)\)。
我們把形式冪集數 \(F^\prime(x, y)\) 看作一個 \(\vert U\vert\) 行 \(2^{\vert U\vert}\) 的二維矩陣。
每一行保留大小為 \(i\) 的集合係數,其餘全為 \(0\)。
\(\vert U\vert^2\) 列舉 \(F^\prime\) 和 \(G^\prime\) 的行,然後做兩行的集合並卷積,時間複雜度 \(\vert U\vert^32^{\vert U\vert}\)。
考慮 \(\vert U\vert^22^{\vert U\vert}\) 預處理出每一行的莫比烏斯變換,暴力算 \(y\) 卷積時只要 \(O(\vert U\vert)\) 對應係數相乘。
莫比烏斯變換是線性變換,不需要每做一次卷積就要逆變換,係數可以累加。
最後對每一行做莫比烏斯逆變換,時間複雜度 \(O(\vert U\vert^22^{\vert U\vert})\)。
快速沃爾什變換
- 注意 \(T\) 的範圍是所有集合。
考慮分治。
對於 \([0, 2^n)\) 的區間,劃分為 \([0, 2^{n - 1})[2^{n - 1}, 2^n)\) 兩個子問題。
設 \(x\) 原來的係數為 \(f(x)\),考慮跨塊貢獻後的新系數為 \(f^\prime(x)\)。
對於一個右側元素 \(x + 2^{n + 1}\),左側對他的貢獻怎麼算?
發現左側對 \(x + 2^{n + 1}\) 的貢獻和原來對 \(x\) 的貢獻(即 \(f(x)\))是一樣的,因為左邊第 \(n - 1\) 位都為 \(0\)。
右側元素對 \(x + 2^{n + 1}\) 是否還是 \(f(x + 2^{n + 1})\)?
在 \([2^{n - 1}, 2^n)\) 裡做 FWT 時沒有考慮第 \(n - 1\) 位的貢獻,因此 \(f^{\prime}(x + 2^{n - 1}) = f(x) - f(x + 2^{n - 1})\)。
類似地考慮左半邊,\(f^{\prime}(x) = f(x) + f(x + 2^{n - 1})\)。
沃爾什逆變換
試著對 \(\hat F(x)\) 再做一遍沃爾什變換。
第二步中 \(\oplus\) 表示對稱差。\(S\) 和 \(R\) 的公共元素會對 \(-1\) 產生偶數次貢獻。
我們發現只要將 \(\hat{\hat F}(x)\) 的各項係數乘上 \(\dfrac{1}{2^{\vert U\vert}}\) 即可還原 \(F(x)\),即沃爾什逆變換。
集合對稱差卷積(異或卷積)
設 \(H(x) = F(x)G(x)\)。
burnside 引理
對於一個群 \((G, \times)\),裡面的元素都是作用於集合 \(X\) 的置換。
\(h = f \times g\implies \forall x \in X,\ h(x) = g(f(x))\)。
\((G, \times)\) 是群需要滿足:
- \(\forall a, b \in G,\ a \times b \in G\)。
- \(\forall a, b, c \in G,\ (a\times b) \times c = a\times (b \times c)\)。
- \(\exists e \in G,\ \forall a \in G,\ e \times a = a \times e = a\)。
- \(\forall a \in G,\exists b \in G,\ a \times b = e\),把 \(b\) 稱作 \(a\) 的逆元。
如果 \(X\) 中兩個元素可以透過 \(G\) 中置換變得相等,那麼稱他們等價,同屬一個等價類。
\(X\) 中的等價類個數等於
拉格朗日插值
假設已知多項式 \(f(x)\) 的 \(n\) 處點值 \((x_i, y_i)\),可以構造出滿足這些點值限制的多項式:
如果 \(f(x)\) 次數小於 \(n\),根據代數基本定理可知 \(f(x) = g(x)\)(我不會證)。
這意味著我們只需 \(n\) 個點值就能確定 \(f(x)\)。
點值表示做乘法時只有 \(O(n)\) 而非卷積的 \(O(n^2)\)。
透過點值還原 \(f(x)\) 可以先 \(O(n^2)\) 求出 \(\prod {x - x_j}\),然後對於求和的每一項 \(O(n)\) 除一個一次多項式即可。
CF722E Research Rover
題意:\(n \times m\) 的網格,圖上 \(k\) 個關鍵點。給定初始權值 \(s\),每經過一個關鍵點權值減半(上取整)。
每次只能向右或向下走,求從 \((1, 1)\) 走到 \((n, m)\) 的期望權值。
將關鍵點排序。
最終權值只與經過的關鍵點數有關, \(f_{i, j}\) 表示走到第 \(i\) 個關鍵點恰好選了 \(j\) 個的方案數。
不怎麼好轉移,定義 \(g_{i, j}\) 表示走到 \(i\) 個關鍵點至少走了 \(j\) 個的方案數。
由於我們將方案根據恰好經過的第 \(j - 1\) 個關鍵點進行分類,因此求得的 \(g\) 是不重不漏的。
當 \(j > 20\) 時權值一定削減為 \(1\),因此只需算到 \(j = 20\),剩下的貢獻用總方案減掉即可。
submission
CF1097G Vladislav and a Great Legend
題意:給定一顆 \(n\) 個節點的樹 \(T\),對應任意非空頂點集 \(X\),\(f(X)\) 定義為它在原圖的極小連通子圖中的邊數,求:
其中 \(n \le 10^5,\ k \le 200\),極小連通子圖可認為是保留所有邊的虛樹。
\(\begin{pmatrix}f(X)\\i\end{pmatrix}\) 的組合意義是從 \(X\) 的虛樹中選 \(i\) 條邊的方案數。
列舉虛樹根 \(x\) 統計貢獻。現在加入一顆子樹 \(v\)。
肯定是 \(v\) 裡的點集與已經訪問過子樹中的點集(紅色)進行配對,考慮一對點集產生多少方案。
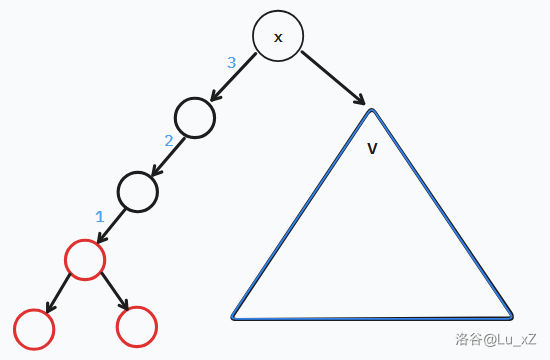
我們需要考慮 \(1\) 選不選,\(2\) 選不選,\(3\) 選不選。
雖然他們都不是紅色子樹中的邊,但是與 \(v\) 中點集配對後都會被經過。
設 \(f_{x, i}\) 表示以 \(x\) 為根的子樹內選中 \(i\) 條邊的生成樹個數(方案不一定合法)。
注意這裡選中的邊不一定是生成樹內部邊,也有可能是生成樹的根到 \(x\) 之間的邊。
現在考慮 \(v\) 子樹中的一棵生成樹。
生成樹內部以及生成樹的根到 \(v\) 之間的邊都已經決策過了,只要決策 \((x, v)\) 選還是不選。
其中 \(f^\prime\) 表示加入 \(v\) 後的 \(f\) 值。
注意這一部分的答案是要計入最終貢獻的,因為統計的都是合法方案。
假設 \(v\) 與右邊結合的方案已經計算完了。
現在要把一些只在 \(v\) 子樹的點集加入 \(f\),為下一棵子樹的轉移做準備。
點集的根到 \(v\) 都決策過了,還是考慮選不選 \((x, y)\)。
複雜度據說轉移時對 \(k\) 和子樹大小取 \(\min\) 就能做到 \(O(nk)\),很神秘。submission
CF1750G Doping
題意:疑似有點太難了。
CF1967E1 Again Counting Arrays (Easy Version)
題意:給定 \(n, m, b_0\),求長度為 \(n\) 的序列 \(a\) 個數,\(1 \le a_i \le m\) 且存在一個非負序列 \(b\) 滿足 \(\forall i \in [1, n], a_i \ne b_i\land\vert b_i - b_{i - 1} \vert = 1\)。
\(n, m, b_0 \le 2\times 10^5\)。
由於要保證 \(b_i\) 非負,貪心的使 \(b_i\) 儘可能大:
- \(b_{i - 1} + 1 \ne a_i \to b_i = b_{i - 1} + 1\)。
- \(b_{i - 1} + 1 = a_i \to b_i = b_{i - 1} - 1\)。
如果其中出現 \(b_i\) 為負,則序列 \(a\) 並不存在一個合法的 \(b\)。
顯然每個 \(a\) 可以按照這種方式唯一生成一個 \(b\),考慮對 \(b\) 計數。
\(f_{i, j}\) 表示滿足 \(b_i = j\) 的序列 \(a\) 個數。
第一種轉移 \((m - 1)f_{i, j} \to f_{i + 1, j + 1}\)。第二種轉移 \([j < m]f_{i, j} \to f_{i + 1, j - 1}\)。
如果第 \(i\) 個數已經到 \(m\) 了,後面隨便怎麼填都合法,不妨就用 \(f_{i, m}\) 記錄 \(j \ge m\) 的所有情況:\(mf_{i, m} \to f_{i + 1, m}\)。
時間複雜度 \(O(nm)\),不能透過。
從另一個角度考慮這個問題,把 \(b\) 的生成看作一個點從 \((0, b_0)\) 開始的遊走,碰到 \(y = m\) 或 \(x = n\) 則結束遊走。
如果第 \(i\) 步往右上走,說明 \(a_i\) 有 \(m - 1\) 種取值;否則 \(a_i\) 只有一種取值。
列舉 \(O(n)\) 種終點 \((i, m)\) 或 \((n, j)\),求從 \((0, b_0)\) 不經過 \(y = -1\) 和 \(y = m\) 到達終點的路徑數。
終點確定向右上和右下的步數也確定,往右上走對應 \(m - 1\) 種 \(a\) 的取值,往右下走對應唯一一種取值。
由於最後一步是確定的,反射容斥的終點設為 \((i - 1, m - 1)\) 可以規避一些邊界。反射容斥做到單次 \(O(\dfrac{n}{m})\)。
取閾值 \(B = \sqrt n\),按照 \(m\) 的大小分兩種做法,時間複雜度 \(O(nB + \dfrac{n^2}{B})\)。submission
P4221 [WC2018] 州區劃分
題意:\(n\) 個城市劃分為若干州。一個州合法當且僅當其生成子圖不存在尤拉回路。求所有合法劃分的滿意度之和。
一個劃分的滿意度等於所有州的滿意度之積。
第 \(i\) 個州的滿意度定義為第 \(i\) 個州的人口在前 \(i\) 個州的人口中所佔比例的 \(p\) 次冪,即
給出每個城市的人口 \(w_i\) 以及常數 \(p\),保證 \(n \le 21\) 且無重邊無自環。
\(O(m2^n)\) 預處理每個州 \(S\) 是否合法,\(S\) 中存在尤拉回路當且僅當子圖連通且所有點度數為偶。
記 \(W(S) = (\sum_{x \in S} w_x)^p\),\(f(S)\) 表示全集為 \(S\) 時的答案。
列舉 \(S\) 中最後一個州 \(T\):
把 \(W(S)\) 提出來,記 \(g(T) = \text{legal}(T) \times {W(T)}\),中間的 \(f(S\setminus T) \times g(T)\) 實際就是一個子集卷積(集合無交併)。
令 \([x^Sy^{\vert S\vert}]g^{\prime}(x, y) = [x^S]g(x)\),\(x\) 做或卷積,\(y\) 做乘法卷積。
把冪級數看作 \(n \times 2^n\) 的矩陣,每次列舉 \(f^{\prime}\) 的行 \(i\),和 \(g\) 的每行(除第 \(0\) 行)做或卷積,把答案累計到 \(j > i\) 的 \(f^{\prime}\) 上(乘法卷積使 \(y\) 的指數變大)。
時間複雜度 \(O(n^22^n)\)。submission
NFLSOJ 3392. 計算
題意:定義 \(F(x, a, b) = \gcd(x^a - 1, x^b - 1) + 1\),如果 \(a, b\) 其一為零則值為零。
給出 \(m, a, b, c, d\),令 \(L = F(m, a, b) + 1, R = F(m, c, d)\),保證 \(L < R \le 10^{18}, m \le 10^7\)。
求集合 \(\{L, L + 1, \cdots, R - 1, R\}\) 有多少個子集和能被 \(m\) 整除。
觀察 \(F\) 的定義,把他放在 \(x\) 進位制下考慮,不難發現 \(F(x, a, b) = x^{\gcd(a, b)}\),舉個十進位制的例子:\(\gcd(9999, 99) = \gcd(9999 - 9900, 99) = 10^{\gcd(4, 2)} - 1\)。
由於 \(L \equiv 1 \pmod m\) 且 \(R \equiv 0\pmod m\),因此每種餘數出現的次數都是 \(n = \dfrac{R - L + 1}{m}\)。
列舉子集和:
考慮如果 \(w_m^{ti} = w_m^{tj}\) 也就是 \(ti \equiv tj \pmod m\)。
那麼有 \(m \mid t(i - j)\),因此指數迴圈的最小正週期為 \(m/d\),且 \(0, d, 2d, \cdots, (m/d - 1)d\) 每個恰好出現一次,\(d = \gcd(t, m)\)。
(最小正週期內兩兩不同餘是顯然的,\(tj \equiv x \pmod m\) 的必要條件是 \(d \mid x\))
因此:
說明這個乘積與 \(t\) 無關,不妨直接列舉 \(d\):
根據分圓多項式 \(x^m - 1 = \prod_{i = 0}^{m - 1} (x - w_{m}^i)\):
暴力列舉因子,時間複雜度 \(O(\sqrt m + d(m)\log n)\)。submission
NFLSOJ 5005. 禮物
題意:計算有多少個不同的有 \(n\) 個珠子的手環,滿足有 \(m\) 個珠子是金色的,且金色珠子的最長連續段長度不超過 \(k\)。
兩個手環相同當且僅當它們可以透過旋轉變得一模一樣。\(1 \le n \le 10^6 , 0 \le k \le m \le n\)。
一共 \(n\) 種旋轉置換,第 \(i\) 個表示順時針轉 \(i\) 格,計算每種置換對應的不動點個數,最後除以 \(n\)。
考慮一種染色方案的最小正週期 \(T \mid n\),不妨破環成無限長的鏈,\(f(p) = f(p + T)\)。
如果存在 \(i\) 使得 \(f(p) = f(p + i)\),一定有 \(T \mid i\),即所有 \(T \mid \gcd(i, n)\) 的方案會被 \(i\) 計算到。
考慮列舉 \(d = \gcd(i, n)\) 作為週期,使每種最小正週期 \(T\mid d\) 被恰好算一次,有 \(\varphi(\frac{n}{d})\) 種置換滿足 \(d = \gcd(i, n)\)。
假設已經特判掉 \(d = n\) 的情況,現在可以把環拆成 \(\frac{n}{d}\) 個完全相同的部分(已經變成鏈了),對這部分計數。
\(n \gets d, m \gets \frac{md}{n}\)。不妨把 \(n - m\) 個白子先排列好,然後插空,滿足任意間隔不插超過 \(k\) 個。
最右邊的間隔不能填,因為和下一迴圈節的最左間隔等閒。那麼問題轉化為求不定方程 \(\sum_{i = 1}^{n - m} x_i = m,\ 0 \le x \le k\) 的解的數量。
欽定 \(z\) 個超過 \(k\),總和可以減掉 \((k + 1)z\),等價於 \(\sum_{i = 1}^{n - m} x_i = m - kz\) 的非負整數解數 \(\begin{pmatrix}n - (k + 1)z - 1\\ n - m - 1\end{pmatrix}\),因此可以 \(O(d)\) 容斥。
時間複雜度 \(\sum_{d \mid n} d = \sigma(n)\),即 \(O(n\log\log n)\)。submission