大俠幸會,在下全網同名[演算法金] 0 基礎轉 AI 上岸,多個演算法賽 Top [日更萬日,讓更多人享受智慧樂趣]
構建機器學習模型的關鍵步驟是檢查其效能,這是透過使用驗證指標來完成的。 選擇正確的驗證指標就像選擇一副水晶球:它使我們能夠以清晰的視野看到模型的效能。 在本指南中,我們將探討分類和迴歸的基本指標和有效評估模型的知識。 學習何時使用每個指標、優點和缺點以及如何在 Python 中實現它們。

1 分類指標
1.1 分類結果 在深入研究分類指標之前,我們必須瞭解以下概念:
- 真正例 (TP):模型正確預測正類的情況。
- 假正例 (FP):模型預測為正類,但實際類為負類的情況。
- 真反例 (TN):模型正確預測負類的情況。
- 假反例 (FN):模型預測為陰性類別,但實際類別為陽性的情況。
簡單來說,真正例和真反例,就像是模型正確識別出了正類與反類,而假正例和假反例。
1.2 準確度 準確率是最直接的分類指標,衡量正確預測的比例。雖然準確率易於理解和計算,但在類別不平衡的情況下,可能會產生誤導。在這種情況下,考慮其他指標是至關重要的。準確率的公式為:
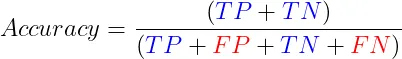
概括:
- 易於理解和溝通,並提供對模型效能的簡單評估。
- 不適合不平衡的類別,因為它可能有利於多數類別。
- 無法區分假陽性和假陰性。
- 應與其他指標結合使用。
這是一種在 Python 中計算準確度得分的方法。我們可以使用以下程式碼將模型預測的值 ( y_pred ) 與真實值 ( y_test ) 進行比較:
from sklearn.metrics import precision_score
# 計算模型的精確度得分
model_precision = precision_score(y_test, y_pred)
print("Precision:", model_precision)
1.3 混淆矩陣
混淆矩陣是一個表格,總結了分類模型的表現,透過比較預測值和實際值。它為我們提供了一個模型表現的直觀表示,幫助識別模型的錯誤之處。它顯示了我們的所有四個分類結果。混淆矩陣提供了模型效能的直觀表示,並有助於識別模型在哪裡犯了錯誤。
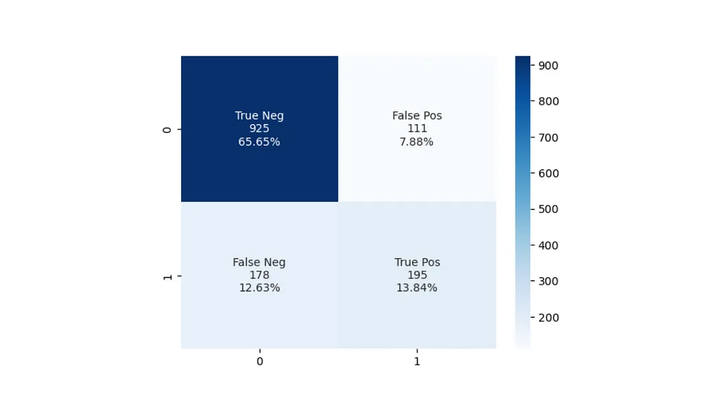
概括:
- 提供真陽性、假陽性、真陰性和假陰性的詳細分類。
- 深入瞭解每個類別的模型效能,有助於識別弱點和偏差。
- 作為計算各種指標的基礎,例如精確度、召回率、F1 分數和準確度。
- 可能更難以解釋和溝通,因為它不提供整體模型效能的單一值(出於比較目的可能需要該值)。
在 Python 中繪製混淆矩陣的一種簡單方法是:
from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay
# 計算混淆矩陣
conf_matrix = confusion_matrix(y_test, y_pred)
# 展示混淆矩陣
disp = ConfusionMatrixDisplay(confusion_matrix=conf_matrix, display_labels=model.classes_)
disp.plot()
1.4 精度 精確度,就是我們模型預測出來的正類中所佔的份額。精度的公式為:
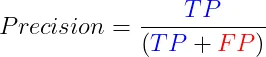
這個指標,特別在那些把假陽性看得比較重的場景下格外重要,比如說過濾垃圾郵件或者是醫學上的診斷。但光有精確度還不夠,因為它沒辦法告訴我們假陰性的情況,所以一般會跟召回率一起搭配使用。 概括:
- 在誤報的代價特別大的情況下,精確度就顯得尤為關鍵了。
- 易於理解和溝通。
- 但它就是不涉及那些被模型錯過的正類,即假陰性的數量。
- 適用於不平衡資料。但是,它應該與其他指標結合使用,因為高精度可能會以犧牲不平衡資料集的召回率為代價
1.5 召回率(靈敏度) 召回率,也叫靈敏度,是評估在所有真正的正例中,有多少被我們的模型正確識別出來的比例。召回率的公式為:
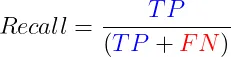
在那些錯過真陽性的代價極其重大的場合——比如癌症篩查或者防範信用詐騙,或是在那種正類相對較少的資料集裡——召回率的重要性不言而喻。正如召回率需要和精確率一樣的搭檔一樣,為了達到一種評估的平衡,召回率也需要和其他指標一併參考。 概括:
- 在錯失真陽性的後果非常嚴重時,召回率顯得格外關鍵。
- 易於理解和溝通。
- 不考慮誤報的數量。
- 適用於不平衡資料。然而,它應該與其他指標結合起來,因為高召回率可能會以犧牲不平衡資料集的精度為代價。
1.6 F1-分數 F1 分數是精確率和召回率的調和平均值,提供了平衡兩者的單一指標。 F1 分數的公式如下:
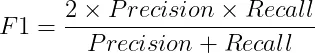
當誤報和漏報同樣重要並且您尋求精確率和召回率之間的平衡時,F1 分數非常有用。 概括:
- F1-Score 平衡精確度和召回率:當誤報和漏報都很重要時很有用。
- 對於不平衡的資料特別有用,在這種情況下,需要在精確度和召回率之間進行權衡。
- 偏向於具有相似精度和召回率的模型,這可能並不總是令人滿意的。
- 可能不足以比較不同模型的效能,特別是當模型在誤報和漏報之間具有不同的權衡時。
一次性獲得準確率、召回率和 F1 分數的最簡單方法是使用 scikit-learn 的分類報告:
from sklearn.metrics import classification_report # 修正匯入語句,應該在import和classification_report之間加上空格
# 生成分類報告
# 該報告包括了精確度、召回率、F1分數等關鍵指標
class_report = classification_report(y_test, y_pred)
# 列印分類報告
print(class_report)
這為我們提供了兩個類別的準確率、召回率和 F1 分數。
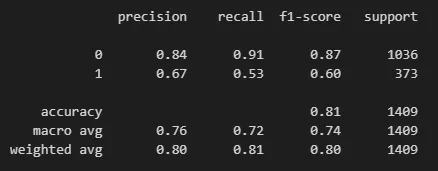
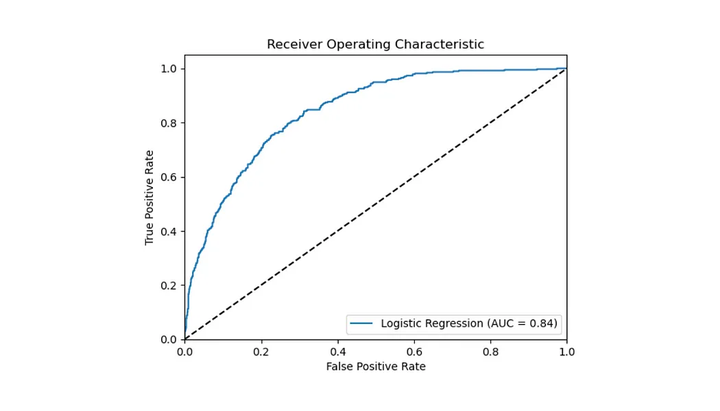
1.7 工作特性曲線下面積(AUC)
AUC衡量的是在不同的判定門檻下,模型識別正類的能力與誤將負類判為正類的風險之間的平衡。AUC值滿分為1,代表模型預測能力無懈可擊,而得分為0.5則意味著模型的預測不過是碰運氣。在評估和比較多個模型的表現時,AUC尤其有價值,但為了深入掌握每個模型在各個方面的優劣,最好還是將它與其他效能指標一併參考。
概括:
- 評估各種分類閾值的模型效能。
- 適用於不平衡的資料集。
- 可用於比較不同模型的效能。
- 假設誤報和漏報具有相同的成本。
- 非技術利益相關者難以解釋,因為它需要了解 ROC 曲線。
- 可能不適合具有少量觀測值的資料集或具有大量類別的模型。
我們可以使用以下程式碼計算 AUC 分數並繪製 ROC 曲線:
# 從sklearn.metrics模組匯入roc_auc_score和roc_curve函式用於計算AUC分數和繪製ROC曲線,同時匯入matplotlib.pyplot用於繪圖
from sklearn.metrics import roc_auc_score, roc_curve
import matplotlib.pyplot as plt
# 使用模型對測試集X_test進行機率預測,取正類預測機率為真陽性率的依據
y_pred_proba = my_model.predict_proba(X_test)[:, 1]
# 利用真實標籤y_test和預測機率y_pred_proba計算AUC分數,評估模型的整體效能
auc_score = roc_auc_score(y_test, y_pred_proba)
# 基於真實標籤和預測機率,計算ROC曲線的假陽性率(fpr)和真陽性率(tpr),及不同閾值
fpr, tpr, Thresholds = roc_curve(y_test, y_pred_proba)
# 使用matplotlib繪製ROC曲線,展示模型的效能。曲線下的面積(AUC)越大,模型效能越好
plt.plot(fpr, tpr, label='My Model (AUC = %0.2f)' % auc_score)
# 繪製對角線,表示隨機猜測的效能水平,作為效能的基準線
plt.plot([0, 1], [0, 1], 'k--')
# 設定影像的x軸和y軸的顯示範圍
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
# 設定x軸標籤為“誤報率”和y軸標籤為“真陽性率”,即ROC曲線的標準軸標籤
plt.xlabel('誤報率')
plt.ylabel('真陽性率')
# 設定圖表標題為“接收器操作特徵”,即ROC曲線的常見名稱
plt.title('接收器操作特徵')
# 新增圖例,位於圖的右下角,展示模型及其AUC分數
plt.legend(loc="lower right")
# 顯示繪製的影像
plt.show()
1.7 對數損失(交叉熵損失) 對數損失用來評估模型預測準確性的一種方法,它對每次預測的正確與否進行獎懲。 這種度量方式透過懲罰錯誤的預測同時獎勵正確的預測來工作。如果對數損失的值越低,意味著模型的效能越好,而當這個值達到0時,就代表這個模型能夠完美地進行分類。
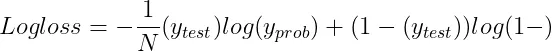
- N是觀測值的數量。
- y_test是二元分類問題的真實標籤(0 或 1)。
- y_prob是標籤為 1 的預測機率。
當你需要對模型的機率預測進行評估時,比如在應用邏輯迴歸或者神經網路模型的情況下,對數損失就顯得尤為重要了。 為了能更深入地掌握模型在各個分類上的表現,最好是將對數損失與其他評估指標一起考慮使用。 概括:
- 機率預測:衡量輸出機率估計的模型的效能,鼓勵經過良好校準的預測。
- 對數損失可用於比較不同模型的效能或最佳化單個模型的效能。
- 適用於不平衡資料。
- 對極端機率預測高度敏感,這可能會導致錯誤分類例項的巨大懲罰值。
- 可能難以向非技術利益相關者解釋和溝通。

2 迴歸指標
2.1 平均絕對誤差(MAE)
平均絕對誤差(MAE)是用來計算預測值和實際值之間差距絕對值的平均量。簡單來說,MAE的計算公式如下:
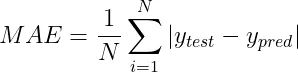
- N是資料點的數量。
- y_pred是預測值。
- y_test是實際值。
概括
- 易於解釋:表示平均誤差大小。
- 對異常值的敏感度低於均方誤差 (MSE)。
- 無錯誤方向:不表示高估或低估。
- 在某些情況下可能無法捕獲極端錯誤的影響。
在 Python 中,使用 scikit-learn:
from sklearn.metrics import mean_absolute_error # 修正函式名稱,應為小寫的 'mean_absolute_error'
# 計算真實值與預測值之間的平均絕對誤差 (MAE)
mae = mean_absolute_error(y_true, y_pred) # 計算MAE
# 列印MAE值,以評估模型預測的準確性
print("MAE:", mae)
2.2 均方誤差(MSE) 均方誤差(MSE)用於計算預測值與實際值差異的平方後的平均數。MSE 的公式為:
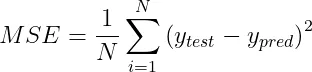
MSE特別對離群值敏感,這是因為它對於較大的誤差施加了更重的懲罰,遠超過小誤差。這一特性根據具體的應用場景,既可能是一個優勢也可能是一個劣勢。 概括:
- 對極端錯誤更加敏感。
- 平方誤差值可能不如絕對誤差直觀。
- 與平均絕對誤差 (MAE) 相比,受異常值的影響更大。
2.3 均方根誤差(RMSE) 均方根誤差 (RMSE) 是均方誤差的平方根。RMSE 的公式為:
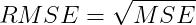
RMSE同樣對離群值敏感,和MSE一樣,對較大的誤差給予較重的懲罰。不過,RMSE的一個顯著優勢在於它的單位和目標變數保持一致,這使得RMSE更加易於理解和解釋。 概括:
- 對極端錯誤更加敏感。
- 與目標變數相同的單位:
- 與平均絕對誤差 (MAE) 相比,受異常值的影響更大。
在 Python 中,使用 scikit-learn:
from sklearn.metrics import mean_squared_error # 注意修正匯入函式名的大小寫
# 利用模型對資料集X進行預測,得到預測值y_pred
y_pred = model.predict(X)
# 計算實際值y和預測值y_pred之間的均方誤差(MSE)
mse = mean_squared_error(y, y_pred) # 注意修正函式名的大小寫
# 透過對MSE取平方根,計算均方根誤差(RMSE),這一步使得誤差單位與目標變數單位一致
rmse = np.sqrt(mse)
# 輸出均方根誤差(RMSE),以評估模型預測的準確性
print('Root Mean Squared Error:', rmse)
2.4 平均絕對百分比誤差(MAPE)
平均絕對百分比誤差(MAPE)是一個衡量預測準確性的指標,它透過計算預測值與實際值之間差異的百分比,然後取這些百分比差異的平均值來實現。MAPE的計算方式可以這樣表達:
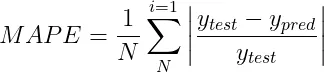
在對比不同模型效能或判斷誤差的重要程度時,MAPE展現了其獨到的價值。 但是,當涉及到接近零的數值時,MAPE的應用就會遇到挑戰,因為這時的百分比誤差可能會激增,變得異常巨大。
概括:
- 相對誤差指標:可用於比較不同尺度的模型效能。
- 易於解釋:以百分比表示。
- 零值未定義,這可能發生在某些應用程式中。
- 不對稱:高估小實際值的誤差,低估大實際值的誤差。
Scikit learn 沒有 MAPE 函式,但我們可以使用以下方法自己計算:
# 定義一個函式來計算平均絕對百分比誤差(MAPE)
def mape(y_true, y_pred):
# 計算真實值與預測值之間的絕對差異,然後除以真實值,最後乘以100轉換為百分比
return np.mean(np.abs((y_true - y_pred) / y_true)) * 100
# 使用定義好的MAPE函式,傳入真實值y_true和預測值y_pred,計算MAPE
mape_value = mape(y_true, y_pred) # 修正變數名以避免與函式名相同
# 列印MAPE值,評估模型預測的平均誤差百分比
print("MAPE:", mape_value) # 修正語法錯誤
2.5 R 平方(決定係數) R平方衡量了模型預測值與實際值之間的一致性,透過計算模型能解釋的目標變數方差的比例來評估。具體來說,R平方的計算公式如下:
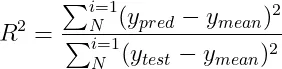
- y_mean是實際值的平均值。
- y_pred是預測值。
- y_test是實際值。
R平方的取值介於0到1之間,其中值越接近1意味著模型的預測能力越強。但是,R平方也存在一定的限制,比如說,即使加入了與目標變數無關的特徵,其值也有可能上升。 概括:
- 代表解釋方差的比例,使其易於理解和溝通。
- 對目標變數的規模不太敏感,這使得它更適合比較不同模型的效能。
- 偏向於具有許多功能的模型,這可能並不總是令人滿意的。
- 不適合評估預測變數和目標變數之間不存線上性關係的模型。
- 可能會受到資料中異常值的影響。
在 Python 中,使用 scikit-learn:
from sklearn.metrics import r2_score
# 使用r2_score函式計算真實值y_true和預測值y_pred之間的R平方值
r_squared = r2_score(y_true, y_pred)
# 輸出R平方值,以評估模型解釋目標變數方差的能力
print("R-squared:", r_squared)
2.6 調整後的 R 平方(Adjusted R-Squared)
Adjusted R-Squared 是對R平方( R-Squared)的改良,它在計算過程中考慮到了模型中包含的特徵數量,從而對模型複雜度進行了調整。調整R平方的計算公式是這樣的:
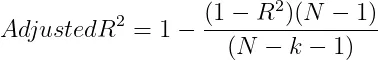
- N是資料點的數量。
- k是特徵的數量。
調整後的 R-Squared 可以透過懲罰具有過多特徵的模型來幫助防止過度擬合。 概括:
- 修改 R 平方,調整模型中預測變數的數量,使其成為比較具有不同預測變數數量的模型效能的更合適的指標。
- 對目標變數的規模不太敏感,這使得它更適合比較不同模型的效能。
- 懲罰額外變數:與 R 平方相比,降低過度擬合風險。
- 不適合評估預測變數和目標變數之間不存線上性關係的模型。
- 可能會受到資料中異常值的影響。
在 Python 中,我們可以根據 R 平方分數來計算它:
from sklearn.metrics import r2_score
# 計算模型的R平方值,即模型的解釋能力
r_squared = r2_score(y, y_pred)
# 為了更準確地評估模型效能,計算調整後的R平方值
heroes_count = len(y) # 觀測值數量,類比為武林中的英雄人數
techniques_count = X.shape[1] # 特徵數量,類比為模型中的武學技巧數
# 調整後的R平方值的計算考慮了模型中的特徵數量
adj_r_squared = 1 - (((1 - r_squared) * (heroes_count - 1)) / (heroes_count - techniques_count - 1))
# 輸出調整後的R平方值
print("調整後的R平方:", adj_r_squared)

3 選擇合適的指標
選擇合適的評估指標對於確保專案成功至關重要。這一選擇應基於具體問題背景、採用的模型型別,以及希望達成的專案目標。以下內容將引導您如何根據這些因素做出明智的決策。
3.1 瞭解問題背景
在選擇指標之前,瞭解專案背景至關重要。考慮以下因素:
- 機器學習任務型別:選擇指標時需要考慮您是在處理分類、迴歸還是多標籤問題,因為不同的問題型別適合不同的評估方法。
- 資料分佈情況:面對不平衡資料時,某些指標(如F1分數、精確度、召回率或AUC)可能更加有效,因為它們對類不平衡的敏感度較低。
- 錯誤的成本:考慮到誤報和漏報在您的應用中可能帶來的後果不同,選擇能夠恰當反映這些錯誤影響的指標十分重要。
3.2 考慮模型目標
模型旨在解決的具體問題同樣影響著指標的選擇:
- 準確機率估計:如果您的模型需要提供精確的機率預測,對數損失是一個很好的選擇。
- 真陽性率與誤報的平衡:若要在提高真陽性率的同時降低誤報,考慮AUC作為評估標準可能更為合適。
3.3 評估多個指標
為了獲得模型效能的全面檢視,建議同時考慮多個指標。這樣不僅可以揭示模型的長處和短板,還能為模型的最佳化提供方向。例如:
- 分類任務:同時考慮精確度、召回率和F1分數,可以幫助您在誤報和漏報之間找到一個平衡點。
- 迴歸任務:結合使用如MAE這樣的絕對誤差指標和MAPE這樣的相對誤差指標,可以從不同角度評估模型的表現。
[ 抱個拳,總個結 ]
我們探討了如何選擇適合評估機器學習模型效能的指標,強調了指標選擇的重要性,並提供了一系列指導原則來幫助你做出明智的選擇。以下是各個關鍵部分的簡要回顧:
- 瞭解問題背景:考慮機器學習任務的型別、資料的分佈以及各種型別錯誤的重要性。
- 考慮模型目標:根據模型旨在解決的具體問題,選擇最合適的指標,如準確機率估計或平衡真陽性率與誤報。
- 評估多個指標:為了全面瞭解模型的效能,建議同時評估多個指標,包括精確度、召回率、F1分數(分類任務),以及MAE、MSE、MAPE(迴歸任務)。
具體到每個指標,我們討論了:
- 分類指標:介紹了分類任務中的基本概念,如真正例、假正例、真反例、假反例,以及衡量這些分類結果的準確度、混淆矩陣、精確度、召回率、F1分數和AUC。
- 迴歸指標:探討了迴歸任務中的關鍵指標,包括平均絕對誤差(MAE)、均方誤差(MSE)、均方根誤差(RMSE)、平均絕對百分比誤差(MAPE)和R平方(決定係數)。
透過選擇正確的驗證指標,可以清晰地評估和最佳化模型效能,確保機器學習專案的成功。希望本指南能夠為你的機器學習之旅提供實用的見解和支援。
