錯誤率:錯分樣本的佔比。如果在m個樣本中有a個樣本分類錯誤,則錯誤率為E=a/m;相應的,1-a/m稱為“精度”,即“精度=1-錯誤率”
誤差:樣本真實輸出與預測輸出之間的差異。
訓練(經驗)誤差:訓練集上;測試誤差:測試集;泛化誤差:除訓練集外所有樣本
過擬合:學習器把訓練樣本學習的“太好”,將訓練樣本本身的特點當作所有樣本的一般性質,導致泛化效能下降。(機器學習面臨的關鍵障礙,優化目標加正則項、early stop)
欠擬合:對訓練樣本的一般性質尚未學好。(決策樹:擴充分支,神經網路:增加訓練輪數)
評估方法:
現實任務中往往會對學習器的泛化效能、時間開銷、儲存開銷、可解釋性等方面的因素進行評估並作出選擇。
通常將包含m個樣本的資料集D={(x1,y1),(x2,y2),...,(xm,ym)}拆分成訓練集S和測試集T:
留出法:
直接將資料集劃分為兩個互斥集合
訓練/測試集劃分要儘可能保持資料分佈的一致性
一般若干次隨機劃分、重複實驗取平均值
訓練/測試樣本比例通常為2:1~4:1
交叉驗證法:
將資料集分層取樣劃分為k個大小相似的互斥子集,每次用k-1個子集的並集作為訓練集,餘下的子集作為測試集,最終返回k個測試結果的均值,k最常用的取值是10.
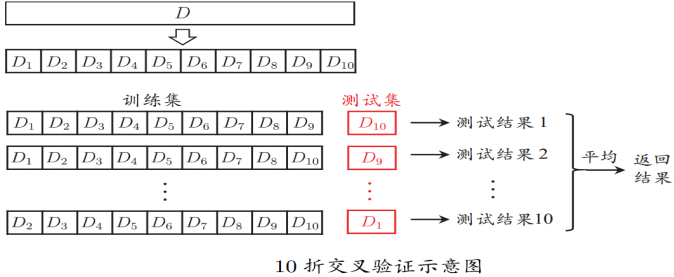
與留出法類似,將資料集D劃分為k個子集同樣存在多種劃分方式,為了減小因樣本劃分不同而引入的差別,k折交叉驗證通常隨機使用不同的劃分重複p次,最終的評估結果是這p次k折交叉驗證結果的均值,例如常見的“10次10折交叉驗證”
假設資料集D包含m個樣本,若令k=m,則得到留一法:
不受隨機樣本劃分方式的影響
結果往往比較準確
當資料集比較大時,計算開銷難以忍受
自助法:
以自助取樣法為基礎,對資料集D有放回取樣m次得到訓練集D',D\D'用做測試集。
實際模型與預期模型都使用m個訓練樣本
約有1/3的樣本沒在訓練集中出現
從初始資料集中產生多個不同的訓練集,對整合學習有很大的好處
自助法在資料集較小、難以有效劃分訓練/測試集時很有用;由於改變了資料集分佈可能引入估計偏差,在資料量足夠時,留出法和交叉驗證法更常用。
評估分類器效能的度量
正元組(正樣本):感興趣的主要類的元組,P是正元組數。
負元組(負樣本):其他元組,N是負元組數。
混淆矩陣(confusion matrix):
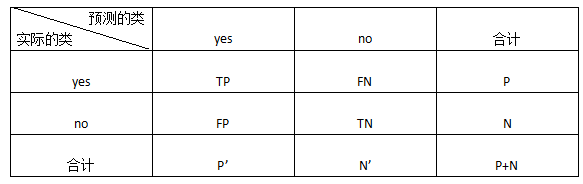
TP(True Positive):真正例/真陽性,是指被分類器正確分類的正元組
TN(True Negative):真負例/真陰性,是指被分類器正確分類的負元組
FP(False Positive):假正例/假陽性,是被錯誤地標記為正元組的負元組
FN(False Negative):假負例/假陰性,是被錯誤地標記為負元組的正元組
P’:被分類器標記為正的元組數(TP+FP)
N’:被分類器標記為負的元組數(TN+FN)
元組的總數=TP+TN+FP+FN=P+N=P'+N’
準確率(accuracy):被分類器正確分類的元組所佔的百分比,準確率又稱為分類器的總體識別率,即它反映分類器對各類元組的正確識別情況,當類分佈相對平衡時最有效。即
accuracy=(TP+TN)/(P+N)
錯誤率(error rate,誤分類率):error rate=(FP+FN)/(P+N)=1-accuracy
靈敏性(sensitivity)、真正例率(正確識別的正元組的百分比):sensitivity=TP/P
特效性(specificity)、真負例率(正確識別的負元組的百分比):specificity=TN/N
準確率是靈敏性和特效性度量的函式:accuracy=(TP+TN)/(P+N)=TP/(P+N)*(P/P)+TN/(P+N)*(N/N)=sensitivity*P/(P+N)+specificity*N/(P+N)
精度(precision):可以看作精確性的度量(標記為正類的元組實際為正類所佔的百分比) precision=TP/(TP+FP)
召回率(recall):完全性的度量(正元組標記為正的百分比),就是靈敏度 recall=TP/(TP+FN)=TP/P=sensitivity

除了基於準確率的度量外,還可以根據其他方面比較分類器:
速度:涉及產生和使用分類器的計算開銷
魯棒性:這是假定資料有噪聲或有缺失值時分類器做出正確預測的能力。通常,魯棒性用噪聲和缺失值漸增的一系列合成資料集評估。
可伸縮性:這涉及給定大量資料,有效地構造分類器的能力。通常,可伸縮性用規模漸增的一系列資料集評估。
可解釋性:這涉及分類器或預測器提供的理解和洞察水平。可解釋性是主觀的,很難評估。
當資料類比較均衡地分佈時,準確率效果最好,其他度量,如靈敏度(或召回率)、特效性、精度、F和Fβ更適合不平衡問題。
P-R曲線
查準率-查全率曲線,以查準率為縱軸,查全率為橫軸作圖。
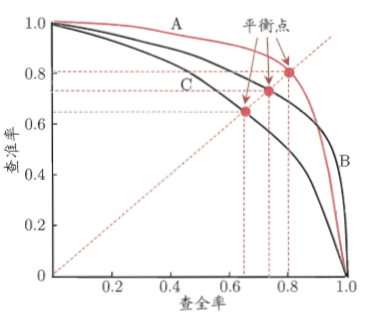
若一個學習器的P-R曲線被另一個學習器的曲線完全“包住”,則後者效能優於前者,上圖中學習器A的效能優於學習器C;如果兩個學習器的P-R曲線發生了交叉,則需要比較P-R曲線下面積的大小,但這個面積不容易估算,通常綜合考慮查準率、查全率的效能度量“平衡點(Break-Event Point,BEP)”,它是“查準率=查全率”時的取值。但BEP還是過於簡化,更常用的是前面提到的F1度量。
ROC與AUC
“最可能”是正例的樣本排在最前面,“最不可能”是正例的排在最後面,按此排序。分類的過程就相當於在排序中以某個“截斷點(cut point)”將樣本分為兩部分,前一部分判斷正例,後一部分為反例。不同任務中根據需求劃分截斷點;重視查準率(精度),靠前位置截斷;重視查全率(召回率),靠後位置截斷。
ROC(Receiver Operating Characteristic,受試者工作特徵)曲線是一種比較兩個分類模型有用的視覺化工具。ROC曲線顯示了給定模型的真正例率(TPR)和假正例率(FPR)之間的權衡,縱軸是“真正例率(TPR)”,橫軸是“假正例率(FPR)”。

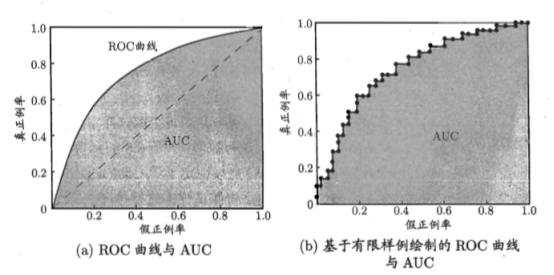
圖(a)中,給出了兩條線,ROC曲線給出的是當閾值變化時假正例率和真正例率的變化情況。左下角的點所對應的是將所有樣例判為反例的情況,而右上角的點對應的則是將所有樣例判為正例的情況。虛線給出的是隨機猜測的結果曲線。
現實任務中通常利用有限個測試樣例來繪製ROC圖,此時僅能獲得有限個(真正例率,假正例率)座標對,無法產生圖(a)中光滑的ROC曲線,只能繪製如圖(b)所示的近似ROC曲線。
繪圖過程:給定m+個正例和m-個反例,根據學習器預測結果對樣例進行排序,然後把分類閾值設為最大,即把所有樣例均預測為反例,此時真正例率和假正例率均為0,在座標(0,0)處標記一個點。然後,將分類閾值依次設為每個樣例的預測值,即依次將每個樣例劃分為正例。設前一個標記點座標為(x,y),當前若為真正例,則對應標記點的座標為(x,y+1/m+);當前若為假正例,則對應標記點的座標為(x+1/m-,y),然後用線段連線相鄰點即可。
若一個學習器的ROC曲線被另一個學習器的曲線完全“包住”,則可斷言後者效能優於前者;如果曲線交叉,可以根據ROC曲線下面積大小進行比較,也即AUC(Area Under ROC Curve)值.
AUC可通過對ROC曲線下各部分的面積求和而得。假定ROC曲線由座標為{(x1,y1),(x2,y2),...,(xm,ym)}的點按序連線而形成(x1=0,xm=1),則AUC可估算為
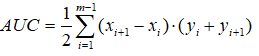
AUC給出的是分類器的平均效能值,它並不能代替對整條曲線的觀察。一個完美的分類器的AUC為1.0,而隨機猜測的AUC值為0.5
AUC考慮的是樣本預測的排序質量,因此它與排序誤差有緊密聯絡。給定m+個正例,m-個反例,令D+和D-分別表示正、反例集合,則排序”損失”定義為
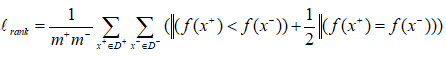
Lrank對應ROC曲線之上的面積:若一個正例在ROC曲線上標記為(x,y),則x恰是排序在期前的所有反例所佔比例,即假正例,因此:
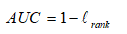
AUC值是一個概率值,當你隨機挑選一個正樣本以及負樣本,當前的分類演算法根據計算得到的Score值將這個正樣本排在負樣本前面的概率就是AUC值,AUC值越大,當前分類演算法越有可能將正樣本排在負樣本前面,從而能夠更好地分類。
代價敏感錯誤率和代價曲線
現實任務中不同型別的錯誤所造成的後果很可能不同,為了權衡不同型別錯誤所造成的不同損失,可為錯誤賦予“非均等代價”。
以二分類為例,可根據領域知識設定“代價矩陣”,如下表所示,其中costij表示將第i類樣本預測為第j類樣本的代價。一般來說,costii=0;若將第0類判別為第1類所造成的損失更大,則cost01>cost10;損失程度越大,cost01與cost10值的差別越大。
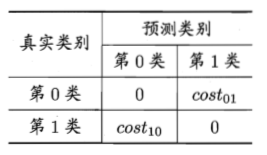
在非均等代價下,不再最小化錯誤次數,而是最小化“總體代價”,則“代價敏感”錯誤率相應的為:
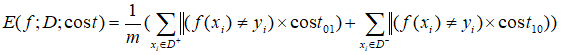
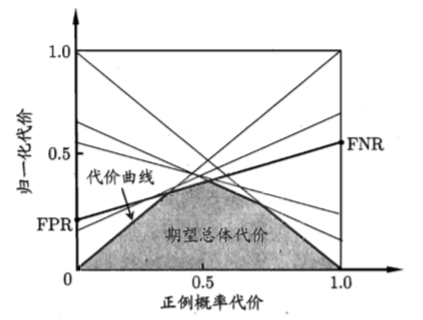
在非均等代價下,ROC曲線不能直接反映出學習器的期望總體代價,而“代價曲線(cost curve)”可以。代價曲線圖的橫軸是取值為[0,1]的正例概率代價
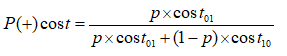
其中p是樣例為正例的概率;縱軸是取值為[0,1]的歸一化代價
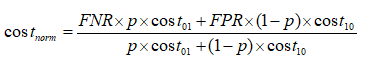
其中FPR是假正例率,FNR=1-TPR是假反例率。
代價曲線的繪製:ROC曲線上每個點對應了代價曲線上的一條線段,設ROC曲線上點的座標為(TPR,FPR),則可相應計算出FNR,然後在代價平面上繪製一條從(0,FPR)到(1,FNR)的線段,線段下的面積即表示了該條件下的期望總體代價;如此將ROC曲線上的每個點轉化為代價平面上的一條線段,然後取所有線段的下界,圍成的面積即為所有條件下學習器的期望總體代價。