雜湊

樹狀陣列是個好東西，寫起來也相對好看。但是操作比較侷限，區間修改就掉回\(O(nlogn)\)， 那還不如 \(O(n)\)。線段樹完美的解決問題。

線段樹，也可以理解的一堆線段組成的樹。

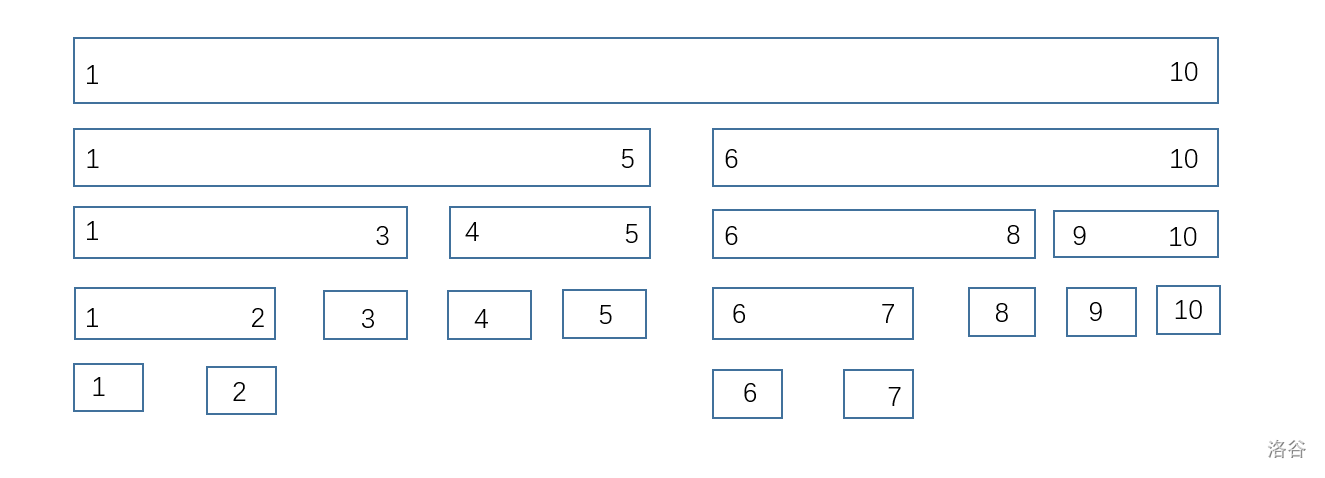
大致如上，有一線段 \([l, r]\) 當 \(l \ne r\) 可化為 \([l, mid]\) , \([mid + 1, r]\)

PS: \(mid = (l + r) / 2\)

增加

此操作 不是 新加節點，是將一段區間增加一個數。

將 [2, 9] 每個數增加 1

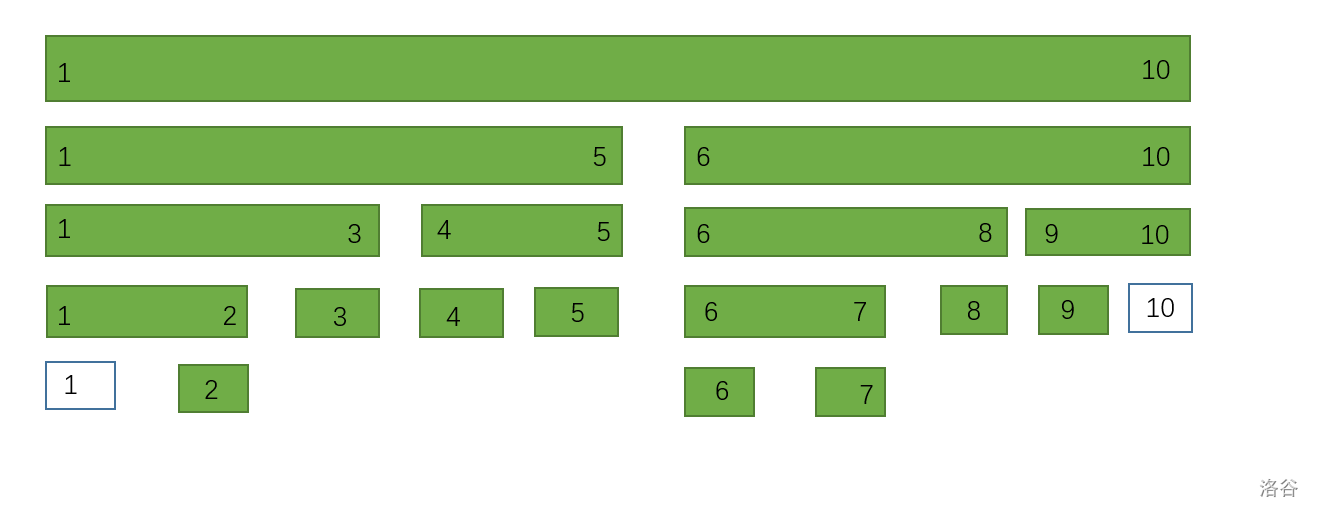
像這樣透過遞迴的方式修改這些節點，然後我們驚喜的發現，訪問了 \(n logn\) 個節點......似乎不如沒有

這個時候lazy_tag登場（懶人tag）

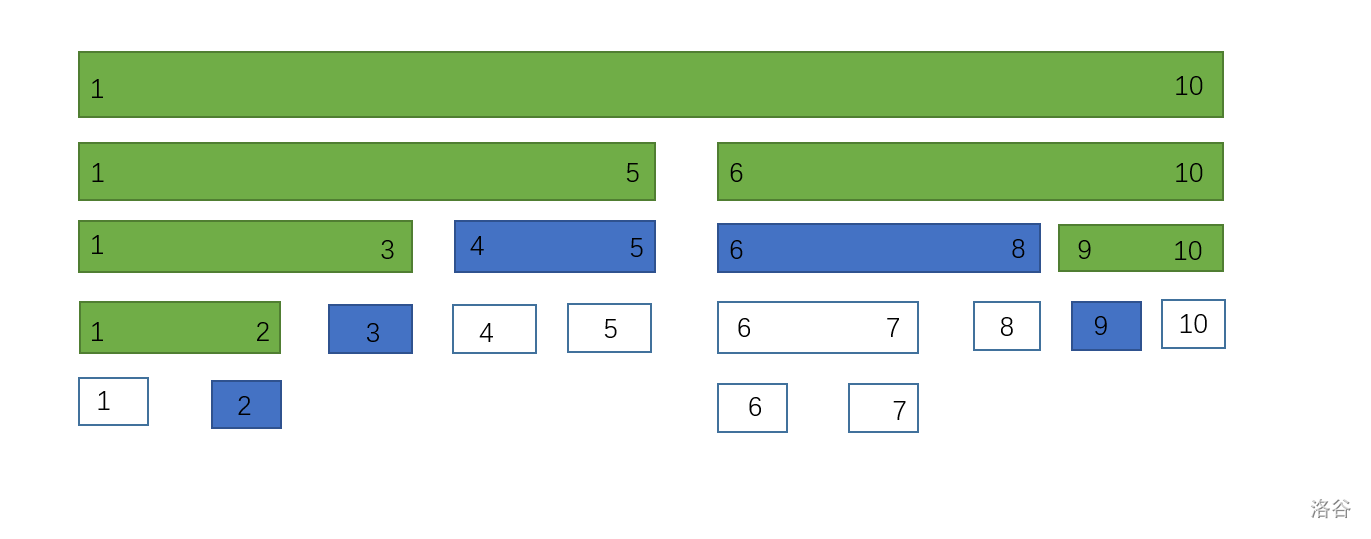
藍色的就是lazy_tag(下文稱為tag)，標記增加了多少， 這時 \([2,2], [3,3],[4,5], [6,8], [9,9]\) 都有 tag = 1。

用處放到下文

查詢

這裡，我們可以查詢區間的和

在上例子裡我們查詢 [1, 1]時，不會有問題，查詢 [1, 2]時，不會有問題， 查詢 [1, 10]時，不會有問題， 但是查詢 [6, ]7時，會有問題， 因為沒有修改到。

因為 [6, 8] 被標有tag， 然而，在訪問 [6, 7]時一定會訪問到6, 8，那麼我們便可以將tag傳下來。

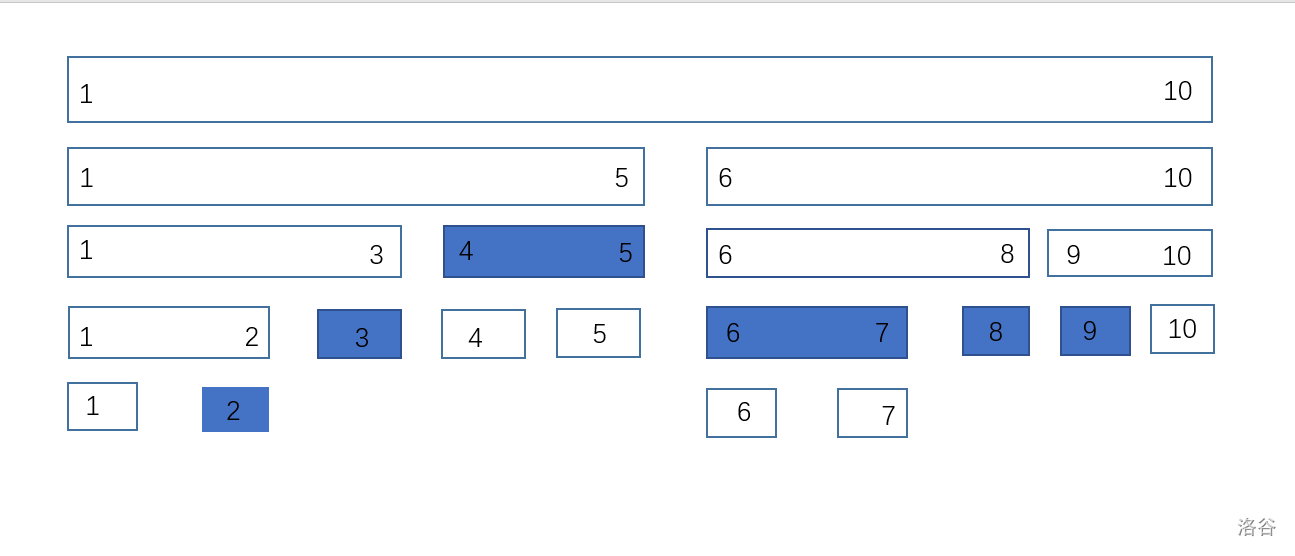
也就是不訪問就不修改。

運用以上方案，就可以實現單點修改，單點查詢，區間修改（同增同減）， 區間查詢。

#include<iostream>

using namespace std;

const long long kMaxN = 1e5 + 5; 

long long n, m, a[kMaxN << 2]; //注意開大4倍

struct L {
	long long sum, tag;
} sgt[kMaxN << 2];

void push_up(long long rt) { //更新這個節點
	sgt[rt].sum = sgt[rt << 1].sum + sgt[rt << 1 | 1].sum;
}	


void build_tree(long long rt, long long l, long long r) { //建樹
	sgt[rt].tag=0;
	if (l == r) {
		sgt[rt].sum = a[l];
		return;
	}
	long long mid = l + r >> 1; 
	build_tree(rt << 1, l, mid), build_tree(rt << 1 | 1, mid + 1, r);
	push_up(rt);
}

void add_tag(long long rt, long long l, long long r,long long d) {//建立tag
	sgt[rt].tag += d;
	sgt[rt].sum += d * (r - l + 1);//值也增加
}

void push_down(long long rt, long long l, long long r) { //tag往下傳
	if (sgt[rt].tag) {
		long long mid = l + r >> 1;
		add_tag(rt << 1, l, mid, sgt[rt].tag);
		add_tag(rt << 1 | 1, mid + 1, r, sgt[rt].tag);
		sgt[rt].tag = 0;
	}
}

void update(long long L, long long R, long long rt, long long l, long long r, long long d){ //更新[l, r]的值 + d
	if (L <= l && r <= R) {
		add_tag(rt, l, r, d);
		return;
	}
	push_down(rt, l, r);
	long long mid = l + r >> 1;
	if (L <= mid) {
		update(L, R, rt << 1, l, mid, d);
	} if (mid < R) {
		update(L, R, rt << 1 | 1, mid + 1, r, d);
	}
	push_up(rt);
} 

long long query(long long L, long long R, long long rt, long long l, long long r) {//找到 [L, R] 的和
	if (L <= l && r <= R) {
		return sgt[rt].sum;
	}
	push_down(rt, l, r);
	long long mid = l + r >> 1, ans = 0;
	if (L <= mid) {
		ans += query(L, R, rt << 1, l, mid);
	} 
	if (mid < R) {
		ans += query(L, R, rt << 1 | 1, mid + 1, r);
	}
	return ans;
}

int main(){
	cin >> n >> m;
	for (long long i = 1; i <= n; i++) {
		cin >> a[i];
	}
	build_tree(1, 1, n);
	for(long long i = 1, a, x, y, d; i <= m; i++) {
		cin >> a >> x >> y;
		if (a == 1) {
			cin >> d;
			update(x, y, 1, 1, n, d);
		} else {
			cout << query(x, y, 1, 1, n) << '\n';
		}
	}
	return 0;
}