X 國王有一個地宮寶庫,是 n×m 個格子的矩陣,每個格子放一件寶貝,每個寶貝貼著價值標籤。
地宮的入口在左上角,出口在右下角。
小明被帶到地宮的入口,國王要求他只能向右或向下行走。
走過某個格子時,如果那個格子中的寶貝價值比小明手中任意寶貝價值都大,小明就可以拿起它(當然,也可以不拿)。
當小明走到出口時,如果他手中的寶貝恰好是 k 件,則這些寶貝就可以送給小明。
請你幫小明算一算,在給定的局面下,他有多少種不同的行動方案能獲得這 k 件寶貝。
輸入格式
第一行 3 個整數,n,m,k,含義見題目描述。
接下來 n 行,每行有 m 個整數 Ci 用來描述寶庫矩陣每個格子的寶貝價值。
輸出格式
輸出一個整數,表示正好取 k 個寶貝的行動方案數。
該數字可能很大,輸出它對 1000000007 取模的結果。
資料範圍
1≤n,m≤50,
1≤k≤12,
0≤Ci≤12
輸入樣例1:
2 2 2
1 2
2 1
輸出樣例1:
2
輸入樣例2:
2 3 2
1 2 3
2 1 5
輸出樣例2:
14
題解:
dp分析:
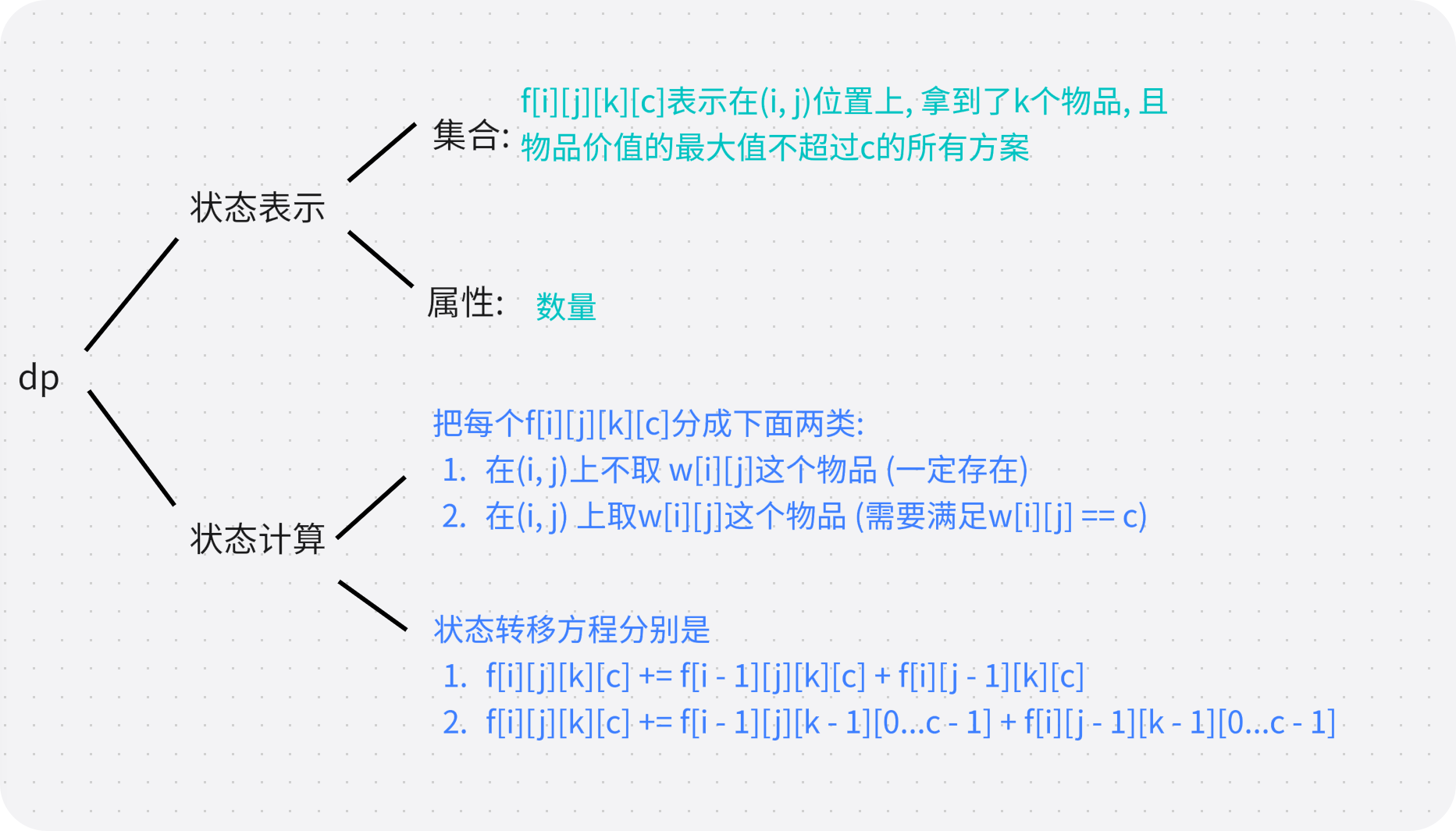
常見問題: 為什麼取第(i,j)物品的時候要滿足 c == w[i][j] ? 以及為什麼狀態轉移方程2 為什麼是0...c累加
- 我們原本定義了f[i][j][k][c]表示的是 在第(i, j)上的, 取了k個物品且這k個物品的最大值不超過c, 這裡我們假設把f[i][j][k][c]表示成 在第(i, j)上的, 取了k個物品且這k個物品的最大值等於c, 這時候需要滿足(w[i][j] == c)應該能理解吧。
- 那我們要想讓我們假設的變成原本表示的含義, 需要讓 f[i][j][k][c] 累加上 f[i][j][k][t] t要滿足小於c, 這樣我們f[i][j][k][c]表示的集合就從假設的變成了原本的, 但是如果f[i][j][k][c]不滿足假設的含義, 那麼我們沒法讓f[i][j][k][c]表示成原本的含義
- 所以取(i,j)上的物品是要滿足(w[i][j]==c) 是為了能夠更好的計算出正確含義的f[i][j][k][c]的值
Orz筆者是這麼理解的~
詳細的狀態轉移如下圖:
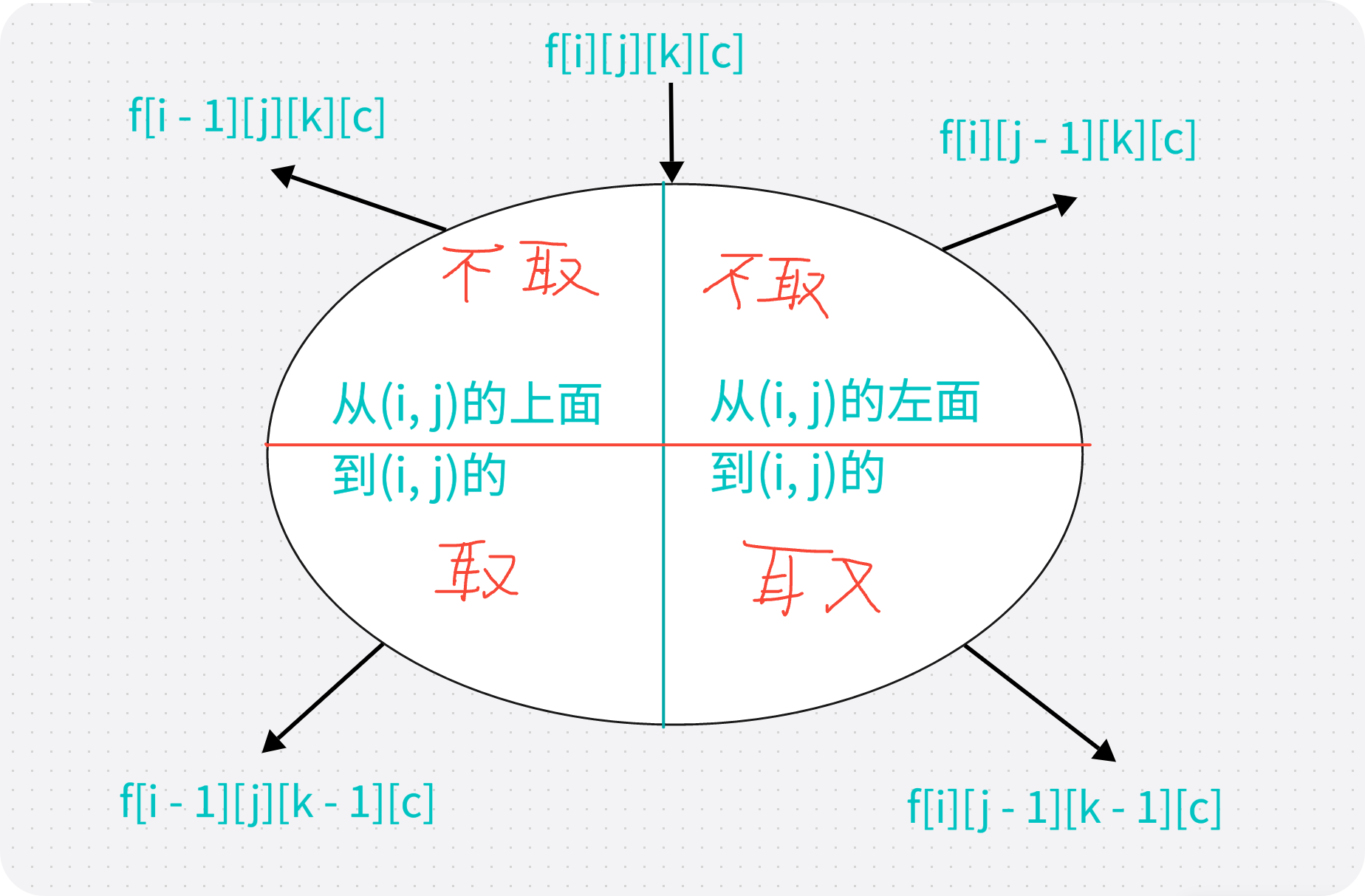
注意事項:
我們f陣列的第四維是代表 最大值不超過c, 但是題中 c = [0,12], 由於當我們沒有選擇任何一個物品的時候應該表示成-1, 但是下標沒法是負的, 所以我們可以把每個 c 都加1, 也就是w[i][j] + 1. 這樣我們 f 的第四維在沒有取任何物品時就可以用 下標 0 表示了
看不懂的話, 可以先看這兩個題, 摘花生 和 最長上升子序列, 本題是前兩道題的揉和
ac程式碼👇
#include <bits/stdc++.h>
using namespace std;
const int N = 55, MOD = 1000000007;
int w[N][N], n, m, k;
int f[N][N][13][14];
int main()
{
cin >> n >> m >> k;
for (int i = 1; i <= n; i ++)
for (int j = 1; j <= m; j ++) cin >> w[i][j], w[i][j] ++;
// 初始化
f[1][1][1][w[1][1]] = 1; // 取
f[1][1][0][0] = 1; // 不取
for (int i = 1; i <= n; i ++)
for (int j = 1; j <= m; j ++)
{
if (i == 1 && j == 1) continue; // 初始話的跳過
for (int u = 0; u <= k; u ++)
for (int v = 0; v <= 13; v ++)
{
f[i][j][u][v] = (f[i][j][u][v] + f[i][j - 1][u][v]) % MOD; // 狀態計算 1
f[i][j][u][v] = (f[i][j][u][v] + f[i - 1][j][u][v]) % MOD; // 狀態計算 2
if (u > 0 && w[i][j] == v) // u > 0 加不加都行, 不影響答案, 因為 u == 0的時候表示什麼都沒選, 進入下面的迴圈也沒意義
{
for (int c = 0; c < v; c ++) // 常見問題解釋的就是這裡, 需要加上比 v 小的f, 才能讓 f[i][j][k][c]表示的含義正確
{
f[i][j][u][v] = (f[i][j][u][v] + f[i][j - 1][u - 1][c]) % MOD; // 狀態計算 3
f[i][j][u][v] = (f[i][j][u][v] + f[i - 1][j][u - 1][c]) % MOD; // 狀態計算 4
}
}
}
}
int res = 0;
for (int i = 0; i <= 13; i ++) res = (res + f[n][m][k][i]) % MOD;
cout << res << endl;
return 0;
}
覺得寫的不錯的話, 點個贊吧~