Codeforces Round 932 (Div. 2) ABCD

Lu_xZ發表於2024-03-06

A. Entertainment in MAC

題意：給定字串 \(S\)，有兩種操作，每次操作其中之一：

  • 把 \(S\) 變為 \(S\) 的翻轉 \(T\)。
  • 把 \(S\) 變為 \(S + T\)。

問操作恰好 \(n\) 次能得到的最小字典序，\(n\) 為偶數。
候選字串的字首要麼是 \(S\)，要麼是 \(T\)，字首相同而長度更長肯定不優，因此 \(ans = min(S, T + S)\)。

void solve() {
	cin >> n >> s;
	t = s;
	ranges::reverse(t);
	if(t < s) cout << (t + s) << '\n';
	else cout << s << '\n';
}

B. Informatics in MAC

題意：給定陣列 \(a\)，劃分為若干段（大於 \(1\) ），求一種劃分方式，使得每段的 \(mex\) 相同，或者不存在。
\(mex\) 相同的兩段合併後 \(mex\) 不變。
於是問題轉化為：把陣列分為兩段，使得每段 \(mex\) 相同。
預處理字首以及字尾 \(mex\)，列舉劃分位置。

void solve() {
	int n; cin >> n; vector<int> a(n + 1);
	
	rep(i, 1, n) cin >> a[i];
	
	vector<int> pre(n + 1, 0), suf(n + 1, 0);
	set<int> se;
	rep(i, 0, n) se.insert(i);
	rep(i, 1, n) {
		if(se.find(a[i]) != end(se)) {
			se.erase(a[i]);
		}
		pre[i] = *begin(se);
	}
	rep(i, 0, n) se.insert(i);
	per(i, n, 1) {
		if(se.find(a[i]) != end(se)) {
			se.erase(a[i]);
		}
		suf[i] = *begin(se);
	}
	rep(i, 2, n) {
		if(pre[i - 1] == suf[i]) {
			cout << 2 << '\n';
			cout << 1 << ' ' << i - 1 << '\n';
			cout << i << ' ' << n << '\n';
			return;
		}
	}
	cout << -1 << '\n';
}

C. Messenger in MAC

題意：給定 \(n\) 對 \((a, b)\)，選出 \(k\) 對資料並任意排列。
一個長度為 \(k\) 的排列的代價如下定義：

\[\sum_{i=1}^{k} a_{p_i} + \sum_{i=1}^{k - 1} |b_{p_i} - b_{p_{i+1}}| \]

\(p\) 為各元素在排列中的位置。

在貢獻不大於 \(m\) 的情況下，最大化 \(k\)。


如果我們已經確定了所選元素，如何最小化代價。
$ \sum a$ 不會隨順序變化。
對於 \(b\)，可以當做遍歷數軸上的 \(k\) 個點所走的路程。

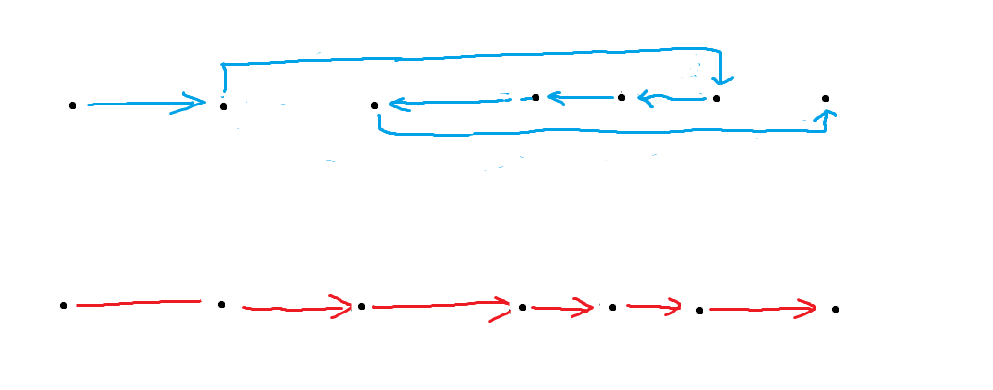
可以直觀的看到，對 \(b\) 排序後最優。

因此，所有數先按 \(b\) 排序。
令 \(f[i][j]\) 表示選 \(i\) 個元素，最後一個元素是 \(j\) 的最小代價。
有

\[f[i][j] = f[i - 1][k] + a[j] + (b[j] - b[k]) \ \ \ \ \ \ \ \ k < j \]

直接轉移是 \(O(n^3)\) 的，考慮字首 \(min\) 最佳化。
令

\[g[i][j] = min(f[i][k] - b[k]) \ \ \ \ \ \ \ \ 1 \le k \le j \]

所以

\[f[i][j] = g[i - 1][j - 1] + a[j] + b[j] \]

struct Node {
	int a, b;
	bool operator < (const Node &o) const {
		return b < o.b;
	}
};

void solve() {
	int n, m; cin >> n >> m;
	vector<Node> t(n + 1);
	rep(i, 1, n) {
		cin >> t[i].a >> t[i].b;
	}
	sort(All(t));
	
	vector<vector<ll>> f(n + 1, vector<ll>(n + 1, 1e18));
	int ans = 0;
	
	rep(i, 1, n) {
		if(t[i].a <= m) {
			ans = 1;
		}
		f[1][i] = min(f[1][i - 1], (ll)t[i].a - t[i].b);
	}
	
	rep(i, 2, n) {
		rep(j, i, n) {
			f[i][j] = f[i - 1][j - 1] + t[j].a + t[j].b;
		}
		rep(j, i, n) {
			if(f[i][j] <= m) {
				ans = i;
			}
			f[i][j] = min(f[i][j - 1], f[i][j] - t[j].b);
		}
	}
	cout << ans << '\n';
	
}

D. Exam in MAC

題意：給定一個大小為 \(n\) 的不可重集 \(s\) 和整數 \(c\)，統計滿足以下所有條件的 \((x, y)\) 對數。

  • \(0 \leq x \leq y \leq c\)
  • \(x + y\) 不在集合內。
  • \(y - x\) 不在集合內。

簡單的容斥。
\(Ans = U - \{x + y \in s\} - \{y - x \in s\} + \{x + y \in s\} \cap \{y - x \in s\}\)

最後一部分的交集的充要條件為兩元素奇偶性相同，直接統計即可。

void solve() {
	ll n, c; cin >> n >> c;
	ll ans = (c + 2) * (c + 1) / 2;
	int cnt[2] = {0, 0};
	rep(i, 1, n) {
		int x; cin >> x;
		ans -= (x / 2 + 1);
		ans -= (c - x + 1);
		ans += ++ cnt[x & 1];
	}
	cout << ans << '\n';
}

相關文章