A. Make All Equal
簽到題，先確定最終答案，然後把其他數刪去，轉化為統計眾數
點選檢視程式碼
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
int read()
{
int x = 0; bool f = false; char c = getchar();
while(c < '0' || c > '9') f |= (c == '-'), c = getchar();
while(c >= '0' && c <= '9') x = (x << 1) + (x << 3) + (c & 15), c = getchar();
return f ? -x : x;
}
const int N = 105;
int a[N], cnt[N];
int main()
{
int T = read();
while(T--)
{
int n = read(), ans = 0x3f3f3f3f;
for(int i = 1; i <= n; ++i)
{
a[i] = read();
++cnt[a[i]];
}
for(int i = 1; i <= n; ++i) ans = min(ans, n - cnt[i]);
for(int i = 1; i <= n; ++i) --cnt[a[i]];
printf("%d\n", ans);
}
return 0;
}
B. Generate Permutation
神奇構造題，透過手動列舉 \(n = 1,2,3,4\) 大膽猜測奇數有解偶數無解，並按照如下構造
\[1,3,5,\cdots n - 2,n,n-1,\cdots,4,2
\]
點選檢視程式碼
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
int read()
{
int x = 0; bool f = false; char c = getchar();
while(c < '0' || c > '9') f |= (c == '-'), c = getchar();
while(c >= '0' && c <= '9') x = (x << 1) + (x << 3) + (c & 15), c = getchar();
return f ? -x : x;
}
const int N = 105;
int a[N], cnt[N];
int main()
{
int T = read();
while(T--)
{
int n = read();
if(n % 2 == 1)
{
int pos = (n + 1) / 2, now = n - 1;
for(int i = 1; i <= pos; ++i) printf("%d ", 2 * i - 1);
for(int i = pos + 1; i <= n; ++i, now -= 2) printf("%d ", now);
printf("\n");
}else printf("-1\n");
}
return 0;
}
C. Guess The Tree
第一次場切互動題！
觀察到最多 \(15n\) 次詢問，考慮一個 \(\log\) 的做法，二分！
依照 \(\text{prim}\) 演算法，最初令 \(1\) 為樹根，並逐步將其他點連線到樹上
定義函式 \(get(l, r)\) 表示將 \(l, r\) 相連，並記錄其中的邊
考慮詢問 \((l, r)\) 的結果 \(x\)：
若 \(x = l\) ，說明 \(l, r\) 直接相連，將 \(r\) 加入樹並向答案中加入邊 \((l, r)\)
若 \(x \neq l\) ，說明 \(l\) 到 \(r\) 的路徑上還有其他點 \(x\) ，若 \(x\) 未加入樹，遞迴相連 \(l, x\) ；若 \(r\) 未加入樹，遞迴相連 \(x, r\)
連線一條邊的均攤複雜度為 \(\log n\)
點選檢視程式碼
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
int read()
{
int x = 0; bool f = false; char c = getchar();
while(c < '0' || c > '9') f |= (c == '-'), c = getchar();
while(c >= '0' && c <= '9') x = (x << 1) + (x << 3) + (c & 15), c = getchar();
return f ? -x : x;
}
const int N = 1005;
int vis[N], cnt = 0;
vector< pair<int, int> > ans;
void get(int l, int r)
{
printf("? %d %d\n", l, r);
fflush(stdout);
int mid = read();
if(mid == l)
{
vis[l] = vis[r] = 1;
ans.push_back(pair<int, int>(l, r));
return ;
}
if(!(vis[l] && vis[mid])) get(l, mid);
if(!(vis[r] && vis[mid])) get(mid, r);
}
int main()
{
int T = read();
while(T--)
{
int n = read();
cnt = 0;
for(int i = 0; i <= n; ++i) vis[i] = 0;
ans.clear();
get(1, n);
for(int i = 2; i < n; ++i) if(!vis[i]) get(1, i);
printf("! ");
for(auto it = ans.begin(); it != ans.end(); ++it)
printf("%d %d ", (*it).first , (*it).second );
printf("\n");
fflush(stdout);
}
return 0;
}
D. Longest Max Min Subsequence
首先想到最多的個數就是數字的種類數，再考慮如何最小化字典序
大膽猜測這是一個貪心，一個位置 \(i\) （值為 \(val\)）能夠被選擇要滿足兩個要求：
-
在此之前沒有選擇過值為 \(val\) 的位置
-
選擇位置 \(i\) 不會減少答案
記 \(last[i]\) 表示數值 \(i\) 在序列中最後出現的位置
每次在當前能選擇的位置中選擇能最小化字典序的位置，若值相同優先選位置小的
思路簡單，實現卻是另一回事
賽時用 \(set\) 維護 \(last\) 陣列，然後就是求一個區間內的 \(\min/\max\) ，直接莽線段樹
以及，因為一些值只出現了一次，我給它單獨處理了！實際上按照 \(last\) 維護它不影響正確性
賽後改出來的依託答辯
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
int read()
{
int x = 0; bool f = false; char c = getchar();
while(c < '0' || c > '9') f |= (c == '-'), c = getchar();
while(c >= '0' && c <= '9') x = (x << 1) + (x << 3) + (c & 15), c = getchar();
return f ? -x : x;
}
const int inf = 0x3f3f3f3f;
const int N = 3e5 + 5;
int n, a[N], cnt[N], last[N];
vector<int> pos[N];
set<int> S;
set<int> Q;
#define ls(x) (x << 1)
#define rs(x) (x << 1 | 1)
struct node1
{
int mx, pos;
node1(){ mx = pos = 0; }
node1 friend operator + (node1 a, node1 b)
{
node1 c;
if(a.mx >= b.mx )
{
c.mx = a.mx ;
c.pos = a.pos;
}else
{
c.mx = b.mx ;
c.pos = b.pos;
}
return c;
}
}mx[N << 2];
struct node2
{
int mn, pos;
node2(){ mn = pos = 0; }
node2 friend operator + (node2 a, node2 b)
{
node2 c;
if(a.mn <= b.mn )
{
c.mn = a.mn ;
c.pos = a.pos;
}else
{
c.mn = b.mn ;
c.pos = b.pos;
}
return c;
}
}mn[N << 2];
void pushup(int k)
{
mx[k] = mx[ls(k)] + mx[rs(k)];
mn[k] = mn[ls(k)] + mn[rs(k)];
}
void build(int k, int l, int r)
{
if(l == r){ mx[k].mx = mn[k].mn = a[l], mx[k].pos = mn[k].pos = l; return ; }
int mid = (l + r) >> 1;
build(ls(k), l, mid), build(rs(k), mid + 1, r);
pushup(k);
}
void update(int k, int l, int r, int pos)
{
mx[k].mx = -inf, mn[k].mn = inf, mx[k].pos = mn[k].pos = 0;
if(l == r) return ;
int mid = (l + r) >> 1;
if(pos <= mid) update(ls(k), l, mid, pos);
else update(rs(k), mid + 1, r, pos);
pushup(k);
}
node1 querymax(int k, int l, int r, int L, int R)
{
if(L <= l && r <= R) return mx[k];
int mid = (l + r) >> 1;
if(R <= mid) return querymax(ls(k), l, mid, L, R);
if(L > mid) return querymax(rs(k), mid + 1, r, L, R);
return querymax(ls(k), l, mid, L, R) + querymax(rs(k), mid + 1, r, L, R);
}
node2 querymin(int k, int l, int r, int L, int R)
{
if(L <= l && r <= R) return mn[k];
int mid = (l + r) >> 1;
if(R <= mid) return querymin(ls(k), l, mid, L, R);
if(L > mid) return querymin(rs(k), mid + 1, r, L, R);
return querymin(ls(k), l, mid, L, R) + querymin(rs(k), mid + 1, r, L, R);
}
int ans[N];
int vis[N];
int P = 1, op = 1;
int main()
{
int T = read();
while(T--)
{
n = read();
for(int i = 0; i <= n; ++i)
{
cnt[i] = last[i] = 0, pos[i].clear();
vis[i] = 0;
}
S.clear(), Q.clear();
P = 1, op = 1;
for(int i = 1; i <= n; ++i)
{
a[i] = read();
++cnt[a[i]];
pos[a[i]].push_back(i);
if(cnt[a[i]] >= 2) last[a[i]] = i;
}
build(1, 1, n);
int m = 0, tot = 0;
for(int i = 1; i <= n; ++i)
if(last[i]) S.insert(last[i]);
for(int i = 1; i <= n; ++i)
{
if(cnt[i] > 0) ++m; // 值域
if(cnt[a[i]] == 1)
{
Q.insert(i); // 下標
update(1, 1, n, i);
}
}
Q.insert(n + 1);
while(P <= n && tot < m)
{
if(cnt[a[P]] == 1)
{
ans[++tot] = a[P];
Q.erase(P);
++P;
op ^= 1;
continue;
}
if(vis[P]){ ++P; continue; }
int nx = min(*Q.begin() - 1, *S.begin());
// printf("P = %d, nx = %d, S.begin = %d\n", P, nx, *S.begin());
if(op == 1)
{
node1 now = querymax(1, 1, n, P, nx);
if(*Q.begin() <= n && *Q.begin() < *S.begin() && a[*Q.begin()] > now.mx )
{
ans[++tot] = a[*Q.begin()];
P = (*Q.begin()) + 1;
Q.erase(Q.begin());
}else
{
ans[++tot] = now.mx ;
P = now.pos + 1;
S.erase(last[now.mx ]);
for(auto it = pos[now.mx ].begin(); it != pos[now.mx ].end(); ++it)
{
vis[*it] = 1;
update(1, 1, n, *it);
}
}
op ^= 1;
}else
{
node2 now = querymin(1, 1, n, P, nx);
if(*Q.begin() < *S.begin() && a[*Q.begin()] < now.mn )
{
ans[++tot] = a[*Q.begin()];
P = (*Q.begin()) + 1;
Q.erase(Q.begin());
}else
{
ans[++tot] = now.mn ;
P = now.pos + 1;
S.erase(last[now.mn ]);
for(auto it = pos[now.mn ].begin(); it != pos[now.mn ].end(); ++it)
{
vis[*it] = 1;
update(1, 1, n, *it);
}
}
op ^= 1;
}
}
printf("%d\n", m);
for(int i = 1; i <= tot; ++i) printf("%d ", ans[i]);
printf("\n");
}
return 0;
}
研讀題解，發現要維護的區間 \(\min/\max\) 的取點是一段區間，如果用 \(set\) 維護這個區間的 \(\min/\max\) ，並在全域性用 \(vis\) 陣列記錄延遲刪除，由於區間的左右端點都是遞增的，每個數只會進出 \(set\) 一次，複雜度是 \(O(n \log n)\) ，完美薄紗我的線段樹
仿照題解的2.0版本
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
int read()
{
int x = 0; bool f = false; char c = getchar();
while(c < '0' || c > '9') f |= (c == '-'), c = getchar();
while(c >= '0' && c <= '9') x = (x << 1) + (x << 3) + (c & 15), c = getchar();
return f ? -x : x;
}
const int inf = 0x3f3f3f3f;
const int N = 3e5 + 5;
int n, a[N];
int last[N], vis[N];
set<int> la;
set< pair<int, int> > mx, mn;
vector<int> ans;
int main()
{
int T = read();
while(T--)
{
n = read();
for(int i = 1; i <= n; ++i) last[i] = inf, vis[i] = 0;
la.clear(), mx.clear(), mn.clear(), ans.clear();
for(int i = 1; i <= n; ++i) a[i] = read(), last[a[i]] = i;
for(int i = 1; i <= n; ++i) la.insert(last[i]);
for(int i = 1; i <= *la.begin(); ++i)
{
mx.emplace(pair<int, int>(-a[i], i));
mn.emplace(pair<int, int>(a[i], i));
}
int pos = 0;
while(!mx.empty() || !mn.empty())
{
pair<int, int> now;
if(ans.size() & 1)
{
now = *mn.begin();
ans.emplace_back(now.first );
vis[now.first ] = 1;
}else
{
now = *mx.begin();
ans.emplace_back(-now.first );
vis[-now.first ] = 1;
}
pos = now.second + 1;
// 剔除不合法的方案，包括已經選過的數，在pos之前的數
while(*la.begin() != inf && vis[a[*la.begin()]])
{
int p = *la.begin();
la.erase(la.begin());
for(int i = p + 1; i <= min(*la.begin(), n); ++i)
{
mx.emplace(pair<int, int>(-a[i], i));
mn.emplace(pair<int, int>(a[i], i));
}
}
while(!mx.empty() && (vis[-(*mx.begin()).first ] || (*mx.begin()).second < pos)) mx.erase(mx.begin());
while(!mn.empty() && (vis[(*mn.begin()).first ] || (*mn.begin()).second < pos)) mn.erase(mn.begin());
}
printf("%d\n", ans.size());
for(int it : ans) printf("%d ", it);
printf("\n");
}
return 0;
}
總結
-
延遲刪除操作搭配 \(set\)
-
\(emplace\) 是 \(insert\) ，\(emplace\_back\) 是 \(push\_back\)
-
優先觀察要維護的資訊的單調性以及優先使用 \(STL\)
E1. Deterministic Heap (Easy Version)
沒看懂題，畫個圖理解一下，注意題中要求為滿二叉樹
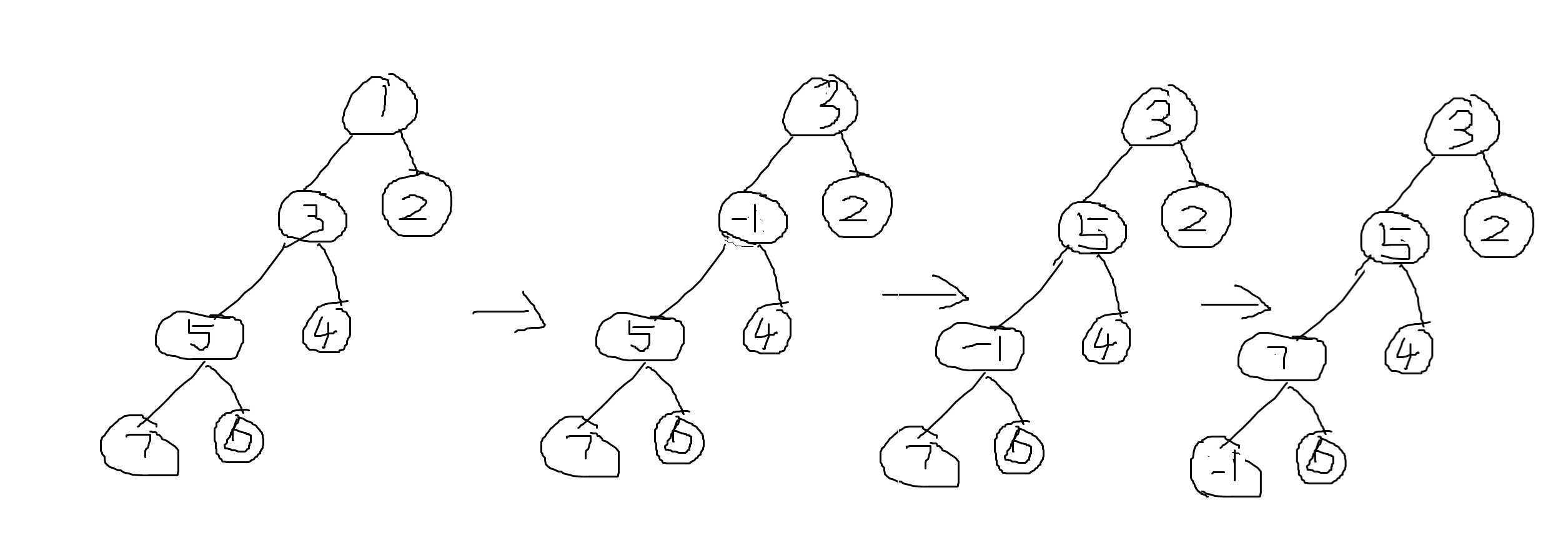
一個確定性二叉樹就是每次取較大值的兒子時選擇是唯一的，即不存在某次操作中兩個兒子的值相等的情況
如果手動模擬的話，發現這是一種遞迴操作，記錄子樹的一些必要資訊來轉化為從低向上的遞推操作
設 \(dp[i][j]\) 表示層數為 \(i\) 的二叉樹，根節點值為 \(j\) 的確定性二叉樹的個數（根節點的值即為這顆子樹進行的加操作）
發現可以只在根節點操作，即兩兒子的值的和 \(\le j\)
先求兩兒子的值的和恰好為 \(j\) 的個數，再透過字首和處理得到兩兒子的值的和 \(\le j\) 的個數
記 \(C[x][i]\) 表示在層數為 \(i\) 的二叉樹中，根節點值為 \(x\) 的個數。這是任意的二叉樹，不必滿足確定性
即在 \(2^i - 1\) 個節點中加操作 \(x\) 次，隔板法得
\[C[x][i] = \binom{x + 2^i - 2}{2^i - 2} = \binom{x + 2^i - 2}{x}
\]
\(x\) 次乘法預處理 \(C[x][i]\)
轉移時列舉左子樹根的值 \(k\) ，右子樹值為 \(j - k\) ，易得轉移：
\[dp[i][j] = \sum_{k = 0 \& k \neq j - k}^{j} dp[i - 1][\max\{k, j - k\}] \times C[\min\{k, j - k\}][i - 1]
\]
發現列舉 \(\max\{k, j - k\}\) 可以得到更優雅的公式：
\[dp[i][j] = \sum_{k = \lfloor \frac{j}{2}\rfloor + 1 }^{j} 2 \times dp[i - 1][k] \times C[j - k][i - 1]
\]
不要忘記字首和處理 \(dp[i][j]\) ！
點選檢視程式碼
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
int read()
{
int x = 0; bool f = false; char c = getchar();
while(c < '0' || c > '9') f |= (c == '-'), c = getchar();
while(c >= '0' && c <= '9') x = (x << 1) + (x << 3) + (c & 15), c = getchar();
return f ? -x : x;
}
const int N = 505;
int n, K;
ll mod;
ll jc[N], inv[N];
ll C[N][N];
ll qpow(ll a, ll b, ll mod)
{
ll ans = 1;
while(b)
{
if(b & 1) ans = ans * a % mod;
b >>= 1;
a = a * a % mod;
}
return ans;
}
void init()
{
jc[1] = jc[0] = inv[1] = inv[0] = 1;
for(int i = 2; i <= 500; ++i) jc[i] = jc[i - 1] * i % mod;
inv[500] = qpow(jc[500], mod - 2, mod);
for(int i = 499; i >= 2; --i) inv[i] = inv[i + 1] * (i + 1) % mod;
}
void getC(int x, int i)
{
ll ans = inv[x], tmp = (qpow(2, i - 1, mod) - 2 + mod) % mod;
for(int i = 1; i <= x; ++i) ans = ans * (tmp + i) % mod;
C[x][i] = ans;
}
ll dp[N][N], pd[N][N];
void add(ll &a, ll b){ a = (a + b >= mod) ? (a + b - mod) : (a + b); }
int main()
{
int T = read();
while(T--)
{
n = read(), K = read(), mod = read();
init();
for(int x = 0; x <= K; ++x)
for(int i = 2; i <= n; ++i)
getC(x, i);
for(int j = 0; j <= K; ++j) dp[1][j] = 1;
for(int i = 2; i <= n; ++i)
{
for(int j = 1; j <= K; ++j)
{
dp[i][j] = pd[i][j] = 0;
for(int k = 0; k <= j; ++k)
{
if(k == j - k) continue;
add(pd[i][j], dp[i - 1][max(k, j - k)] * C[min(k, j - k)][i] % mod);
}
add(pd[i][j], pd[i][j - 1]);
add(dp[i][j], pd[i][j]);
}
}
printf("%lld\n", dp[n][K]);
}
return 0;
}
E2. Deterministic Heap (Hard Version)
本題不保證正確性！
目前該題解只存在於理論（程式碼還沒透過）
本題的限制在於，不止第一個要求確定性，第二步也要求確定性，而第一步會改變樹的結構！
考慮如下情況：\(j > p, k > q\)
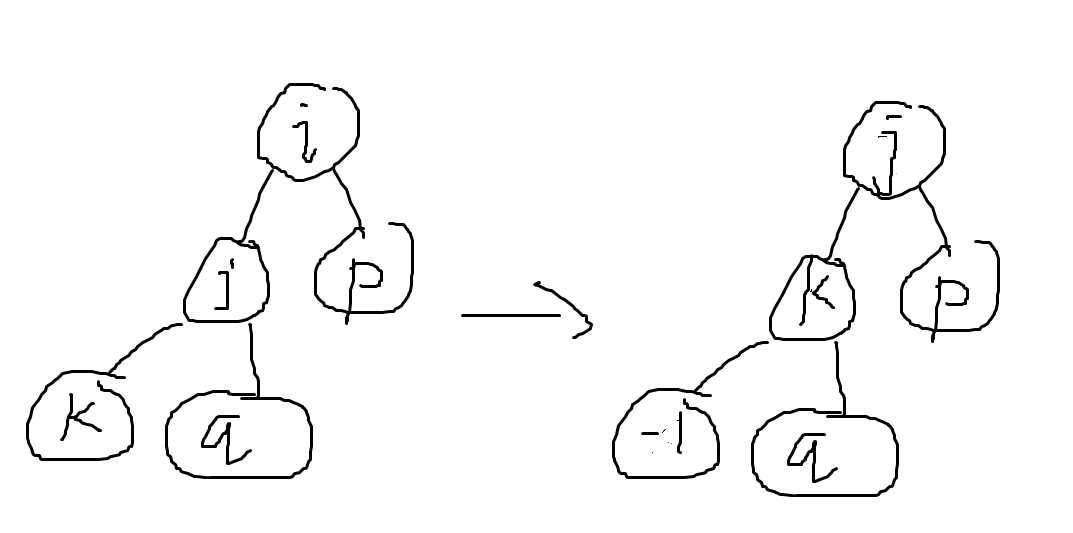
第二步則需要比較 \(k\) 與 \(p\) 的大小，用到了 \(i\) 的孫子資訊，考慮給 \(dp\) 加一維記錄兒子資訊
設 \(dp1[i][j][k]\) 表示層數為 \(i\) ，根節點值為 \(j\) ，較大兒子的值為 \(k\) 的雙步確定二叉樹個數
仍然是先求兩兒子值恰好為 \(j\) 時的個數，再字首和處理
轉移時列舉大兒子的大兒子的值 \(l\)
若 \(l > j - k\) 則相當於第二步仍選大兒子，另一棵樹隨意
\[dp1[i][j][k] = \sum_{l = j - k + 1}^{k} 2 \times dp1[i - 1][k][l] \times C[j - k][i - 1]
\]
若 \(\lfloor \frac{k}{2} \rfloor + 1 \le l < j - k\) ，需要限制大孫子的值
設 \(dp0[i][j][k]\) 表示層數為 \(i\) ，根節點值為 \(k\) ，大兒子的值為 \(k\) 的單步確定二叉樹個數
\[dp1[i][j][k] = \sum_{l = \lfloor \frac{k}{2} \rfloor + 1}^{j - k - 1} 2\times dp0[i - 1][k][l] \times dp[i - 1][j - k]
\]
對於 \(dp0\) ，仍然先求兩兒子值恰好為 \(j\) 的個數
\[dp0[i][j][k] = dp[i - 1][k] \times C[j - k][i - 1]
\]
尚未透過的程式碼
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
int read()
{
int x = 0; bool f = false; char c = getchar();
while(c < '0' || c > '9') f |= (c == '-'), c = getchar();
while(c >= '0' && c <= '9') x = (x << 1) + (x << 3) + (c & 15), c = getchar();
return f ? -x : x;
}
const int N = 505;
ll n, K, mod;
ll jc[N], inv[N];
ll qpow(ll a, ll b, ll mod)
{
ll ans = 1;
while(b)
{
if(b & 1) ans = ans * a % mod;
b >>= 1;
a = a * a % mod;
}
return ans;
}
void init()
{
jc[0] = jc[1] = inv[0] = inv[1] = 1;
for(int i = 2; i <= 500; ++i) jc[i] = jc[i - 1] * i % mod;
inv[500] = qpow(jc[500], mod - 2, mod);
for(int i = 499; i >= 2; --i) inv[i] = inv[i + 1] * (i + 1) % mod;
}
ll C[N][N]; // C(x, i)
void getC(int x, int i)
{
ll ans = inv[x], tmp = (qpow(2, i, mod) - 2 + mod) % mod;
for(int j = 1; j <= x; ++j) ans = ans * (tmp + j) % mod;
C[x][i] = ans;
}
ll dp[105][N];
ll dp0[105][N][N], dp1[105][N][N];
ll add(ll a, ll b){ return (a + b >= mod) ? (a + b - mod) : (a + b); }
int main()
{
int T = read();
while(T--)
{
n = read(), K = read(), mod = read();
init();
for(int x = 0; x <= K; ++x)
for(int i = 1; i <= n; ++i)
getC(x, i);
for(int i = 0; i <= n; ++i)
for(int j = 0; j <= K; ++j)
for(int k = 0; k <= K; ++k)
{
dp[i][j] = 0;
dp0[i][j][k] = dp1[i][j][k] = 0;
}
for(int i = 0; i <= K; ++i) dp[1][i] = 1;
for(int j = 1; j <= K; ++j)
for(int k = 1; k <= j; ++k)
dp0[2][j][k] = dp1[2][j][k] = 2 * min(k, j - k + 1);
for(int j = 1; j <= K; ++j)
for(int k = 1; k <= j; ++k)
{
dp0[2][j][k] = add(dp0[2][j][k], dp0[2][j][k - 1]);
dp1[2][j][k] = add(dp1[2][j][k], dp1[2][j][k - 1]);
}
for(int i = 2; i <= n; ++i)
for(int j = 1; j <= K; ++j)
{
// 更新 dp, pd
for(int k = (j >> 1) + 1; k <= j; ++k)
dp[i][j] = add(dp[i][j], 2ll * dp[i - 1][k] * C[j - k][i - 1] % mod);
dp[i][j] = add(dp[i][j], dp[i][j - 1]);
}
for(int i = 3; i <= n; ++i)
{
for(int j = 1; j <= K; ++j)
{
// 更新 dp0
for(int k = (j >> 1) + 1; k <= j; ++k)
dp0[i][j][k] = add(dp0[i][j][k], 2ll * dp[i - 1][k] * C[j - k][i - 1] % mod);
for(int k = 0; k <= j; ++k)
dp0[i][j][k] = add(dp0[i][j][k], dp0[i][j - 1][k]);
for(int k = (j >> 1) + 1; k <= j; ++k)
{
int l = (k >> 1) + 1, r = k;
r = min(r, j - k - 1);
if(l <= r) dp1[i][j][k] = add(dp1[i][j][k], 2ll * (dp0[i - 1][k][r] - dp0[i - 1][k][l - 1] + mod) % mod * dp[i - 1][j - k] % mod);
l = j - k + 1, r = k;
if(l <= r) dp1[i][j][k] = add(dp1[i][j][k], 2ll * (dp1[i - 1][k][r] - dp1[i - 1][k][l - 1] + mod) % mod * C[j - k][i - 1] % mod);
}
for(int k = 0; k <= j; ++k) dp1[i][j][k] = add(dp1[i][j][k], dp1[i][j - 1][k]);
}
for(int j = 1; j <= K; ++j)
for(int k = 1; k <= j; ++k)
{
dp0[i][j][k] = add(dp0[i][j][k], dp0[i][j][k - 1]);
dp1[i][j][k] = add(dp1[i][j][k], dp1[i][j][k - 1]);
}
}
// printf("%lld ", dp[n][K]);
ll ans = dp1[n][K][K];
printf("%lld\n", ans);
}
return 0;
}
/*
6
2 1 998244353
3 2 998244853
3 3 998244353
3 4 100000037
4 2 100000039
4 3 100000037
2
12
40
100
32
224
1
100 500 100000037
66681128
2
87 63 100000037
13 437 100000039
83566569
54517140
*/