Noip 複習

資料結構

ST 表

利用倍增思想，可以做到 \(O(n\log)\) 預處理 \(O(1)\) 查詢，如詢問區間最大值、最小值等

詳見 ST表詳解(稀疏表)

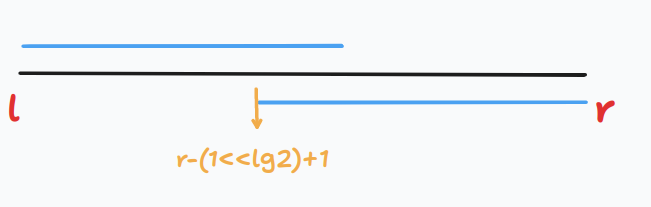
查詢大致原理如圖：

藍線長度為 \(2^{\lfloor log_2(r-l+1)\rfloor}\)，顯然大於 \(\frac{(r-l+1)}2\)，所以這兩條藍線可以做到覆蓋整個區間

倍增預處理：

for(int j=1; j<=18; j++){
    for(int i=1; i<=n; i++)
    stmax[j][i] = max(stmax[j-1][i], stmax[j-1][i+(1<<j-1)]),
    stmin[j][i] = min(stmin[j-1][i], stmin[j-1][i+(1<<j-1)]);
}

查詢：

inline int getmax(int l, int r){
    int lg2 = log2(r-l+1);
    return max(stmax[lg2][l], stmax[lg2][r-(1<<lg2)+1]);
}
inline int getmin(int l, int r){
    int lg2 = log2(r-l+1);
    return min(stmin[lg2][l], stmin[lg2][r-(1<<lg2)+1]);
}

題：

abc352D Permutation Subsequence

題解

——寫於 11.7

STL

pbds

比 STL 還 STL ！

也叫做平板電視 Here，內含比 map 快很多的雜湊表，甚至平衡樹？！

封裝了 hash、tree、trie、priority_queue 這四種資料結構

需要萬能擴充庫標頭檔案 #include<bits/extc++.h>

以及 using namespace __gnu_pbds;

內帶雜湊表：如：gp_hash_table<int, int>、cc_hash_table<int, int>

——寫於 11.7

字串演算法

manacher

馬拉車演算法（ ，OI-Wiki

演算法介紹： 線性複雜度內找出以每個字元為迴文中心的最長迴文半徑

存下模板程式碼（只用於求奇數迴文）：

int l = 0, r = -1;
for(int i=1; i<=n; i++){
    int k = i > r ? 1 : min(d[l+r-i], r-i+1);
    while(i - k > 0 and k + i <= n and s[i-k] == s[i+k]) k++;
    d[i] = k--;
    if(r < i + k) l = i - k , r = i + k;
}

偶數迴文：直接把原字串每相鄰兩個字元之間加上一個特殊字元就避免了偶數迴文的情況，如 #

當時自己推的板子是個什麼構思？？

板子題： 【模板】manacher

code

#include<bits/stdc++.h>
#define Aqrfre(x, y) freopen(#x ".in", "r", stdin),freopen(#y ".out", "w", stdout)
#define mp make_pair
#define Type ll
#define qr(x) x=read()
typedef __int128 INT;
typedef long long ll;
using namespace std;

inline ll read(){
    char c=getchar(); ll x=0, f=1;
    while(!isdigit(c)) (c=='-'?f=-1:f=1), c=getchar();
    while(isdigit(c)) x=(x<<1)+(x<<3)+(c^48), c=getchar();
    return x*f;
}

const int N = 2.2e7 + 10; 

int n, d[N];
char in[N], s[N];

signed main(){ // a
    // Aqrfre(a, a);

    cin>>(in+1); n = strlen(in+1);

    int cnt = 0;
    for(int i=1; i<=n; i++)
        s[++cnt] = '@', s[++cnt] = in[i];
    s[++cnt] = '@'; n = cnt;

    int l = 0, r = -1, ans = 0;
    for(int i=1; i<=n; i++){
        int k = i > r ? 1 : min(d[l+r-i], r-i+1);
        while(i - k > 0 and k + i <= n and s[i-k] == s[i+k]) k++;
        d[i] = k--;
        if(r < i + k) l = i - k , r = i + k;
    }

    for(int i=1; i<=n; i++){
        if(s[i] == '@') ans = max(ans, d[i] / 2 * 2); 
        else ans = max(ans, d[i] - !(d[i] & 1));
    }
    cout<<ans<<"\n";

    

    return 0;
}

最小表示法

用於解決： 有一個字串，這個字串的首尾是連在一起的，要求尋找一個位置，以該位置為起點的字串的字典序在所有的字串中中最小。

CSDN OI-Wiki

考慮在 外層列舉起點 內層遍歷以該起點打頭的字串 的基礎上進行最佳化。如果兩個字串分別是從 \(i\) 位置和 \(j\) 位置打頭的，並且有 \(s_{[i,i+k)}=s_{[j,j+k)}\)，而 \(s_{i+k}\neq s_{j+k}\)，那麼若 \(s_{i+k}>s_{j+k}\)，則顯然的有 \([i,i+k)\) 位置上的字元都不可以作為要找的位置；否則也同理。那麼這樣我們內層遍歷了多大的長度，下一次外層列舉的時候就可以忽略這麼多的長度，保證時間複雜度為 \(O(n)\) 的。

解釋一下為什麼 k==n 的時候 break，發現這種情況整個字串是會存在迴圈節的，並且以迴圈節的每一個字元為開頭都做過一遍了

模板程式碼：

int k = 0, i = 1, j = 2;
while(i <= n and j <= n){
    for(k=0; k<n; k++)
        if(in[i+k] != in[j+k]) break;
    if(k == n) break;
    if(in[i+k] < in[j+k]) j = max(j+k+1, i+1); //此時從 i~i+k 為開始的字串都會小於相應的 j~j+k 位置開始的字串，所以一定不以 j~j+k 為起點
    else i = max(i+k+1, j+1);
}i = min(i, j);

題：

Strange string

注意：輸入字元的範圍為 #33~#256，需要開 unsigned char，char 的範圍在為 -128 ~ +127

KMP

利用字尾函式線性求一個模板串在一個文字串裡出現的次數或位置等等

CSDN

預處理出模板串的最大相等前字尾，與文字串進行匹配的時候每次匹配不上就將模板串的調到與此時字尾相同的字首位置

預處理程式碼

inline void prefix(string s, int pi[]){ // pi[i]表示 s 到第 i 個字元時的串的前字尾的長度
    int len = s.length();
    for(int i=1; i<len; i++){
        int j = pi[i-1]; // j 表示到 i 前一個字元時的字首最後一個字元的位置 + 1
        while(j and s[i] != s[j]) j = pi[j-1]; //j 繼續往前跳到字首最後一個字元 + 1 的位置
        if(s[i] == s[j]) ++j; //找到最大的 j 前字尾匹配上了，長度為位置 + 1
        pi[i] = j;
    }
}   

模板題

code

#include<bits/stdc++.h>
#define Aqrfre(x, y) freopen(#x ".in", "r", stdin),freopen(#y ".out", "w", stdout)
#define mp make_pair
#define Type int
#define qr(x) x=read()
typedef long long ll;
using namespace std;

inline Type read(){
    char c=getchar(); Type x=0, f=1;
    while(!isdigit(c)) (c=='-'?f=-1:f=1), c=getchar();
    while(isdigit(c)) x=(x<<1)+(x<<3)+(c^48), c=getchar();
    return x*f;
}

const int N = 1e6 + 5; 

string s, t;
int n, m, pre[N];

inline void prefix(string s, int pi[]){ 
    int len = s.length();
    for(int i=1; i<len; i++){
        int j = pi[i-1]; 
        while(j and s[i] != s[j]) j = pi[j-1]; 
        if(s[i] == s[j]) ++j;
        pi[i] = j;
    }
}   

signed main(){ // a
    // Aqrfre(a, a);

    cin>>s>>t;
    n = s.length(), m = t.length();
    prefix(t, pre);

    for(int i=0,j=0; i<n; i++){
        while(j > 0 and s[i] != t[j]) j = pre[j-1];
        if(s[i] == t[j]) ++j;
        if(j == m){
            cout<<i-m+2<<"\n";
            j = pre[j-1];
        }
    }
    for(int i=0; i<m; i++) cout<<pre[i]<<" ";


    return 0;
}

AC 自動機

給定一個文字串和多個模式串，求出每個模式串在文字串中出現的次數，時間複雜度為所有模式串的長度和

為 trie 樹 和 KMP 的思想結合

部落格園 hyfhaha 的詳細講解

主要的三步：

1. trie 樹正常建，不再敘述

2. 構建 fail 指標：

   fail 的實質含義： 如果一個點 \(i\) 的 fail 指標指向 \(j\)，那麼 \(root\) 到 \(j\) 的字串是 \(root\) 到 \(i\) 的字串的可以在 trie 樹中找到的最長的字尾。

   在處理 \(i\) 節點時保證處理好了其父親節點 \(fa\)，（所以使用 bfs），設 \(fa->i\) 的字元為 \(c\)，這時 \(fail_i\) 指向 \(fail_{fa}\ 'son_c\)。具體操作以及細節看連結中講解

3. 查詢：

   在 trie 樹上跑文字串，每次到一個節點 \(i\)，不斷向上跳 fail 指標到根節點，即為把【 $\forall j\in $ ( \(root\) 到 \(i\) 路徑上的字元 ) 模板串 \(j\) -> \(i\) 】的貢獻加上。

   如最基礎的求每個模式串是否在文字串中出現過：對於 trie 樹上的每一個節點打個標記 \(tag\)，記以這個點結束的字串的個數，查詢的時候經過這個點一次就標記 \(tag=-1\)，保證每個點只走一次。如下文例題中的 【模板 1】

   但如果我們要求的是每個模板串在文字串中出現了幾次，顯然就不能用上述的 -1 標記最佳化了，必須每次不斷跳 fail 指標直到根節點，時間複雜度也明顯不對了，所以考慮拓撲最佳化。

   每次遇到一個節點不斷跳 fail 指標會存在以下問題：
   若有 fail 指標如下：9->7->4->2->1，並且我們跑文字串時走了 1-2-4-7-9 的路徑，每次到一個節點都會再跳 fail 指標到 1 號點。

   而又容易發現 9 的貢獻都會全加到 7 的貢獻上，同樣 7 的貢獻都會全加到 4 的貢獻上······所以我們每次遇到一個點，只更新該點的貢獻，先不往回跳 fail，最後“從深到淺”處理完 9 的所有貢獻，再去處理 7 的貢獻，這樣可以保證每個點只處理一次，複雜度是對的，本質上也就是一次拓撲的過程。

   相當於把 fail 指標看成是一條單向邊，且每個點的出度為 1，以拓撲圖的方式從深到淺更新點對應的答案。

注意題目是否存在多個模板串長得一樣，若有這種情況，還需要開個 map 記一下每種字串在 trie 樹上最後一個節點的編號

整個 trie 樹函式程式碼：

gp_hash_table<string, int>ma; //pbds 雜湊表
struct Trie{
    int rt = 1, t[M][28], fail[M<<5], in[M<<5];

    inline void insert(string s, int th){
        int len = s.length(), u = 1;
        for(int i=0; i<len; i++){
            int v = s[i] - 'a';
            if(!t[u][v]) t[u][v] = ++rt;
            u = t[u][v];
        }
        ma[s] = u; // 記字串 s 對應的節點
    }

    inline void getfail(){
        for(int i=0; i<26; i++) t[0][i] = 1;
        fail[1] = 0; q.push(1);

        while(q.size()){
            int u = q.front(); q.pop();
            for(int i=0; i<26; i++){
                int v = t[u][i];
                if(!v){ t[u][i] = t[fail[u]][i]; continue; }
                fail[v] = t[fail[u]][i];
                in[fail[v]]++; q.push(v);
            }
        }
    }

    inline void update(string s){
        int u = 1, len = s.length();
        for(int i=0; i<len; i++){
            int v = s[i] - 'a';
            u = t[u][v]; cnt[u]++;
        }
    }

    inline void topu(){
        for(int i=1; i<=rt; i++)
            if(!in[i]) q.push(i);
        while(q.size()){
            int u = q.front(); q.pop();
            int v = fail[u];
            cnt[v] += cnt[u]; in[v]--;
            if(!in[v]) q.push(v);
        }   
    }
}tri;

題

【模板 1】：求有多少個不同的模式串在文字串裡出現過。
code

【模板】AC 自動機：求每個模板串在文字串中出現的次數。code

—— AC 自動機寫於 11.8