近期，清華大學和哈爾濱工業大學聯合釋出了一篇論文：把大模型壓縮到 1.0073 個位元時，仍然能使其保持約 83% 的效能！
自從大模型火爆出圈以後，人們對壓縮大模型的願望從未消減。這是因為，雖然大模型在很多方面表現出優秀的能力，但高昂的的部署代價極大提升了它的使用門檻。這種代價主要來自於空間佔用和計算量。「模型量化」 透過把大模型的引數轉化為低位寬的表示，進而節省空間佔用。目前，主流方法可以在幾乎不損失模型效能的情況下把已有模型壓縮至 4bit。然而，低於 3bit 的量化像一堵不可逾越的高牆，讓研究人員望而生畏。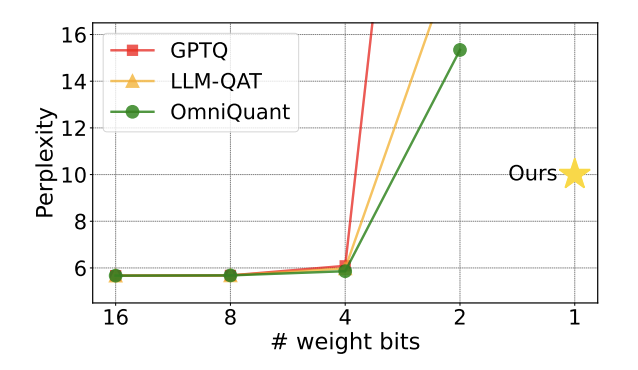
圖 1 : 量化模型的困惑度在 2bit 時迅速上升
近期，一篇由清華大學、哈爾濱工業大學合作發表在 arXiv 上的論文為突破這一阻礙帶來了希望，在國內外學術圈引起了不小的關注。這篇論文也在一週前登上 huggingface 的熱點論文，並被著名論文推薦師 AK 推薦。研究團隊直接越過 2bit 這一量化級別，大膽地進行了 1bit 量化的嘗試，這在模型量化的研究中尚屬首次。
論文標題：OneBit: Towards Extremely Low-bit Large Language Models論文地址：https://arxiv.org/pdf/2402.11295.pdf作者提出的方法稱作 「OneBit」，非常貼切地形容了這一工作的本質：把預訓練大模型壓縮到真正的 1bit。該論文提出了模型引數 1bit 表示的新方法，以及量化模型引數的初始化方法，並透過量化感知訓練（QAT）把高精度預訓練模型的能力遷移至 1bit 量化模型。實驗表明，這一方法能夠在極大幅度壓縮模型引數的同時，保證 LLaMA 模型至少 83% 的效能。作者指出，當模型引數壓縮至 1bit 後，矩陣乘法中的 「元素乘」將不復存在，取而代之的是更快速的 「位賦值」操作，這將大大提升計算效率。這一研究的重要意義在於，它不但跨越了 2bit 量化的鴻溝，也使在 PC 和智慧手機上部署大模型成為可能。模型量化主要透過把模型的 nn.Linear 層（Embedding 層和 Lm_head 層除外）轉化為低精度表示實現空間壓縮。此前工作 [1,2] 的基礎是利用 Round-To-Nearest（RTN）方法把高精度浮點數近似對映到附近的整數網格。這可以被表示成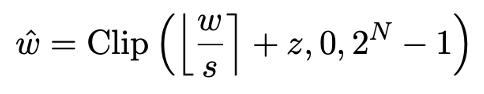
。然而基於 RTN 的方法在極低位寬時（3bit 以下）存在嚴重的精度損失問題，量化後的模型能力損失十分嚴重。特別是，量化後引數以 1bit 表示時，RTN 中的縮放係數 s 和零點 z 會失去實際意義。這導致基於 RTN 的量化方法在 1bit 量化時幾乎失效，難以有效地保留原模型的效能。此外，此前的研究中也曾對 1bit 模型可能採用什麼結構進行過探索。幾個月前的工作 BitNet [3] 透過讓模型引數透過 Sign (・) 函式並轉為 + 1/-1 來實現 1bit 表示。但這一方法存在效能損失嚴重、訓練過程不穩定的問題，限制了其實際應用。OneBit 的方法框架包括全新的 1bit 層結構、基於 SVID 的引數初始化方法和基於量化感知知識蒸餾的知識遷移。OneBit 的終極目標是將 LLMs 的權重矩陣壓縮到 1bit。真正的 1bit 要求每個權重值只能用 1bit 表示，即只有兩種可能的狀態。作者認為，在大模型的引數中，有兩個重要因素都必須被考慮進來，那就是浮點數的高精度和引數矩陣的高秩。因此，作者引入兩個 FP16 格式的值向量以補償由於量化導致的精度損失。這種設計不僅保持了原始權重矩陣的高秩，而且透過值向量提供了必要的浮點精度，有助於模型的訓練和知識遷移。1bit 線性層的結構與 FP16 高精度線性層的結構對比如下圖： 圖 3 : FP16 線性層與 OneBit 線性層的對比左側的 (a) 是 FP16 精度模型結構，右側的 (b) 是 OneBit 框架的線性層。可見，在 OneBit 框架中，只有值向量 g 和 h 保持 FP16 格式，而權重矩陣則全部由 ±1 組成。這樣的結構兼顧了精度和秩，對保證穩定且高質量的學習過程很有意義。OneBit 對模型的壓縮幅度究竟如何？作者在論文中給了一個計算。假設對一個 4096*4096 的線性層進行壓縮，那麼 OneBit 需要一個 4096*4096 的 1bit 矩陣，和兩個 4096*1 的 16bit 值向量。這裡面總的位數為 16,908,288，總的引數個數為 16,785,408，平均每個引數佔用僅僅約 1.0073 個 bit。這樣的壓縮幅度是空前的，可以說是真正的 1bit 大模型。為了使用充分訓練好的原模型更好地初始化量化後的模型，進而促進更好的知識遷移效果，作者提出一種新的引數矩陣分解方法，稱為 「值 - 符號獨立的矩陣分解（SVID）」。這一矩陣分解方法把符號和絕對值分開，並把絕對值進行秩 - 1 近似，其逼近原矩陣引數的方式可以表示成：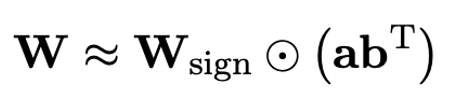
這裡的秩 - 1 近似可以透過常見的矩陣分解方式實現，例如奇異值分解（SVD）和非負矩陣分解（NMF）。而後，作者在數學上給出這種 SVID 方法可以透過交換運算次序來和 1bit 模型框架相匹配，進而實現引數初始化。並且，論文還證明了符號矩陣在分解過程中確實起到了近似原矩陣的作用。作者指出，解決大模型超低位寬量化的有效途徑可能是量化感知訓練 QAT。在 OneBit 模型結構下，透過知識蒸餾從未量化模型中學習，實現能力向量化模型的遷移。具體地，學生模型主要接受教師模型 logits 和 hidden state 的指導。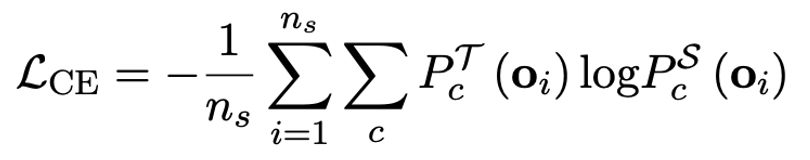
訓練時，值向量和矩陣的值會被更新。模型量化完成後，直接把 Sign (・) 後的引數儲存下來，在推理和部署時直接使用。OneBit 與 FP16 Transformer、經典的訓練後量化強基線 GPTQ、量化感知訓練強基線 LLM-QAT 和最新的 2bit 權重量化強基線 OmniQuant 進行了比較。此外，由於目前還沒有 1bit 權重量化的研究，作者只對自己的 OneBit 框架使用了 1bit 權重量化，而對其他方法採取 2bit 量化設定，屬於典型的 「以弱勝強」。在模型選擇上，作者也選擇了從 1.3B 到 13B 不同大小、OPT 和 LLaMA-1/2 不同系列的模型來證明 OneBit 的有效性。在評價指標上，作者沿用了以往模型量化的兩大評價維度：驗證集的困惑度和常識推理的 Zero-shot 準確度。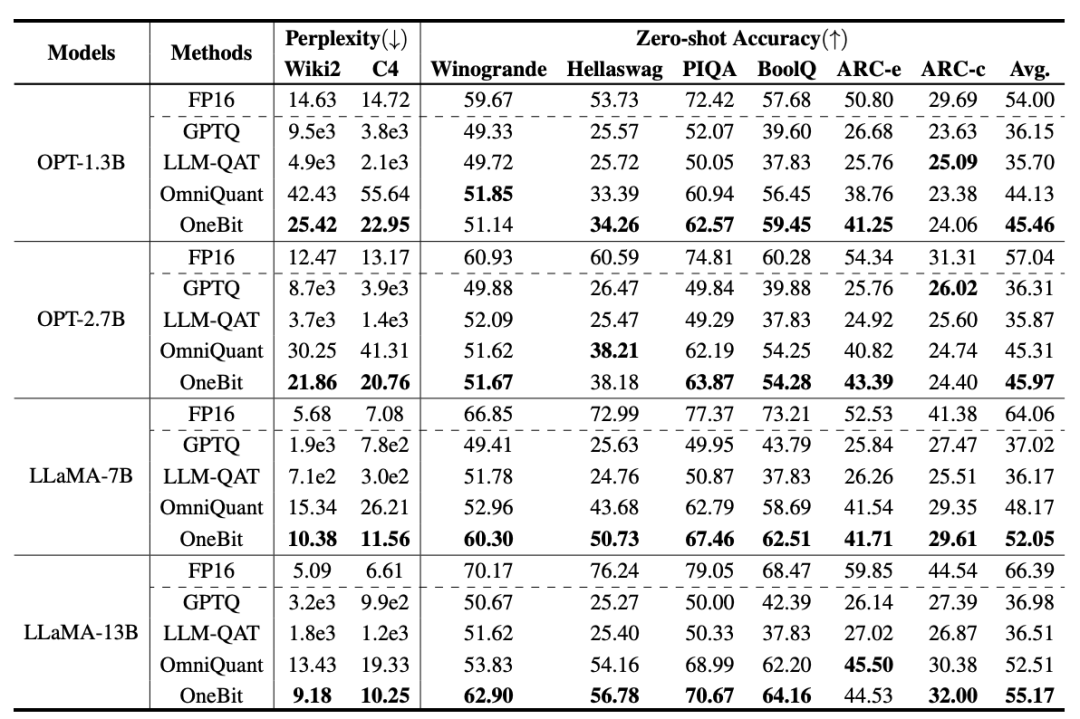
表 1 : OneBit 與基線方法的效果比較（OPT 模型與 LLaMA-1 模型）
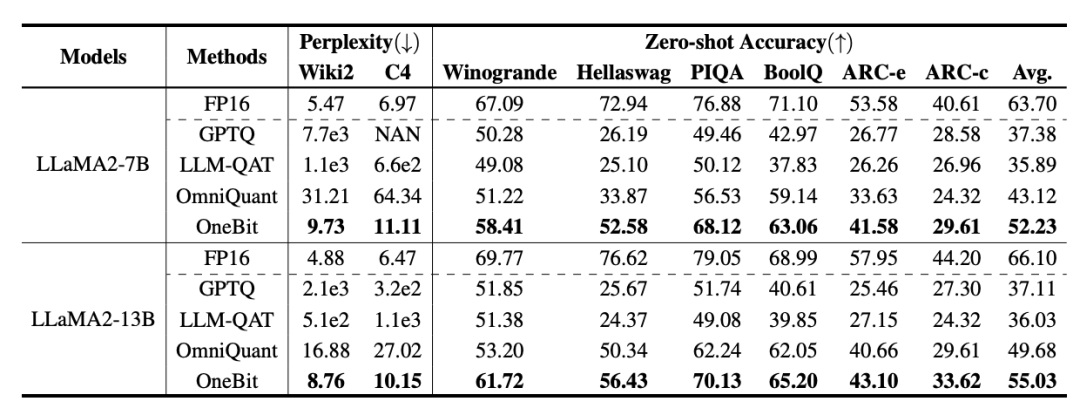
表 2 : OneBit 與基線方法的效果比較（LLaMA-2 模型）表 1 和表 2 展示出了 OneBit 相比於其他方法在 1bit 量化時的優勢。就量化模型在驗證集的困惑度而言，OneBit 與 FP16 模型最為接近。就 Zero-shot 準確度而言，除 OPT 模型的個別資料集外，OneBit 量化模型幾乎取得了最佳的效能。其餘的 2bit 量化方法在兩種評價指標上呈現較大的損失。值得注意的是，OneBit 在模型越大時，效果往往越好。也就是說，隨著模型規模增大，FP16 精度模型在困惑度降低上收效甚微，但 OneBit 卻表現出更多的困惑度下降。此外，作者還指出量化感知訓練對於超低位寬量化或許十分有必要。
圖 4 : 常識推理任務對比
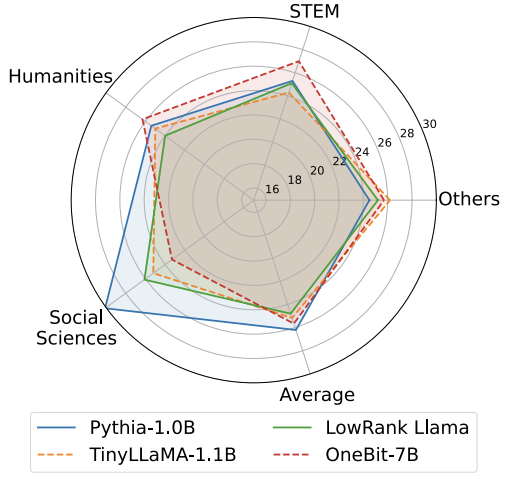
圖 4 - 圖 6 還對比了幾類小模型的空間佔用和效能損失，它們是透過不同的途徑獲得的：包括兩個充分訓練的模型 Pythia-1.0B 和 TinyLLaMA-1.1B，以及透過低秩分解獲得的 LowRank Llama 和 OneBit-7B。可以看出，儘管 OneBit-7B 有最小的平均位寬、佔用最小的空間，它在常識推理能力上仍然優於不遜於其他模型。作者同時指出，模型在社會科學領域面臨較嚴重的知識遺忘。總的來說，OneBit-7B 展示出了其實際應用價值。正如圖 7 所展示的，OneBit 量化後的 LLaMA-7B 模型經過指令微調後，展示出了流暢的文字生成能力。
圖 7 : OneBit 框架量化後的 LLaMA-7B 模型的能力
表 3 : OneBit 在不同 LLaMA 模型的壓縮比
表 3 給出的是 OneBit 對不同規模 LLaMA 模型的壓縮比。可以看出，OneBit 對模型的壓縮比均超過 90%，這一壓縮能力是史無前例的。其中值得注意的是，隨著模型增大，OneBit 的壓縮比越高，這是由於 Embedding 層這種不參與量化的引數佔比越來越小。前文提到，模型越大，OneBit 帶來的效能增益越大，這顯示出 OneBit 在更大模型上的優勢。
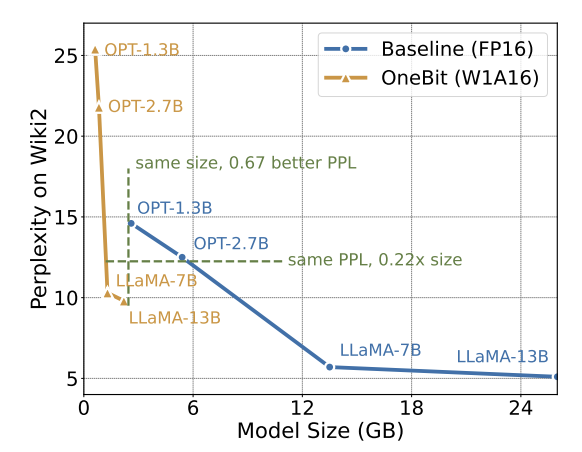
雖然超低位元量化可能會導致一定的效能損失，但如圖 8 所示，它在大小和效能之間達到了良好的平衡。作者認為，壓縮模型的大小十分重要，特別是在移動裝置上部署模型時。此外，作者還指出了 1bit 量化模型在計算上的優勢。由於引數是純二進位制的，可以用 0/1 在 1bit 內表示，這毫無疑問地節省大量的空間。高精度模型中矩陣乘法的元素相乘可以被變成高效的位運算，只需位賦值和加法就可以完成矩陣乘積，非常有應用前景。二值網路普遍面臨訓練不穩定、收斂困難的問題。得益於作者引入的高精度值向量，模型訓練的前向計算和後向計算均表現的十分穩定。BitNet 更早地提出 1bit 模型結構，但該結構很難從充分訓練的高精度模型中遷移能力。如圖 9 所示，作者嘗試了多種不同的學習率來測試 BitNet 的遷移學習能力，發現在教師指導下其收斂難度較大，也在側面證明了 OneBit 的穩定訓練價值。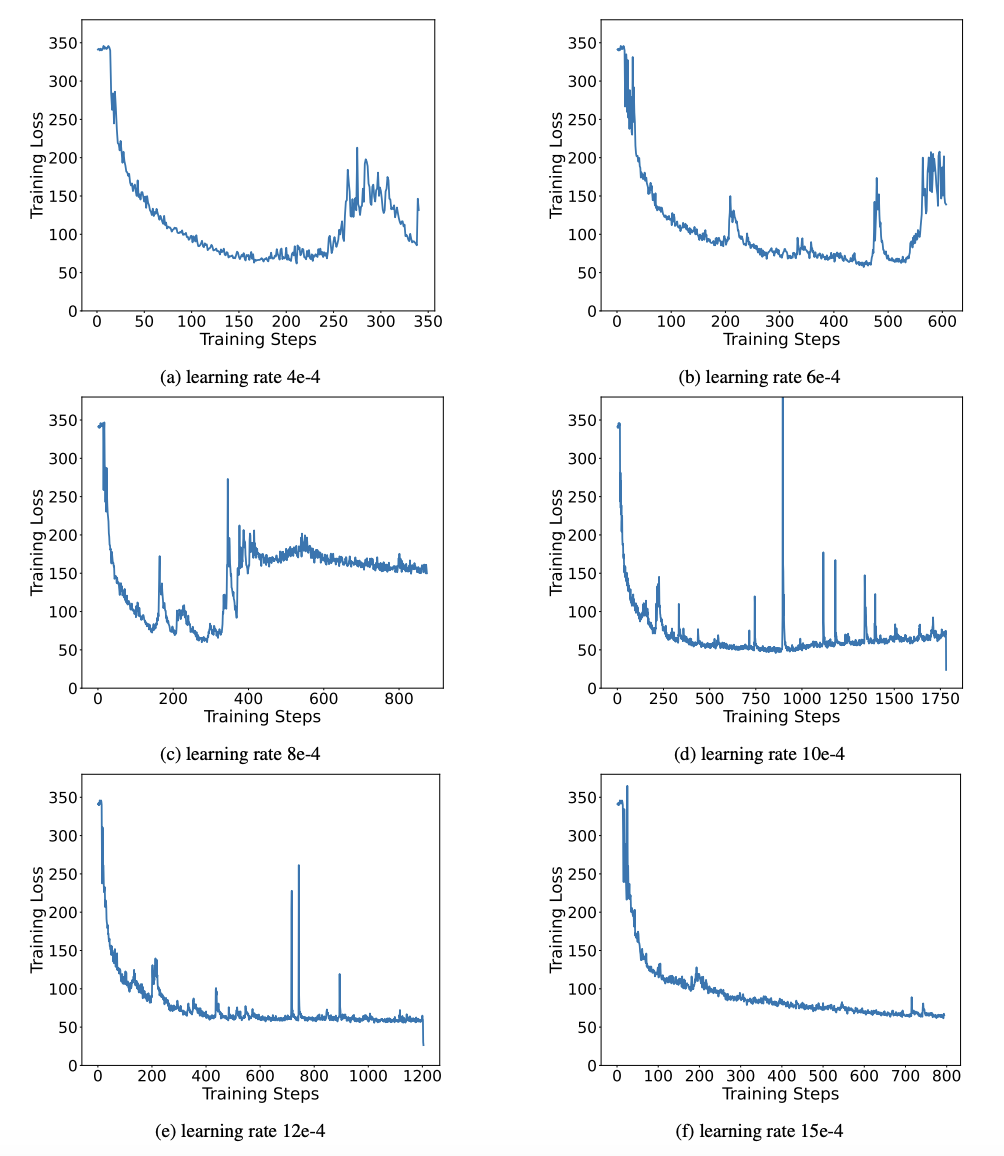
圖 9 : BitNet 在多種不同學習率下的訓練後量化能力
論文的最後，作者還建議了超低位寬未來可能得研究方向。例如，尋找更優的引數初始化方法、更少的訓練代價，或進一步考慮啟用值的量化。[1] Dettmers T, Lewis M, Belkada Y, et al. Llm. int8 (): 8-bit matrix multiplication for transformers at scale [J]. arXiv preprint arXiv:2208.07339, 2022.[2] Frantar E, Ashkboos S, Hoefler T, et al. GPTQ: Accurate post-training quantization for generative pre-trained transformers [J]. arXiv preprint arXiv:2210.17323, 2022.[3] Wang H, Ma S, Dong L, et al. Bitnet: Scaling 1-bit transformers for large language models [J]. arXiv preprint arXiv:2310.11453, 2023.