【筆記】哈夫曼樹
哈夫曼樹又稱最優二叉樹。它是一種帶權路徑長度最短的樹,應用非常廣泛。
1.哈夫曼樹的概念
- 擴充二叉樹
對每棵二叉樹進行擴充:每當在原來的二叉樹中出現空子樹時,就加上一個特殊的結點。顯然,每個內節點都有兩個兒子,而每個方結點都沒有兒子,如果二叉樹有n個內結點和S個外結點,則S=n+1,即外結點的個數比內結點的個數多1.
設已按此法將第一顆二叉樹加以擴充,樹的外路長(用E表示)定義為從根結點到外結點的路長之和,而內路長(用I表示)定義為從根結點到每個內結點的路長之和。他們總是滿足E=I+2n。
- 路徑和路徑長度
路徑是指在樹中一個結點到另一個結點所走過的路程。路徑長度是一個結點到另一個結點之間的分支數目。樹的路徑長度是指從樹根到每個結點的路徑長度的和。
- 樹的帶權路徑長度
結點的帶權路徑長度為從該結點到樹根之間的路徑長度與即誒但上權的乘積。樹的帶權路徑長度為樹中所有葉子結點的帶權路徑長度之和,通常記作
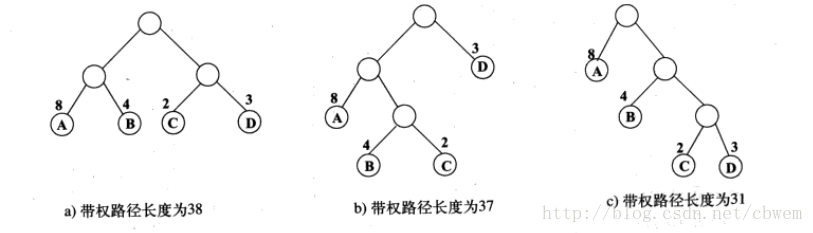
注意:加權路長最小者並非一定是完全平衡的二叉樹。
2.哈夫曼樹的構造演算法
哈夫曼樹就是帶權路徑長度最小的樹,權值最小的結點原理根結點,權值越大的結點越靠近根結點。
哈夫曼樹的構造演算法:
- 由給定的n個權值{
w1,w2,…,wn w_1,w_2,…,w_n}構成n棵只有根結點的二叉樹集合F=T1,T2,…,Tn F={T_1,T_2,…,T_n},其中每棵二叉樹Ti T_i中只有一個帶權為wi w_i的根結點,其左右子樹均為空。- 在二叉樹集合
F F中選區兩棵根結點的權值最小的和次小的的樹作為左、右子樹構造一棵新的二叉樹,新二叉樹的根結點的權重為這兩棵子樹根結點的權重之和。- 在二叉樹集合F中刪除這兩棵二叉樹,並將新得到的二叉樹加入到集合F中。
- 重複步驟2和3,指導結合F中只剩下一棵二叉樹為止。這棵樹就是最優二叉樹——哈夫曼樹。
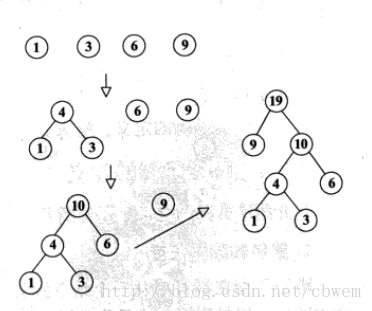
3.哈夫曼編碼
在電報的傳輸過程中,需將傳送的文字轉換成二進位制的字元組成的字串。在傳送電文時,希望電文的長度儘可能短。如果按照每個字元進行長度不等的編碼,將出現頻率高的字元采用盡可能短的編碼,則電文的程式碼長度就會減少。用一個二進位制數字串對每個字元進行編碼,使任意一個字元的編碼不會是任何其他字元編碼的字首。通常把編碼的這種特性叫做字首性,字首性使兩個字元編碼之間不需要加分隔符。可以按下述方法對二進位制數字進行譯碼:反覆刪去該串的字首,這些字首就是一些字元的編碼。因此所設計的長度不等的編碼必須滿足任意一個字元的編碼都不是另一個字元的字首的要求,這樣的編碼稱為字首編碼。
可以將字首編碼看成二叉樹中的路徑。每個結點的左分支附以一個0,而結點的右分支附以一個1,將字元作為葉結點的標號。從根結點到葉結點的路徑上遇到0或1構成的序列就是相應的字元的編碼。因此任意一種字首編碼都可以用一棵二叉樹來表示。
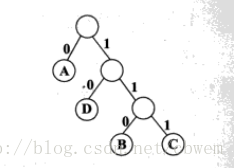
哈夫曼編碼演算法的基本思想:從給定的字符集中選擇出現概率最小的兩個字元a、b;用一個字元(如x)代替a和b,而x的概率對應於a和b的概率之和。然後,對新的、字元個數較少的字符集(去掉a、b而加上x)遞迴地求最佳字首編碼。原來的字符集中字元的編碼可以這樣得到:a的編碼是在x編碼後附以0,而b的編碼是在x的編碼後附以1。
每棵樹中葉結點的標號是要編碼的字元,其跟記載該樹所有葉結點字元所對應的概率之和,此和數稱為該樹的權。起初,每個字元本身是一棵樹;當演算法那結束時,形成唯一的一棵樹,所有的字元都在它的葉結點上。從根結點到葉結點的路徑上的0、1序列就表示該葉結點標號的編碼。對於給定的字符集和出現的概率,哈夫曼樹所表示的字元的編碼的平均長度最小。
4.哈夫曼編碼演算法的實現
假設一個字元序列為{a,b,c,d},對應的權重為{2,3,6,8}。構造一棵哈夫曼樹,然後輸出相應的哈夫曼編碼。
- 哈夫曼樹的型別定義
typedef struct
{
unsigned int weight;
unsigned int parent,lchild,rchild;
}HTNode,*HuffmanTree;
typedef char **HuffmanCode; /*存放哈夫曼編碼*/HuffmanCode為一個二級指標,相當於二維陣列,用來存放每一個葉子結點的哈夫曼編碼。起初時,將每一個葉子結點的雙親結點域、左孩子域和右孩子域都初始化為0。若有n個葉子結點,則非葉子結點有n-1個,所以總共結點數目是2n-1個。同時也要將剩下的n-1個雙親結點域初始化為0,這主要是為了查詢權值最小的結點方便。
- 建立哈夫曼樹並構造哈夫曼編碼
一次選擇兩個權值最小的結點s1和s2分別作為左子樹結點和右子樹結點,併為其雙親結點賦予一個地址,雙親結點的權值為s1和s2的權值之和。修改它們的parent域,使它們指向同一個雙親結點,雙親結點的左子樹為權值最小的結點,右子樹為權值次小的結點。重複執行這種操作n-1次,即求出n-1個非葉子結點的權值。這樣就構造出了一棵哈夫曼樹。
求哈夫曼編碼的方式有兩種,即從根結點開始到葉子結點正向求哈夫曼編碼和從葉子結點到根結點你想求哈夫曼編碼,這裡給出從根結點到葉子結點求哈夫曼編碼的演算法:
從編號為2n-1的結點開始,即根結點開始,依次通過判斷左孩子和右孩子是否存在進行編碼,若左孩子存在則編碼為0,若右孩子存在則編碼為1;同時,利用weight域作為結點是否已經訪問的標誌位,若左孩子結點已經訪問則將相應的weight域置為1,若右孩子結點也已經訪問過則將相應的weight域置為2,若左孩子和右孩子都已經訪問過則回退至雙親結點。按照這個思路,指導所有結點都已經訪問過,並回退至根結點,則演算法結束。
void HuffmanCoding(HuffmanTree *HT,HuffmanCode *HC,int *w,int n)
/*構造哈夫曼樹HT,並從根結點到葉子結點求赫夫曼編碼並儲存在HC中*/
{
int s1,s2,i,m;
unsigned int r,cdlen;
char *cd;
HuffmanTree p;
if(n<=1)
return;
m=2*n-1;
*HT=(HuffmanTree)malloc((m+1)*sizeof(HTNode));
for(p=*HT+1,i=1;i<=n;i++,p++,w++)
{
(*p).weight=*w;
(*p).parent=0;
(*p).lchild=0;
(*p).rchild=0;
}
for(;i<=m;++i,++p)
(*p).parent=0;
/*構造哈夫曼樹HT*/
for(i=n+1;i<=m;i++)
{
Select(HT,i-1,&s1,&s2);
(*HT)[s1].parent=(*HT)[s2].parent=i;
(*HT)[i].lchild=s1;
(*HT)[i].rchild=s2;
(*HT)[i].weight=(*HT)[s1].weight+(*HT)[s2].weight;
}
/*從根結點到葉子結點求赫夫曼編碼並儲存在HC中*/
*HC=(HuffmanCode)malloc((n+1)*sizeof(char*));
cd=(char*)malloc(n*sizeof(char));
r=m; /*從根結點開始*/
cdlen=0; /*編碼長度初始化為0*/
for(i=1;i<=m;i++)
(*HT)[i].weight=0; /*將weight域作為狀態標誌*/
while(r)
{
if((*HT)[r].weight==0)/*如果weight域等於零,說明左孩子結點沒有遍歷*/
{
(*HT)[r].weight=1; /*修改標誌*/
if((*HT)[r].lchild!=0) /*如果存在左孩子結點,則將編碼置為0*/
{
r=(*HT)[r].lchild;
cd[cdlen++]='0';
}
else if((*HT)[r].rchild==0) /*如果是葉子結點,則將當前求出的編碼儲存到HC中*/
{
(*HC)[r]=(char *)malloc((cdlen+1)*sizeof(char));
cd[cdlen]='\0';
strcpy((*HC)[r],cd);
}
}
else if((*HT)[r].weight==1) /*如果已經訪問過左孩子結點,則訪問右孩子結點*/
{
(*HT)[r].weight=2; /*修改標誌*/
if((*HT)[r].rchild!=0)
{
r=(*HT)[r].rchild;
cd[cdlen++]='1';
}
}
else /*如果左孩子結點和右孩子結點都已經訪問過,則退回到雙親結點*/
{
r=(*HT)[r].parent;
--cdlen; /*編碼長度減1*/
}
}
free(cd);
}- 查詢權值最小和次小的兩個結點
int Min(HuffmanTree t,int n)
/*返回樹中n個結點中權值最小的結點序號*/
{
int i,flag;
int f=infinity; /*f為一個無限大的值*/
for(i=1;i<=n;i++)
if(t[i].weight<f&&t[i].parent==0)
f=t[i].weight,flag=i;
t[flag].parent=1; /*給選中的結點的雙親結點賦值1,避免再次查詢該結點*/
return flag;
}
void Select(HuffmanTree *t,int n,int *s1,int *s2)
/*在n個結點中選擇兩個權值最小的結點序號,其中s1最小,s2次小*/
{
int x;
*s1=Min(*t,n);
*s2=Min(*t,n);
if((*t)[*s1].weight>(*t)[*s2].weight)/*若序號s1的權值大於s2的權值,將兩者交換,使s1最小,s2次小*/
{
x=*s1;
*s1=*s2;
*s2=x;
}
}
- 主函式檔案
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<malloc.h>
#define infinity 65535 /*定義一個無限大的值*/
/*哈夫曼樹型別定義*/
typedef struct
{
unsigned int weight;
unsigned int parent,lchild,rchild;
}HTNode,*HuffmanTree;
typedef char **HuffmanCode; /*存放哈夫曼編碼*/
int Min(HuffmanTree t,int n);
void Select(HuffmanTree *t,int n,int *s1,int *s2);
void HuffmanCoding(HuffmanTree *HT,HuffmanCode *HC,int *w,int n);
void main()
{
HuffmanTree HT;
HuffmanCode HC;
int *w,n,i;
printf("請輸入葉子結點的個數: ");
scanf("%d",&n);
w=(int*)malloc(n*sizeof(int)); /*為n個結點的權值分配記憶體空間*/
for(i=0;i<n;i++)
{
printf("請輸入第%d個結點的權值:",i+1);
scanf("%d",w+i);
}
HuffmanCoding(&HT,&HC,w,n);
for(i=1;i<=n;i++)
{
printf("哈夫曼編碼:");
puts(HC[i]);
}
/*釋放記憶體空間*/
for(i=1;i<=n;i++)
free(HC[i]);
free(HC);
free(HT);
}- 測試結果

在演算法的實現過程中,陣列HT在初始時和哈夫曼樹生成後的狀態如下圖所示。
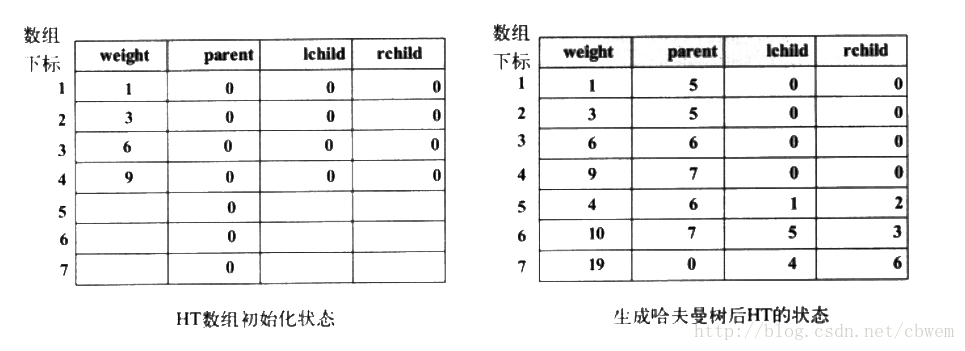
相關文章
- 哈夫曼樹學習筆記筆記
- 哈夫曼樹
- Java 樹結構實際應用 二(哈夫曼樹和哈夫曼編碼)Java
- 樹和二叉樹的基本運算實現-哈夫曼樹/哈夫曼編碼二叉樹
- 6.6 哈夫曼樹及其應用
- 資料結構與演算法——赫夫曼樹(哈夫曼樹)資料結構演算法
- 哈夫曼二叉樹原始碼 (轉)二叉樹原始碼
- 重學資料結構之哈夫曼樹資料結構
- 哈夫曼樹及其應用(檔案壓縮)
- 最優二叉樹(哈夫曼樹)Java實現二叉樹Java
- 資料結構-哈夫曼樹(python實現)資料結構Python
- 資料結構與演算法:哈夫曼樹資料結構演算法
- 【資料結構X.11】程式碼實現 哈夫曼樹的建立,建立,構造,實現哈夫曼編碼資料結構
- [java]java實現哈夫曼編碼Java
- 【資料結構】哈夫曼樹的建立與基礎應用資料結構
- POJ 3253-Fence Repair(哈夫曼樹-最小值優先佇列)AI佇列
- 高階資料結構---赫(哈)夫曼樹及java程式碼實現資料結構Java
- 哈夫曼編碼 —— Lisp 與 Python 實現LispPython
- 合併果子(優先佇列 +或者+哈夫曼)佇列
- 樹(4)--赫夫曼樹及其應用
- POJ 3253Fence Repair(哈夫曼&優先佇列)AI佇列
- php二叉樹與赫夫曼樹PHP二叉樹
- 一本正經的聊資料結構(6):最優二叉樹 —— 哈夫曼樹資料結構二叉樹
- 資料結構之哈弗曼樹資料結構
- C#資料結構-赫夫曼樹C#資料結構
- 哈夫曼實現檔案壓縮解壓縮(c語言)C語言
- 傳記《盛田昭夫》筆記筆記
- [筆記]AVL樹筆記
- 隱馬爾可夫模型 | 賽爾筆記隱馬爾可夫模型筆記
- Safe Or Unsafe(hdu2527)哈弗曼VS優先佇列佇列
- 線段樹筆記筆記
- 樹莓派筆記樹莓派筆記
- [筆記]樹形dp筆記
- 【筆記】圓方樹筆記
- *衡樹 Treap(樹堆) 學習筆記筆記
- 39.Redis總結 嘻哈的簡寫筆記——RedisRedis筆記
- 機器學習筆記--決策樹機器學習筆記
- 平衡樹學習筆記筆記