最近模擬賽抽象題太多了,讓他們聚一聚
T1 多校A層衝刺NOIP2024模擬賽18 T3 DBA
暴力比較顯然,直接數位dp就好,記搜的複雜度是\(O(n^4)\)的,用遞推加字首和最佳化可以最佳化為\(O(n^3)\),但我還是不理解\(O(n^3)\)憑啥能\(拿97pts\),雖然和正解沒啥關係,但還是放一下記搜的程式碼:
點選檢視程式碼
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=2000+5,p=1e9+7;
int n,m,a[N];
int x,y,z,l,r,k,t;
int dp[N][15000],ans,tot;
//dp[i][j]表示截止到第i位,和為j的方案數
int dfs(int pos,int sum,bool limit){
if(pos>n){
if(sum==tot)return 1;
else return 0;
}
if(sum>tot)return 0;
if(dp[pos][sum]!=-1&&(!limit))return dp[pos][sum];
int lim=limit?a[pos]:m-1,res=0;
for(int i=0;i<=lim;i++){
res+=dfs(pos+1,sum+i,limit&&i==lim);
}
dp[pos][sum]=res%p;
return res%p;
}
signed main(){
freopen("dba.in","r",stdin);
freopen("dba.out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>m>>n;
memset(dp,-1,sizeof dp);
for(int i=1;i<=n;i++)cin>>a[i],tot+=a[i];
cout<<dfs(1,0,1)-1<<endl;
return 0;
}
點選檢視程式碼
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=2000+5,p=1e9+7;
int n,m,fac[N*N],inv[N*N];
int x,y,z,l,r,k,t,sum;
int ans,tot,a[N];
inline int quickpow(int a,int b){
int res=1;
while(b){
if(b&1)res=res*a%p;
b>>=1;
a=a*a%p;
}return res;
}
void iint(){
fac[0]=1;
for(int i=1;i<=n*m;i++)fac[i]=fac[i-1]*i%p;
inv[n*m]=quickpow(fac[n*m],p-2);
for(int i=n*m-1;i>=0;i--)inv[i]=inv[i+1]*(i+1)%p;
}
inline int C(int n,int m){
if(n<m)return 0;
return fac[n]*inv[n-m]%p*inv[m]%p;
}
inline int slove(int a,int w){
int res=0;
for(int i=0,f=1;i<=a&&i*m<=sum;i++,f=-f){
res+=f*(C(sum-i*m+a,a)-C(sum-w-i*m+a,a)+p)%p*C(a,i)%p+p;
}return res%p;
}
signed main(){
freopen("dba.in","r",stdin);
freopen("dba.out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>m>>n;
iint();
for(int i=1;i<=n;i++)cin>>a[i],sum+=a[i];
for(int i=1;i<n;i++)ans+=slove(n-i,a[i]),sum-=a[i];
cout<<ans%p<<'\n';
return 0;
}
T2 多校A層衝刺NOIP2024模擬賽18 T4 銀行的源起
首先講一下\(O(n^2)\)的做法。
先考慮如果只有一個銀行,有一個比較一眼但又不太好想到的性質即為:對於每條邊將樹分為兩部分1,2,如果要想讓其最優,要麼1中的點全都透過這條邊跑到2,要麼2中的點全都透過這條邊跑到1,即對於每條邊的貢獻為\(e[i].w*min(size[x],totsize-size[x])\),這樣可以保證讓每條邊的貢獻是最優的,推廣到全域性即能保證答案最優,這樣就可以\(O(n)\)求解最小代價。
考慮兩個銀行怎麼做,如果有兩個銀行,那麼有一條邊肯定是不會被任何點經過的,那麼原圖就被分成了兩個部分,這兩個部分都只有一個銀行,可以直接\(O(n)\)求解,具體如圖:
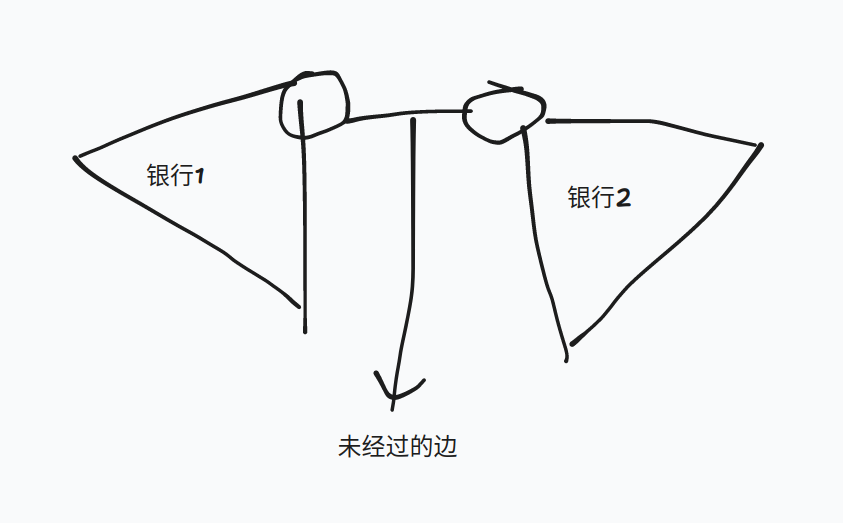
直接列舉哪條邊未被經過即可,複雜度\(O(n^2)\)
既然我講了\(O(n^2)\)做法,那正解肯定和它有點關係,考慮如果要想保證答案正確性,列舉那條邊未被經過這個過程肯定不能少,那隻能考慮去最佳化求解貢獻的過程,這個時候看這個式子是帶著\(min\)的,考慮拆開分類討論一下:
當\(size[x]>totsize/2\)時貢獻為\(e[i].w*size[x]\),反之\(size[x]<=totsize/2\)貢獻為\(totsize*e[i].w-size[x]*e[i].w\),觀察到貢獻是和\(size[x]\)緊密相關的,可以直接開一個以\(size\)為下標的權值線段樹,查詢貢獻時直接找到\(size=totsize/2\)的位置,左邊,右邊分別算貢獻即可。
考慮線段樹要維護什麼資訊,看上面的式子,分別用到了\(e[i].w,e[i].w*size[x]\),直接分別維護即可,至於線段樹資訊怎麼更新,額....,好問題,你發現如果只考慮一棵子樹內的貢獻的話,你直接線段樹合併即可,但是另一部分的答案就會變得很難統計,這個時候就不太能用這個線段樹上的資訊來計算了,所以這個時候我們就要考慮怎麼再去維護那一部分的資訊。
首先先上一個圖,便於一會描述:
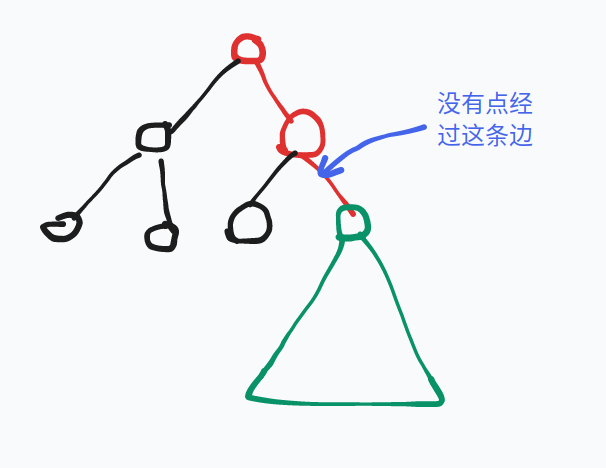
現在我們以箭頭指向的那條邊為界將樹分為了兩部分:綠色子樹和(紅+黑)的那棵樹
首先綠色子樹的貢獻直接就可以線段樹合併的時候計算,沒啥要說的
主要還是紅黑部分的貢獻的計算:
首先這紅黑兩部分的\(size_{紅黑}=totsize-size_{綠色子樹}\)
先考慮紅色這條鏈的貢獻計算,可以發現紅色這條鏈完全可以用一個權值樹狀陣列,當你進入一個節點時加上它的貢獻,離開時再減去就好,貢獻的計算和上面一樣,只不過它這條鏈上的每一個節點的\(size\)都減去了一個\(size_{綠色子樹}\),查詢時分界點稍微左偏一下即可
再考慮黑色部分的貢獻,雖說它的\(size\)並沒有發生改變,但你發現它根本沒法用任何東西維護,這個時候就可以直接統計全域性對於\(size_{紅黑}\)的貢獻,然後直接減去綠色子樹和紅色鏈上對於\(size_{紅黑}\)的貢獻就好了,這兩個東西都是可以\(O(log)\)做的,至於全域性貢獻直接開個字首和陣列記一下就好了,直接\(O(1)\)解決了
然後就沒啥了,哦,記得離散化一下\(size\)再拿來做下標,要不然可能有點卡常,最後貼個程式碼:
點選檢視程式碼
#include<bits/stdc++.h>
using namespace std;
#define int long long
#define ls lc[rt]
#define rs rc[rt]
#define pii pair<int,int>
#define fi first
#define se second
#define met(x) memset(x,0,sizeof x)
const int N=1e6+5;
int n,m,a[N],ans[N],sum1[N],sum2[N],w[N];
int x,y,z,l,r,k,t,sum,res,len,root[N];
int h[N],tot,b[N],size[N],wp[N],h1,h2;
struct sb{
int nxt,to,w;
}e[N];
inline void add(int x,int y,int z){
e[++tot]={h[x],y,z};
h[x]=tot;
}
inline int read(){
int s=0;char c=getchar_unlocked();
while(c<'0'&&c>'9')c=getchar_unlocked();
while(c>='0'&&c<='9'){s=(s<<1)+(s<<3)+(c^48);c=getchar_unlocked();}
return s;
}
inline void dfs(int x,int fa){
size[x]=a[x];
for(int i=h[x];i;i=e[i].nxt){
int y=e[i].to;
if(y==fa)continue;
dfs(y,x);
w[y]=e[i].w;
size[x]+=size[y];
}
b[x]=size[x];
// cout<<x<<" "<<b[x]<<endl;
}
struct tree{
int tot,w1[N<<2],w2[N<<2],lc[N<<2],rc[N<<2];
inline void clear(){tot=0;met(w1);met(w2);met(lc);met(rc);}
inline void tag(int rt,int v1,int v2){w1[rt]+=v1,w2[rt]+=v2;}
inline void pushup(int rt){w1[rt]=w1[ls]+w1[rs];w2[rt]=w2[ls]+w2[rs];}
inline void add(pii &a,pii b){a.fi+=b.fi;a.se+=b.se;}
inline void add(int &rt,int l,int r,int pos,int v1,int v2){
if(!rt)rt=++tot;
if(l==r)return tag(rt,v1,v2);
int mid=(l+r)>>1;
pos<=mid?add(ls,l,mid,pos,v1,v2):add(rs,mid+1,r,pos,v1,v2);
pushup(rt);
}
inline pii query(int rt,int l,int r,int L,int R){
if(!rt)return {0,0};
if(L<=l&&r<=R)return {w1[rt],w2[rt]};
int mid=(l+r)>>1;pii res={0,0};
if(L<=mid)add(res,query(ls,l,mid,L,R));
if(R>mid)add(res,query(rs,mid+1,r,L,R));
return res;
}
inline int merge(int x,int y){
if(!x||!y)return x^y;
w1[x]+=w1[y];w2[x]+=w2[y];
lc[x]=merge(lc[x],lc[y]);
rc[x]=merge(rc[x],rc[y]);
return x;
}
}T1;
struct shu{
//支援單點修改,字首查詢
int c1[N],c2[N];
inline int lb(int x){return x&-x;}
inline void clear(){for(int i=1;i<=n;i++)c1[i]=c2[i]=0;}
inline void add(int x,int w1,int w2){while(x<=len)c1[x]+=w1,c2[x]+=w2,x+=lb(x);}
inline pii ask(int x){pii res={0,0};while(x){res.fi+=c1[x],res.se+=c2[x],x-=lb(x);}return res;}
}T2;
//ans=size[x]*e[i].w(size[x]<=totsize/2)+(totsize-size[x])*e[i].w(size[x]>totsize/2)
//ans=size[x]*e[i].w(<=) -size[x]*e[i].w(>) +totsize*((size[x]>totsize/2)*e[i].w)
//開一個下標為size的值域線段樹儲存兩個資訊 e[i].w e[i].w*size[x]
inline void get_ans(int x,int fa,int w){
T1.add(root[x],1,len,wp[x],w,size[x]*w);
T2.add(wp[x],w,size[x]*w);ans[x]=0;
h1+=w;h2+=size[x]*w;
for(int i=h[x];i;i=e[i].nxt){
int y=e[i].to;
if(y==fa)continue;
get_ans(y,x,e[i].w);
//子樹內
pii res=T1.query(root[y],1,len,upper_bound(b+1,b+1+len,size[y]/2)-b,len);
ans[y]+=res.fi*size[y]-res.se//size>size[y]/2的貢獻
+T1.w2[root[y]]-res.se;//size<size[y]/2的貢獻
//鏈上
int sz=size[1]-size[y];
int pos=upper_bound(b+1,b+1+len,sz/2+size[y])-b;
res=T2.ask(pos-1);
ans[y]+=res.se-res.fi*size[y]+(h1-res.fi)*size[y]+(h1-res.fi)*sz-(h2-res.se);
//全域性貢獻(對於size==size[1]-size[y])(一會再減去算重的貢獻)
pos=upper_bound(b+1,b+1+len,sz/2)-b;
ans[y]+=sum2[pos-1]//size<sz/2的貢獻
+sz*(sum1[len]-sum1[pos-1])-(sum2[len]-sum2[pos-1]);//size>sz/2的貢獻
//減去子樹裡重複的貢獻
res=T1.query(root[y],1,len,pos,len);
ans[y]-=res.fi*sz-res.se//size>size[y]/2的貢獻
+T1.w2[root[y]]-res.se;//size<size[y]/2的貢獻
//減去鏈上重複的貢獻
res=T2.ask(pos-1);
ans[y]-=res.se+(h1-res.fi)*sz-(h2-res.se);
T1.merge(root[x],root[y]);
}
T2.add(wp[x],-w,-size[x]*w);
h1-=w;h2-=size[x]*w;
}
signed main(){
freopen("banking.in","r",stdin);
freopen("banking.out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
t=read();
while(t--){
n=read();tot=0;
T1.clear();T2.clear();
for(int i=1;i<=n;i++)root[i]=h[i]=0;
for(int i=1;i<=n;i++)a[i]=read();
for(int i=1;i<n;i++){
x=read(),y=read(),z=read();
add(x,y,z);add(y,x,z);
}
dfs(1,0);
sort(b+1,b+1+n);
len=unique(b+1,b+1+n)-b-1;
for(int i=1;i<=n;i++)sum1[i]=sum2[i]=0;
for(int i=1;i<=n;i++){
wp[i]=lower_bound(b+1,b+1+len,size[i])-b;
sum1[wp[i]]+=w[i];sum2[wp[i]]+=w[i]*size[i];
}
for(int i=1;i<=len;i++)sum1[i]+=sum1[i-1],sum2[i]+=sum2[i-1];
get_ans(1,0,0);
int ANS=1e18;
for(int i=2;i<=n;i++)ANS=min(ANS,ans[i]);
cout<<ANS<<'\n';
}
return 0;
}