解析記憶體中的高效能圖結構

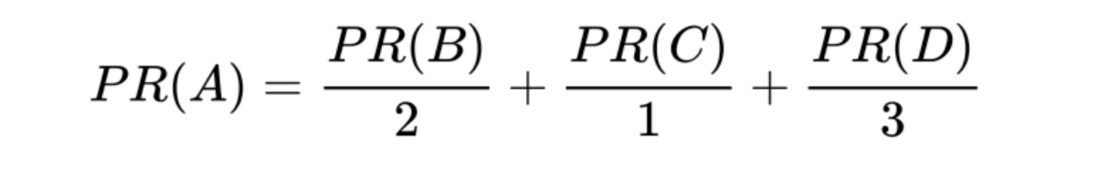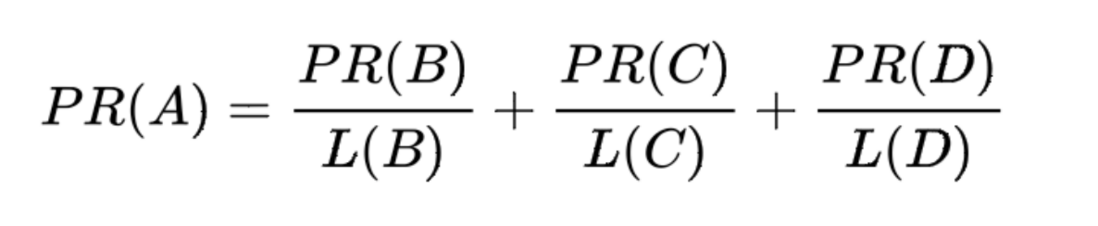
在進行各種圖處理、圖計算、圖查詢的時候，記憶體或是硬碟中如何儲存圖結構是一個影響效能的關鍵因素。本文主要分析了幾種常見的記憶體圖結構，及其時間、空間複雜度，希望對你有所啟發。

通常來說，對於圖結構的幾種常見的基礎操作：

插入一個點
插入一個邊
刪除一個邊
刪除一個點的全部鄰邊
找到一個點的全部鄰邊
找到一個點的另一個鄰點
全圖掃描
獲取一個點的入度或者出度

這些圖相關的操作，除了要關心時間複雜度之外，需要考慮空間佔用的問題。

對於大多數實時讀寫型的系統，增刪改查的效能問題會比較重要，它們比較關註上面 1-6 的操作；對於部分密集計算的系統，對批次讀取的效能會比較重視，側重上面 5-8 的操作。

不過遺憾的是，無論是常規的圖查詢，還是進階的圖計算，根據 RUM 猜想[1]，讀快、寫快、又省空間這樣”既要又要也要”的好事是不存在的。

下面，我們介紹幾個資料結構並給出少量的定量分析。

我們先從三個典型的方案（鄰接矩陣、壓縮稀疏矩陣和鄰接表）說起，再介紹幾種近幾年的研究的變種結構 PCSR、VCSR、CSR++。

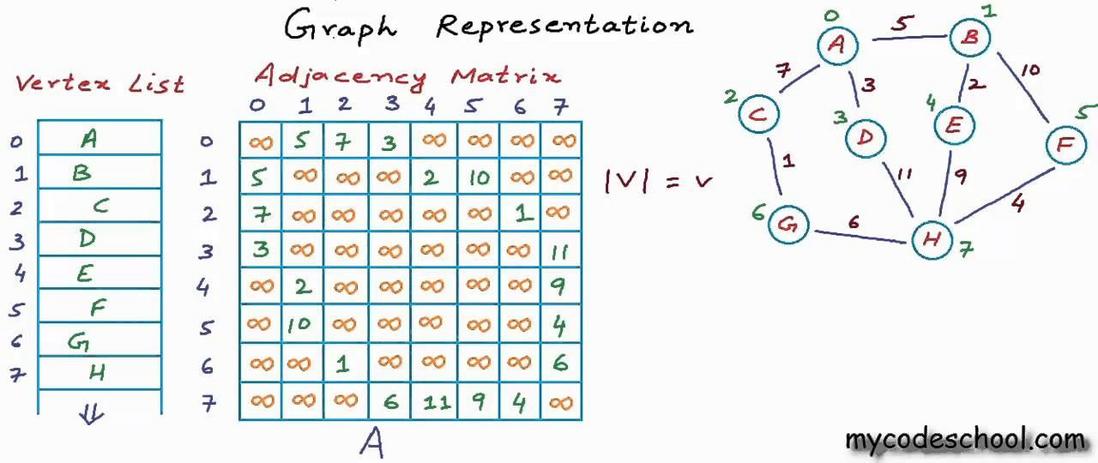
鄰接矩陣 Adjacency Matrix

用矩陣來表示圖結構是大學裡資料結構課程中都學過的知識，也是一種非常直觀的辦法。

點 i 與點 j 之間有一條邊，等價對應於矩陣上 $M_{ij}$ 為 1。當然，這裡的點 ID 是需要連續排列無空洞。

用矩陣來表示圖結構有明顯的好處，可以複用大量線性代數的研究成果：比如圖上模式匹配類的問題等價於矩陣的相乘。

下面是一個模式匹配問題，它的大體意思是在全圖上尋找這樣一種圖結構：

Match (src)-[friend * 2..4]->(fof)
WHERE src.age > 30
RETURN fof

對於這樣一個問題可以直接對應右邊的矩陣操作：

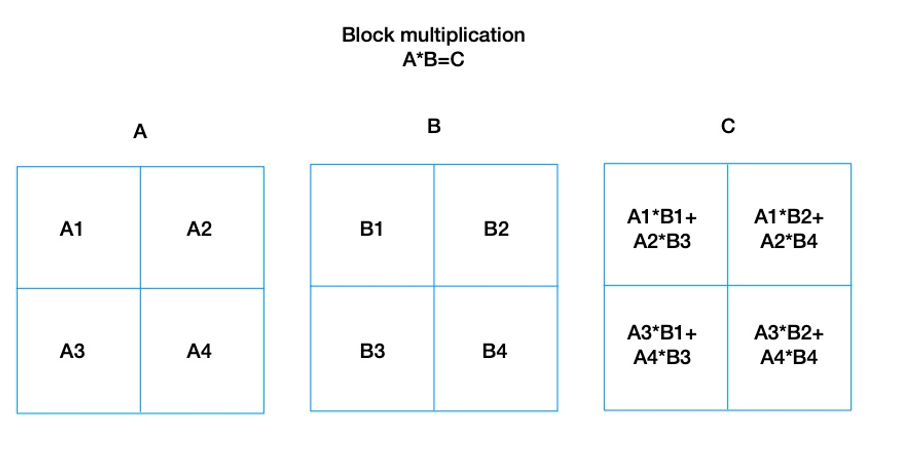
比如，2 跳遍歷等價於矩陣 F 自乘；2 - 4 跳遍歷分別等價於 F^2、F^3、F^4；取屬性等價於乘以一個過濾矩陣。

更進一步，由於矩陣操作是天生可以分塊並行加速，這在效能上有極大的優勢。

下面，我們對鄰接矩陣操作進行一個簡單的定量分析

操作	時間複雜度	備註
插入一個點	O(n^2)	對於矩陣來說，增加一個點意味著整個矩陣的維度增加，通常需要另外開闢一塊空間
插入一個邊	O(1)	增加一個邊只是將對應的位置置 1
刪除一個邊	O(1)	置0
刪除一個點的全部鄰邊	O(n)	對於某個點所有出邊的刪除對應某一行的置0。入邊對應某一列，可以批次操作
找到一個點的全部鄰邊	O(n)
找到一個點的給定鄰點	O(1)
全圖掃描	O(n^2)

其中，n=|V|，m=|E|。

最佳化上，批次操作（CPU Cache/SSD block）可以線性增加效能，例如 O(n) 可以降低到 O(n/B)，但不影響定量分析。

由於絕大多數圖結構是極其稀疏的，因此簡單用鄰接矩陣來表示圖結構，其記憶體會有誇張的浪費。更為嚴重的是，當有多種邊型別時，每種邊型別各需要一個鄰接矩陣。這使得裸用矩陣在實際情況中只能處理很小資料量的場景。當然，對於現代伺服器動輒幾百 G 的記憶體，如果只有幾億點邊的資料量，像是 twitter2010，這並不會是很嚴重的問題。但大多數情況下，條件允許的話，大家還是希望找到一些更加經濟的結構。

壓縮稀疏矩陣 CSR/CSC

壓縮稀疏矩陣是一種非常流行和緊湊的圖結構表示方式，大多數圖計算系統都採用 CSR。

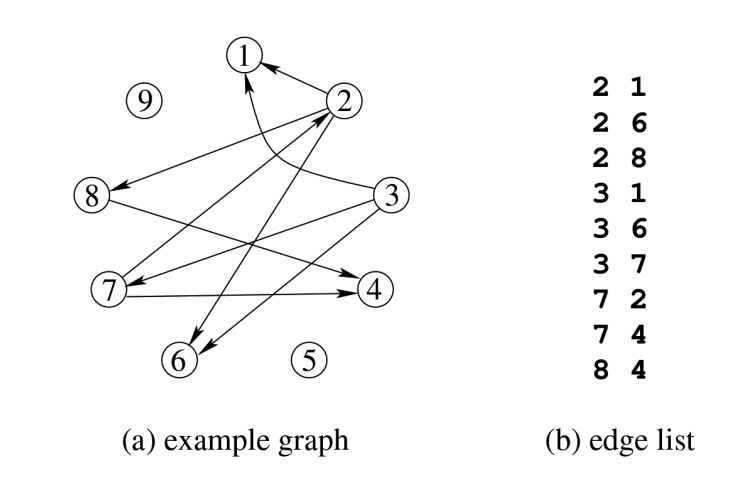
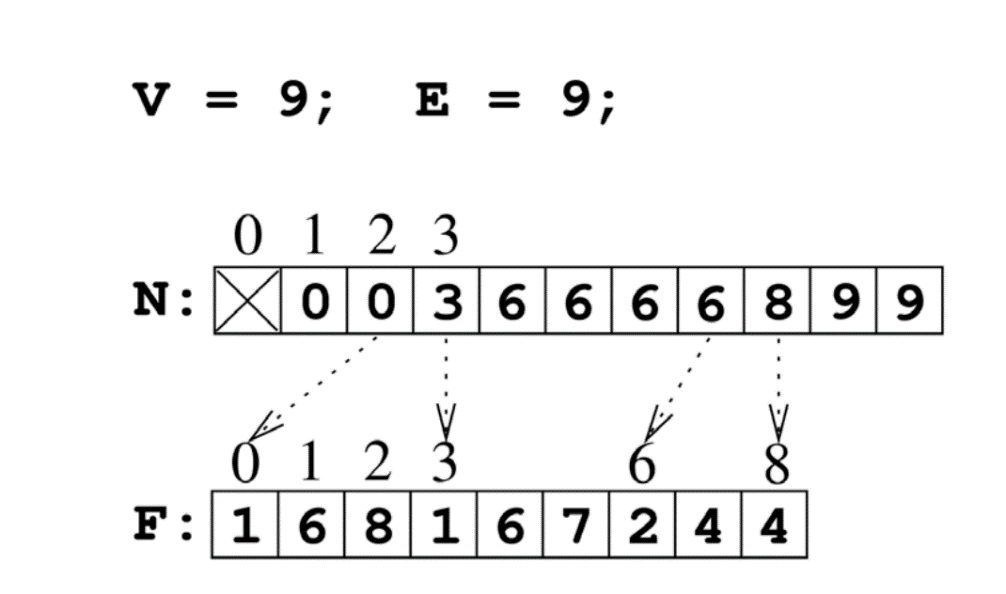
這裡簡單介紹一下 CSR 的結構：

對於點 IDx，取鄰居 ID 就是 F[N[x]] 到 F[N[x+1]-1]。

例如，查詢點 ID2 的鄰居，對應為 F[N[2]] 到 F[N[2+1]-1]，對應到上圖也即 1 6 8。查詢點 ID7 的鄰居，對應為 F[N[7]] 到 F[N[7+1]-1]，也就是 2 和 4。

另外，CSR 記錄的僅是出邊的資訊，如果要考慮入邊就使用 CSC，其原理是類似的。

操作	時間複雜度	備註
插入一個點	O(1)	在點向量尾部增加
插入一個邊 <u,v>	O(m+n)	邊向量，從 u 對應的鄰居開始，都向後移動一位；點向量，從 u 對應位置開始每個值加 1
刪除一個邊	O(m+n)	插入邊的逆過程
刪除一個點 v 的全部鄰邊	O(m+n)	邊向量移動 deg(v) 位，點向量 u 對應位置置 0
找到一個點的全部鄰邊	O(deg(v))
找到一個點的給定鄰點	O(log(deg(v)))	deg(v) 內的排序查詢
全圖掃描	O(m+n)

CSR 的空間佔用是 O(|V|+|E|)，在空間節省和順序查詢上是極其高效的。但在大量插入時，壓縮稀疏矩陣和鄰接矩陣一樣，需要重新開闢空間，效率很低。所以，它適合於計算密集場景但不適合增改頻繁的場景。

CSR 還有一個顯著的優點是可以快速獲取每個點的出入度，只要計算 N[x+1]-N[x]，這在判斷一些點是否為超級節點時很方便。如果不是稀疏矩陣的話，通常會用另外一個單獨的結構來記錄出入度。

此外，CSR 不容易實現併發修改，其每次插入都需要對兩個向量進行位移，這並不高效。

這裡推薦兩個相關的開源專案，可以進一步瞭解下 CSR 的使用：

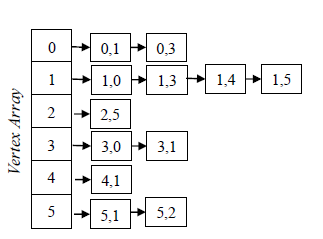
鄰接連結串列 Adjacency List

和基於矩陣的方式不同，鄰接連結串列 AL 空間上有優勢，但對於邊的讀寫上會略微慢一點（指標在記憶體中不能連續移動）。AL 的做法是把鄰邊（出邊）用 list 或者有序 list 的方式串連起來。由此延伸的一個變種是鄰邊從 list 改為 array。

操作	時間複雜度	備註
插入一個點	O(1)	尾插入
插入一個邊 <u,v>	O(log(deg(u)))	有序 list
刪除一個邊	O(log(deg(u)))
刪除一個點 v 的全部鄰邊	O(1)
找到一個點的全部鄰邊	O(deg(u))
找到一個點的給定鄰點	O(log(deg(u)))
全圖掃描	O(n+m)

AL 相比 CSR 通常不能直接獲得點的出入度，可以透過可以單獨維護一個欄位實現該功能。

此外，鄰接表並不需要 ID 連續排布，對於頻繁增刪點的場景特別友好。AL 對於併發修改的支援也更友好，天然在點級別有並行度。當然，對於超級節點，直接用 list 的方式，還是會有些效能的問題要考慮；最佳化上可能會進一步改造成 Blocked list 的方式，可以帶來更好的資料區域性性和細顆粒度。

由於 ID 不用嚴格連續排布，AL 的一個常見變種就是 Tree。

Tree

在這種結構中，一個點和其所有的鄰邊被建模成了 key-value，key 是點 ID，value 是所有鄰邊的編碼。Key 透過 Tree 的方式組織在一起。這裡的樹可以是 B-Tree 等各變種 Tree。雖然本文沒有討論圖屬性，但 value 中也是可以存放 value。

操作	時間複雜度	備註
插入一個點	O(log(n))
插入一個邊 <u,v>	O(deg(u) log(n))
刪除一個邊	O(deg(u) log(n))
刪除一個點 v 的全部鄰邊	O(log(n))
找到一個點的全部鄰邊	O(deg(u) log(n))
找到一個點的給定鄰點	O(log(n deg(u))
全圖掃描	O(n+m)

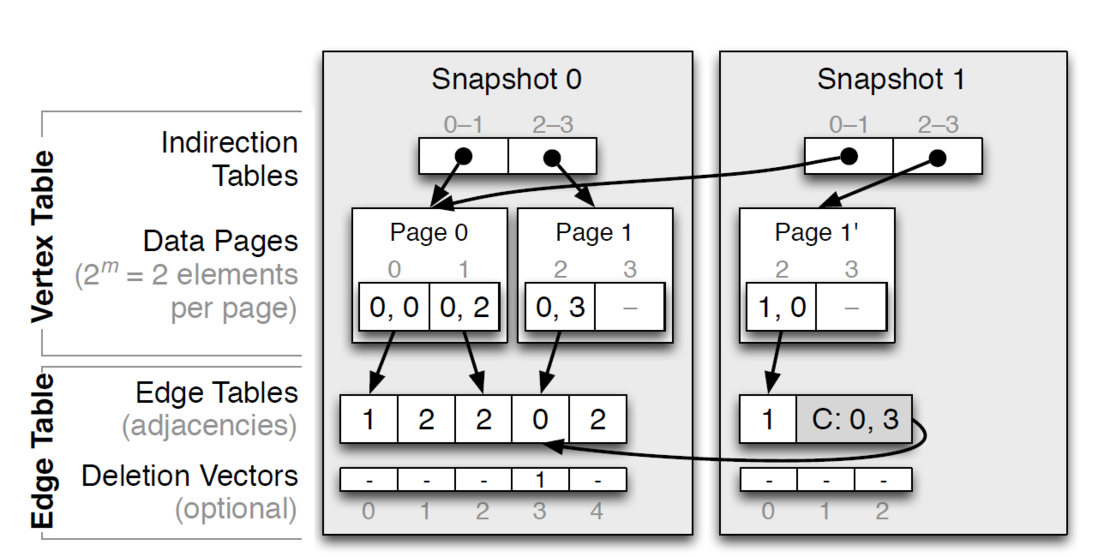
為了控制訪問顆粒度，每個葉子通常會被限定為固定的大小（頁）。這就是在資料庫類系統裡面最常見的辦法 B-tree。為了增改方便，也可以把每頁的 in-place update 改成 Copy-On-Write 的方式；一個典型的代表就是 LLAMA[2]，但這種多版本的讀取通常會需要更多的空間，並且當有大量累積修改時，需要定期的多版本合併以降低跨快照讀。某種程度上，它和 LSM-Tree 的思路有些接近。

基於 CSR 的變種 PCSR 和 VCSR

由於 CSR 在空間和讀效能上有很大的優勢，但在插入時的耗時和空間上都很弱，因此本節幾個變種的主要目的都是為了改善其弱項，大體思路都是分塊和 buffer。

在 CSR 的邊向量進行增刪時可以注意到，主要耗時是在對於向量的元素位移上。因此，一個直觀的思路是預留一些插入空白位，在刪除時也不立刻回收這些空白。

而分塊思想，是指將一些區域性資料放在同一個分塊內，例如 Tree 中每個 page 就是一種分塊的方式。與此對應的是，buffer 空白之間的連續區域。

PCSR

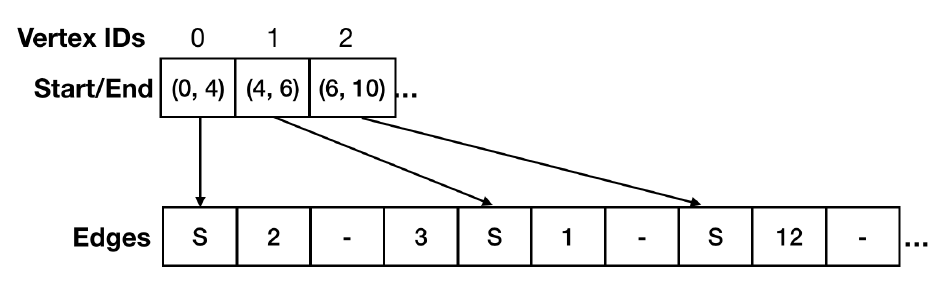
PCSR [3]的基本思想是：對於點向量，其元素從一個值改為對應邊向量中對應鄰邊位置的 <起點,終點>。而對於邊向量，在這些分塊所對應邊界放置哨兵 sentinel，上圖中的 S，上圖的 “-“ 對應預留插入位置留空。

事實上，原文中，對於邊向量，其本質是實現為一個 B-Tree，本文先簡化成一個 Array。

操作	時間複雜度	備註
插入一個點	O(1)	直接在點向量和邊向量的尾插入
插入一個邊 <u,v>	O(log(deg(u))	邊向量對應分片的二分+空位查詢
刪除一個邊	O(log(deg(u))
刪除一個點v的全部鄰邊	O(1)	邊向量對應分片置空，點向量對應 ID 位置置空
找到一個點的全部鄰邊	O(deg(u))
找到一個點的給定鄰點	O(log(deg(u))
全圖掃描	O(n+m)

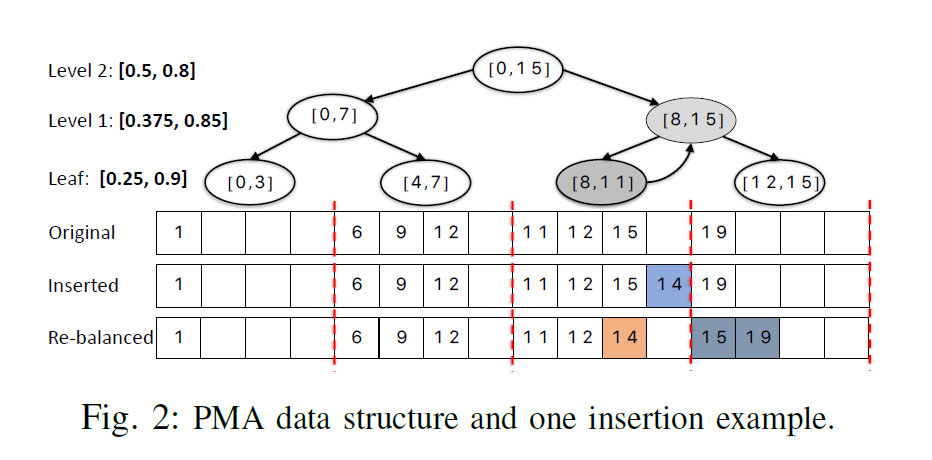
可以看到，PCSR 的預留位置多少都是需要重平衡，不能過多也不能不足。特別是大批次增刪時，對預留位置的處理會是一個較重的操作。

此外，如果把 PMA 的 B-Tree 以及需要 rebalance 的本質考慮進去，其和前述 Tree 方式的區別並不是很大。

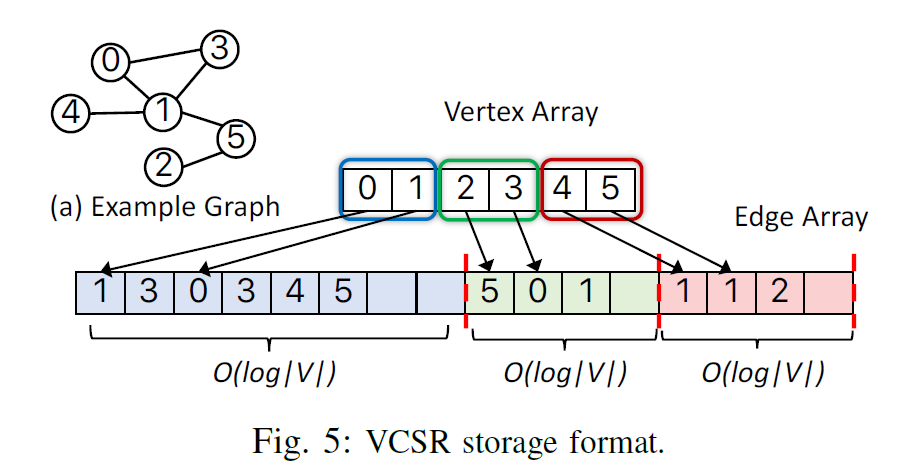
VCSR

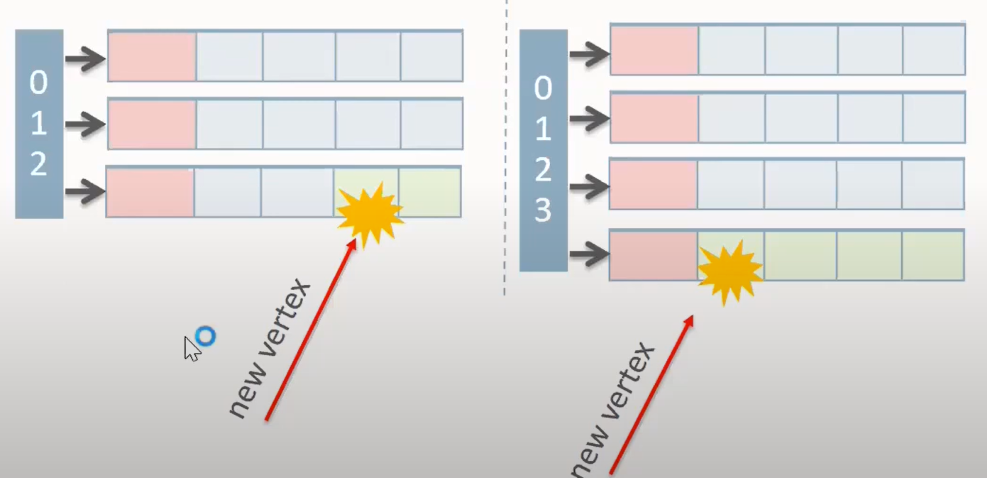
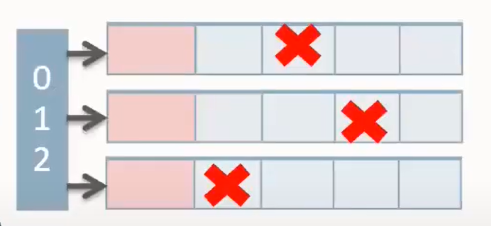
VCSR[4]主要是對 PCSR 的一個改進，其樸素思想是 PCSR 的留空是均勻的，而大多數圖結構的出入度，是存在 20-80 這樣的冪率特徵，而 PCSR 的一個主要痛點是頻繁的 rebalance。VCSR 的做法是為每個分塊預留空間正比於其分塊內的點的數量，即：邊向量中，一個分塊內，如果點的數量多，就多預留一些空位。在直覺上，點數量多時，其分塊對應的邊插入會更多一些，這樣可以減少 rebalance 的頻率。

此外，VCSR 還有些版本號之類的最佳化。

CSR++

事實上，CSR++[5]在設計上其實更接近一種 AL/Tree 的變種，而不是 CSR。它主要有三個方面的最佳化：

第一，對於 Vertex Array 再分段，將一個大的 Array 拆成多段，這樣可以有更細的讀寫顆粒度。透過 段 ID + 點 ID 來定位每個點和其鄰邊。
第二，Vertex Array 中每個元素，除了記錄點 ID 之外，對於鄰邊數量很少的點，直接把鄰居 ID 也對齊地塞 inline 進去。

對於大多數的點，其鄰邊就不需要單獨的 Edge Array 來儲存了。

可以看到這種方式在圖比較稀疏的時候，對於 CPU Cache 掃描是很友好的。

第三，對於每個點的鄰邊，採用copy-on-write、標記刪除等常見的最佳化辦法，構建成類似 std::vector 結構。

小結

最後，由於在圖查詢、圖儲存和圖計算不同場景下，對於圖結構的讀寫掃描和生命週期都有些不同的要求，不同的資料結構也有不同的優劣。

當然，本文只是討論了圖結構可以放在記憶體中的情況。當不得不把部分資料放在硬碟上時，問題就完全不同了。當然本文也沒有討論不同 CPU 對於不同距離記憶體的效能差異 NUMA，或者跨程式通訊帶來的影響。

延伸閱讀

最後，我們來瞭解下在圖計算/圖演演算法上的圖操作。

圖演演算法中的圖操作

在圖計算中，存在多種圖結構演演算法，可能會涉及多種基礎操作。

中心性 Centrality Algorithms，一種衡量一個節點在整個網路圖中所在中心程度的演演算法，包括：度中心性、接近中心性、介數中心性等，會涉及“找到一個點的全部鄰邊”、“找到一個點的另一個鄰點”、“全圖掃描”的操作組合。

度中心性透過節點的度數，即關聯的邊數來刻畫節點的受歡迎程度，這將會要求找到一個點的所有鄰邊。
接近中心性，透過計算每個節點到全圖其他所有節點的路徑和來刻畫節點與其他所有節點的關係密切程度，這將會要求進行全圖掃描，查詢點和圖中所有點的路徑資訊。
介數中心性，則用於衡量一個頂點出現在其他任意兩個頂點對之間最短路徑上的次數，從而來刻畫節點的重要性，這將會要求進行全圖掃描，找到一個點和它的鄰點及路徑資訊

PageRank，又稱網頁排名、谷歌左側排名，是一種由搜尋引擎根據網頁之間相互的超連結計算的技術作為網頁排名的要素之一的排名方法。它以 Google 公司創辦人拉里·佩奇 Larry Page 之姓來命名。Google 用它來體現網頁的相關性和重要性，在搜尋引擎最佳化操作中是經常被用來評估網頁最佳化的成效因素之一。一般來說，PageRank 的值越高，表示其被很多其他網頁連結到，說明它的重要性很高；而如果一個 PageRank 很高的網頁連結到其他網頁，被連結的網頁的 PageRank值也會隨之提高。PageRank 的計算過程如下：

假設由 4 個網頁組成的集合：A、B、C、D，每個頁面的初始 PageRank 值相同，為了滿足機率值為 0-1 之間，假設這個值為 0.25。

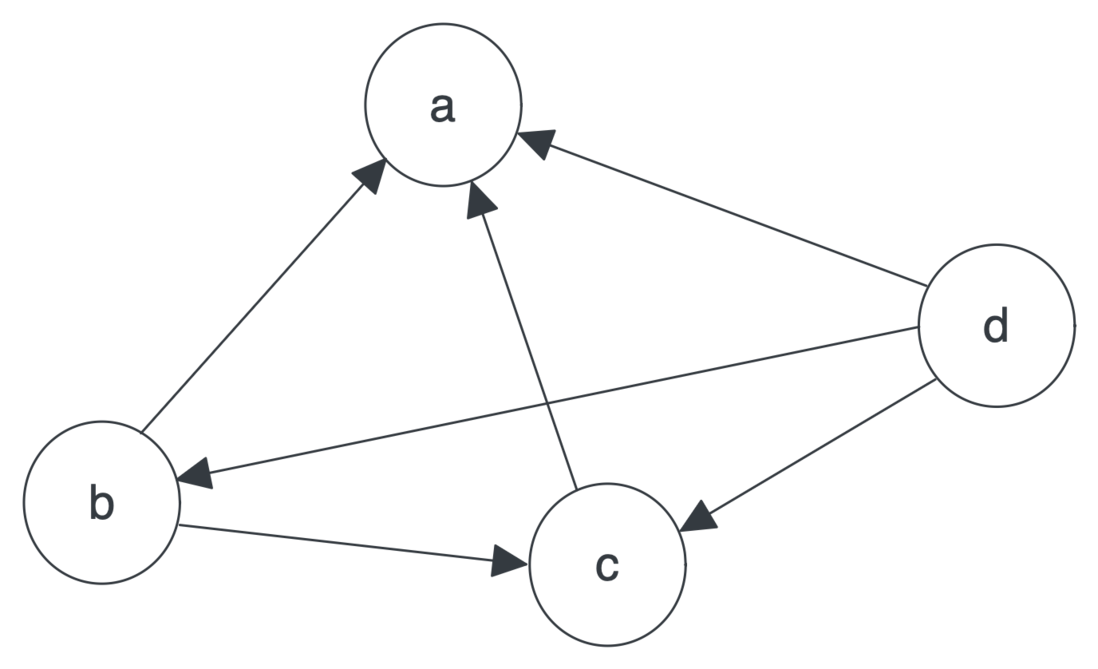
如果所有頁面都只連結至 A，如下圖，則 A 點的值將是 B、C、D 的 PageRank 值的和。

倘若是下圖這種圖結構：

B 連結到 C，D 連結到 B 和 C，A 點的值計算的方式如下：

這裡的 2、1、3，分別是 B 點對外連結的 2 條邊，C 點對外連結的 1 條邊，D 點對外連結的 3 條邊。

換句話說，演演算法將根據每個頁面連出總數平分該頁面的 PR 值，並將其加到其所指向的頁面：

最後，所有這些 PR 值被換算成百分比形式再乘上一個修正係數。

由於“沒有向外連結的網頁”傳遞出去的 PR 值會是0，這時候如果遞迴的話，會導致指向它的頁面的 PR 值的計算結果同樣為零，所以 PageRank 會賦給每個頁面一個最小值。

因此，一個頁面的 PR 值直接取決於指向它的的頁面。如果在最初給每個網頁一個隨機且非零的 PR 值，經過重複計算，這些頁面的 PR 值會趨向於某個定值，也就是處於收斂的狀態，即最終結果。

簡單來說，大多數迭代圖計算模型都是基於“找到一個點的全部鄰邊”、“找到一個點的另一個鄰點”操作。

AIGC 小課堂

在 AIGC 小課堂部分，我們會用 NebulaGraph 接入的 aibot 來講解下文中的部分概念。你如果對 chatgpt 或者是 aibot 有興趣，可以來 https://discuss.nebula-graph.com.cn/ 向 aibot 提出你的要求。

參考文獻

Athanassoulis, M., Kester, M. S., Maas, L. M., et al. (2016). Designing Access Methods: The RUM Conjecture. In EDBT (pp. 461-466).
Macko, P., Marathe, V. J., Margo, D. W., et al. (2015). Llama: Efficient Graph Analytics Using Large Multiversioned Arrays. In 2015 IEEE 31st International Conference on Data Engineering (pp. 363-374). IEEE.
Wheatman, B., & Xu, H. (2018). Packed Compressed Sparse Row: A Dynamic Graph Representation. In 2018 IEEE High Performance Extreme Computing Conference (HPEC) (pp. 1-7). IEEE.
Islam, A. A. R., Dai, D., & Cheng, D. (2022). VCSR: Mutable CSR Graph Format Using Vertex-Centric Packed Memory Array. In 2022 22nd IEEE International Symposium on Cluster, Cloud and Internet Computing (CCGrid) (pp. 71-80). IEEE.
Firmli, S., Trigonakis, V., Lozi, J. P., et al. (2020). CSR++: A Fast, Scalable, Update-Friendly Graph Data Structure. In 24th International Conference on Principles of Distributed Systems (OPODIS'20).