1、方差:就是和中心偏離的程度!用來衡量一批資料的波動大小(即這批資料偏離平均數的大小)並把它叫做這組資料的方差。標準差是方差平方根。
公式:
舉例:比如1.2.3.4.5 這五個數的平均數是3
方差就是: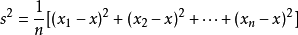
即:1/5[(1-3)²+(2-3)²+(3-3)²+(4-3)²+(5-3)²]=2
2、kmeans是最簡單的聚類演算法之一,但是運用十分廣泛。kmeans一般在資料分析前期使用,選取適當的k,將資料分類後,然後分類研究不同聚類下資料的特點。
3、正態分佈(Normal distribution)又名高斯分佈(Gaussian distribution),是一個在數學、物理及工程等領域都非常重要的機率分佈,在統計學的許多方面有著重大的影響力。若隨機變數X服從一個數學期望為μ、方差為σ^2的高斯分佈,記為N(μ,σ^2)。
4、 表示求和:∑讀音為sigma,英文意思為Sum。其中i表示下界,n表示上界, k從i開始取數,一直取到n,全部加起來。
5、對數函式:如果ax=N(a>0,且a≠1),那麼數x叫做以a為底N的對數,記作x=logaN,讀作以a為底N的對數,其中a叫做對數的底數,N叫做真數。
圖形如下:
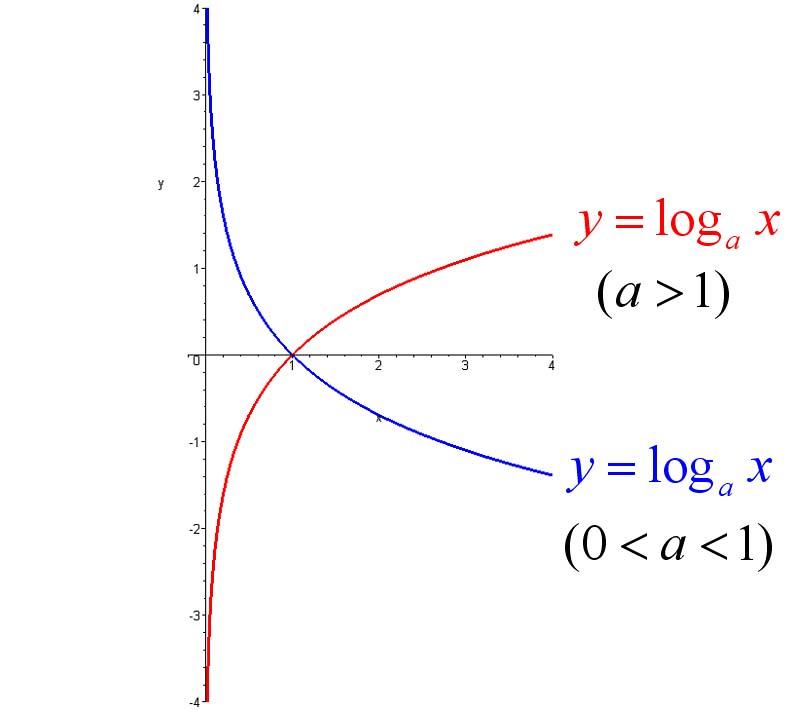
6、自然對數:以常數e為底數的對數叫做自然對數,記作lnN(N>0)。它的含義是單位時間內,持續的翻倍增長所能達到的極限值。
自然對數的底數e是由一個重要極限給出的。我們定義:當n趨於無限時,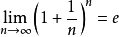 。
。
e是一個無限不迴圈小數,其值約等於2.718281828459…,它是一個超越數。
7、最小二乘法
殘差:設yi是被解釋變數的第i次樣本觀測值, yi^是相應的第 i 次樣本估計值。將 yi 與 yi^之間的偏差記作ei稱 ei為第 i 次樣本觀測值的殘差。
最小二乘準則:使全部樣本觀測值的殘差平方和達到最小。
8、導數:導數是函式的區域性性質。一個函式在某一點的導數描述了這個函式在這一點附近的變化率。如果函式的自變數和取值都是實數的話,函式在某一點的導數就是該函式所代表的曲線在這一點上的切線斜率。導數的本質是透過極限的概念對函式進行區域性的線性逼近。例如在運動學中,物體的位移對於時間的導數就是物體的瞬時速度。
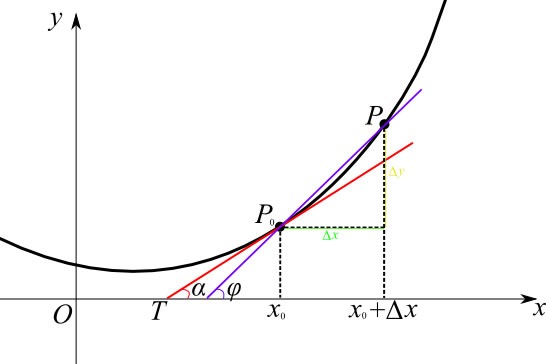
9、基本初等函式:http://baike.baidu.com/view/363955.htm
10、各分步函式與圖形
二項分步
多項分步
正態分步
伯努力試驗
T分步
均勻分步
泊松分步
11、泊松分步:是一種統計與機率學裡常見到的離散機率分佈。
泊松分佈適合於描述單位時間內隨機事件發生的次數。如某一服務設施在一定時間內到達的人數,電話交換機接到呼叫的次數,汽車站臺的候客人數,機器出現的故障數,自然災害發生的次數等等。
12、伯努力試驗和二項分步:(Bernoulli experiment)是在同樣的條件下重複地、相互獨立地進行的一種隨機試驗。其特點是該隨機試驗只有兩種可能結果:發生或者不發生。
二項分佈:一般地,在n次獨立重複試驗中,用ξ表示事件A發生的次數,如果事件發生的機率是P,則不發生的機率 q=1-p,N次獨立重複試驗中發生K次的機率是:
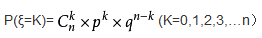
那麼就說ξ服從二項分佈。.其中P稱為成功機率。
記作:ξ~B(n,p)
期望:Eξ=np
方差:Dξ=npq
13、排列:從n個不同元素中取出m(m≤n)個元素的所有排列的個數,叫做從n個不同元素中取出m個元素的排列數,用符號Anm(或Pnm,或nPm)表示。
公式: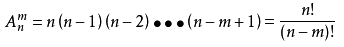
14、組合:一般地,從m個不同的元素中,任取n(n≤m)個元素為一組,叫作從m個不同元素中取出n個元素的一個組合。
公式: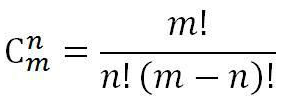
15、階乘:一個正整數的階乘(英語:factorial)是所有小於及等於該數的正整數的積,並且有0的階乘為1。自然數n的階乘寫作n!。
16、神經網路演算法:人工神經網路也就是一個普通的分類器而已,解決那些人類可以解決的Task。機器學習模型都只能解決兩個問題:特徵選擇(Feature Selection)和函式擬合(Function Fitting)
17、箱形圖(箱尾圖):是一種用作顯示一組資料分散情況資料的統計圖。
(1)箱形圖為我們提供了識別異常值的一個標準:異常值被定義為小於Q1-1.5IQR或大於Q3+1.5IQR的值。
(2)判斷資料偏態和尾重。
(3)比較幾批資料的形狀
18、支援向量機(SVM):超級通俗的解釋:支援向量機是用來解決分類問題的。
先考慮最簡單的情況,豌豆和米粒,用篩子很快可以分開,小顆粒漏下去,大顆粒保留。
用一個函式來表示就是當直徑d大於某個值D,就判定為豌豆,小於某個值就是米粒。
d>D, 豌豆
d<D, 米粒
在數軸上就是在d左邊就是米粒,右邊就是綠豆,這是一維的情況。
但是實際問題沒這麼簡單,考慮的問題不單單是尺寸,一個花的兩個品種,怎麼分類?
假設決定他們分類的有兩個屬性,花瓣尺寸和顏色。單獨用一個屬性來分類,像剛才分米粒那樣,就不行了。這個時候我們設定兩個值 尺寸x和顏色y。
我們把所有的資料都丟到x-y平面上作為點,按道理如果只有這兩個屬性決定了兩個品種,資料肯定會按兩類聚集在這個二維平面上。
我們只要找到一條直線,把這兩類劃分開來,分類就很容易了,以後遇到一個資料,就丟進這個平面,看在直線的哪一邊,就是哪一類。
比如x+y-2=0這條直線,我們把資料(x,y)代入,只要認為x+y-2>0的就是A類,x+y-2<0的就是B類。
以此類推,還有三維的,四維的,N維的 屬性的分類,這樣構造的也許就不是直線,而是平面,超平面。
一個三維的函式分類 :x+y+z-2=0,這就是個分類的平面了。
有時候,分類的那條線不一定是直線,還有可能是曲線,我們透過某些函式來轉換,就可以轉化成剛才的哪種多維的分類問題,這個就是核函式的思想。
例如:分類的函式是個圓形x^2+y^2-4=0。這個時候令x^2=a; y^2=b,還不就變成了a+b-4=0 這種直線問題了。
這就是支援向量機的思想。機的意思就是“演算法”,機器學習領域裡面常常用“機”這個字表示演算法。
支援向量意思就是資料集種的某些點,位置比較特殊,比如剛才提到的x+y-2=0這條直線,直線上面區域x+y-2>0的全是A類,下面的x+y-2<0的全是B類,我們找這條直線的時候,一般就看聚集在一起的兩類資料,他們各自的最邊緣位置的點,也就是最靠近劃分直線的那幾個點,而其他點對這條直線的最終位置的確定起不了作用,所以我姑且叫這些點叫“支援點”(意思就是有用的點),但是在數學上,沒這種說法,數學裡的點,又可以叫向量,比如二維點(x,y)就是二維向量,三維度的就是三維向量( x,y,z)。所以 “支援點”改叫“支援向量”,聽起來比較專業,NB。所以就是 支援向量機 了。