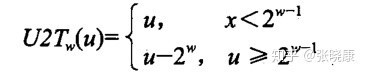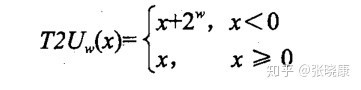一般來說,二進位制運算不滿足結合律和分配率,只有交換律可以用。
異或可以用結合律:a^(b^c)=(a^b)^c
與和或可以用分配律:a&(b|c)=(a|b)&(a|c)
乘法和加法可以用分配律:a*(b+c)=a*b+a*c
We consider the three most important representations of numbers. Unsigned
encodings are based on traditional binary notation, representing numbers greater
than or equal to 0. Two’s-complement encodings are the most common way to
represent signed integers, that is, numbers that may be either positive or negative.
Floating-point encodings are a base-2 version of scientific notation for representing real numbers. Computers implement arithmetic operations, such as addition
and multiplication, with these different representations, similar to the corresponding operations on integers and real numbers.
representation
美[ˌrɛprɪzɛnˈteʃən]
n. 表現;陳述
notation
美[noʊˈteɪʃn]
n. 記號,標記法
positive
美[ˈpɑːzətɪv]
adj. 陽性的;大於零的
negative
美[ˈneɡətɪv]
adj. 消極的;負的
scientific
美[ˌsaɪənˈtɪfɪk]
adj. 科學(上)的
arithmetic
美[əˈrɪθmətɪk]
adj. 算術的;運算的
multiplication
美[ˌmʌltɪplɪˈkeɪʃn]
n. [數]乘法,乘法運算
correspond
美[ˌkɔːrəˈspɑːnd]
v. 符合;相當於;通訊
2.1 Information Storage
In subsequent chapters, we will cover how the compiler and run-time system
partitions this memory space into more manageable units to store the different
program objects, that is, program data, instructions, and control information.
Various mechanisms are used to allocate and manage the storage for different
parts of the program. This management is all performed within the virtual address
space. For example, the value of a pointer in C—whether it points to an integer,
a structure, or some other program object—is the virtual address of the fifirst byte
of some block of storage. The C compiler also associates type information with
each pointer, so that it can generate different machine-level code to access the
value stored at the location designated by the pointer depending on the type of
that value. Although the C compiler maintains this type information, the actual
machine-level program it generates has no information about data types. It simply
treats each program object as a block of bytes and the program itself as a sequence
of bytes.
subsequent
美[ˈsʌbsɪkwənt]
adj. 後來的;隨後的
partition
美[pɑːrˈtɪʃn]
n. 隔離物;隔牆
various
美[ˈveriəs]
adj. 各種各樣的;千差萬別的
mechanism
美[ˈmekənɪzəm]
n. [生]機制,機能
associate
美[əˈsoʊsieɪt]
v. 聯想,聯絡;使與...有關係
maintain
美[meɪnˈteɪn]
v. 維持,保持
2.1.1 Hexadecimal Notation
A common task in working with machine-level programs is to manually con-
vert between decimal, binary, and hexadecimal representations of bit patterns.
Converting between binary and hexadecimal is straightforward, since it can be
performed one hexadecimal digit at a time. Digits can be converted by referring
to a chart such as that shown in Figure 2.2. One simple trick for doing the conver-
sion in your head is to memorize the decimal equivalents of hex digits A, C, and F.
The hex values B, D, and E can be translated to decimal by computing their values
relative to the fifirst three.
decimal
美[ˈdesɪml]
adj. 十進位的;小數的
hexadecimal
美[ˌhɛksəˈdɛsəməl]
adj. 十六進位制的
pattern
美[ˈpætərn]
n. 模式;範例
straightforward
美[ˌstreɪtˈfɔːrwərd]
adj. 簡單明瞭的
memorize
美[ˈmeməraɪz]
vt. 記住,熟記
equivalent
美[ɪˈkwɪvələnt]
n. 等同物;對應物
2.1.2 Data Sizes
Programmers should strive to make their programs portable across different
machines and compilers. One aspect of portability is to make the program insensi
tive to the exact sizes of the different data types. The C standards set lower bounds
on the numeric ranges of the different data types, as will be covered later, but there
are no upper bounds (except with the fifixed-size types). With 32-bit machines and
32-bit programs being the dominant combination from around 1980 until around
2010, many programs have been written assuming the allocations listed for 32-
bit programs in Figure 2.3. With the transition to 64-bit machines, many hidden
word size dependencies have arisen as bugs in migrating these programs to new
machines. For example, many programmers historically assumed that an object
declared as type int could be used to store a pointer. This works fifine for most
32-bit programs, but it leads to problems for 64-bit programs.
strive
美[straɪv]
vi. 力求;力爭
aspect
美[ˈæspekt]
n. 方面;樣子
insensitive
美[ɪnˈsɛnsɪtɪv]
adj. 無感覺的
bound
美[baʊnd]
n. 跳躍;界限
dominant
美[ˈdɑːmɪnənt]
adj. 佔支配地位的
combination
美[ˌkɑːmbɪˈneɪʃn]
n. 結合(體)
assume
美[əˈsuːm]
v. 假設,認為
allocation
美[ˌæləˈkeɪʃn]
n. 分配(物)
transition
美[trænˈzɪʃn]
n. 過渡,轉變,變遷
2.1.3 Addressing and Byte Ordering
At times, however, byte ordering becomes an issue. The first case is when
binary data are communicated over a network between different machines. A
common problem is for data produced by a little-endian machine to be sent to
a big-endian machine, or vice versa, leading to the bytes within the words being
in reverse order for the receiving program.
A second case where byte ordering becomes important is when looking at
the byte sequences representing integer data.
A third case where byte ordering becomes visible is when programs are
written that circumvent the normal type system.
vice
美[vaɪs]
n. 罪行;惡行
versa
美[ 'vɝsə]
adj. 反的
sequence
美[ˈsiːkwəns]
n. [數]數列,序列
circumvent
美[ˌsɜrkəmˈvent]
vt. 圍繞,包圍;用計防止
2.1.4 Representing Strings
A string in C is encoded by an array of characters terminated by the null (having
value 0) character. Each character is represented by some standard encoding, with
the most common being the ASCII character code. Thus, if we run our routine
show_bytes with arguments "12345" and 6 (to include the terminating character),
we get the result 31 32 33 34 35 00. Observe that the ASCII code for decimal digit
x happens to be 0x3x, and that the terminating byte has the hex representation
0x00. This same result would be obtained on any system using ASCII as its
character code, independent of the byte ordering and word size conventions. As
a consequence, text data are more platform independent than binary data.
obtained
美[əb'teɪnd]
v. 獲得
independent
美[ˌɪndɪˈpendənt]
adj. 獨立的
convention
美[kənˈvenʃn]
n. 習俗,慣例
consequence
美[ˈkɑːnsɪkwens]
n. 結果
2.1.5 Representing Code
A fundamental concept of computer systems is that a program, from the
perspective of the machine, is simply a sequence of bytes. The machine has no
information about the original source program, except perhaps some auxiliary
tables maintained to aid in debugging. We will see this more clearly when we study
machine-level programming in Chapter 3.
fundamental
美[ˌfʌndəˈmentl]
adj. 基礎的;根深蒂固的
perspective
美[pərˈspektɪv]
n. 觀點,看法
auxiliary
美[ɔːɡˈzɪliəri]
adj. 輔助的;備用的
maintain
美[meɪnˈteɪn]
v. 維持,保持
2.1.6 Introduction to Boolean Algebra
Claude Shannon (1916–2001), who later founded the field of information
theory, first made the connection between Boolean algebra and digital logic. In
his 1937 master’s thesis, he showed that Boolean algebra could be applied to the
design and analysis of networks of electromechanical relays. Although computer
technology has advanced considerably since, Boolean algebra still plays a central
role in the design and analysis of digital systems.
algebra
美[ˈældʒɪbrə]
n. 代數
thesis
美[ˈθiːsɪs]
n. 論文
electromechanical
美[ɪˌlektroʊmə'kænɪkəl]
adj. 電動機械的
considerably
美[kənˈsɪdərəblɪ]
adv. 相當,非常
2.1.7 Bit-Level Operations in C
One common use of bit-level operations is to implement masking operations,
where a mask is a bit pattern that indicates a selected set of bits within a word. As
an example, the mask 0xFF (having ones for the least signifificant 8 bits) indicates
the low-order byte of a word. The bit-level operation x & 0xFF yields a value
consisting of the least signifificant byte of x, but with all other bytes set to 0. For
example, with x = 0x89ABCDEF, the expression would yield 0x000000EF. The
expression ~0 will yield a mask of all ones, regardless of the size of the data
representation. The same mask can be written 0xFFFFFFFF when data type int is
32 bits, but it would not be as portable.
indicate
美[ˈɪndɪkeɪt]
v. 表明,暗示;指示
significant
美[sɪɡˈnɪfɪkənt]
adj. 重要的;顯著的
regardless
美[rɪˈɡɑːrdləs]
adv. 不管怎樣
representation
美[ˌrɛprɪzɛnˈteʃən]
n. 表現;陳述
2.1.8 Logical Operations in C
A second important distinction between the logical operators ‘&&’ and ‘||’
versus their bit-level counterparts ‘&’ and ‘|’ is that the logical operators do not
evaluate their second argument if the result of the expression can be determined
by evaluating the fifirst argument. Thus, for example, the expression a && 5/a will
never cause a division by zero, and the expression p && *p++ will never cause the
dereferencing of a null pointer.
distinction
美[dɪˈstɪŋkʃn]
n. 差別
versus
美[ˈvɜːrsəs]
prep. 與…相對
counterparts
美['kaʊntəpɑts]
n. 與對方地位相當的人
evaluate
美[ɪˈvæljueɪt]
v. 估計
determine
美[dɪˈtɜːrmɪn]
v. 查明;測定
division
美[dɪˈvɪʒn]
n. 除法
2.1.9 Shift Operations in C
The C standards do not precisely defifine which type of right shift should be
used with signed numbers—either arithmetic or logical shifts may be used. This
unfortunately means that any code assuming one form or the other will potentially
encounter portability problems. In practice, however, almost all compiler/machine
combinations use arithmetic right shifts for signed data, and many programmers
assume this to be the case. For unsigned data, on the other hand, right shifts must
be logical.
(右移:算術右移左邊補最高位的值,邏輯右移補0)
precisely
美[prɪˈsaɪsli]
adv. 精確地
arithmetic
美[əˈrɪθmətɪk]
adj. 算術的
potentially
美[pə'tenʃəli]
adv. 潛在地
encounter
美[ɪnˈkaʊntər]
v. 遭遇
combinations
美[kɒmbɪ'neɪʃnz]
n. 合作
2.2 Integer Representations
Figure 2.8 lists the mathematical terminology we introduce to precisely de-
fifine and characterize how computers encode and operate on integer data. This
terminology will be introduced over the course of the presentation. The fifigure is
included here as a reference.
mathematical
美[ˌmæθəˈmætɪkl]
adj. 數學的;精確的
terminology
美[ˌtɜːrmɪˈnɑːlədʒi]
n. 專門名詞;術語
precisely
美[prɪˈsaɪsli]
adv. 精確地
characterize
美[ˈkærəktəraɪz]
v. 使具有特點
terminology
美[ˌtɜːrmɪˈnɑːlədʒi]
n. 專門名詞;術語
presentation
美[ˌpriːzenˈteɪʃn]
n. 授予;頒獎儀式;介紹
reference
美[ˈrefrəns]
n. 提及
2.2.1 Integral Data Types
One important feature to note in Figures 2.9 and 2.10 is that the ranges are not
symmetric—the range of negative numbers extends one further than the range of
positive numbers. We will see why this happens when we consider how negative
numbers are represented.
symmetric
美[sɪ'metrɪk]
adj. 相稱性的,均衡的
2.2.2 Unsigned Encodings
In the fifigure, we represent each bit position i by a rightward-pointing blue bar of
length 2^i . The numeric value associated with a bit vector then equals the sum of
the lengths of the bars for which the corresponding bit values are 1.
associate
美[əˈsoʊsieɪt]
v. 聯想,聯絡
vector
美[ˈvɛktɚ]
n. 向量;航向
corresponding
美[ˌkɔːrəˈspɑːndɪŋ]
adj. 相應的,相關的
2.2.3 Two’s-Complement Encodings
For some programs, it is essential that data types be encoded using representations with specific sizes.
For example, when writing programs to enable a machine to communicate over the Internet according
to a standard protocol, it is important to have data types compatible with those specifified by the protocol.
We have seen that some C data types, especially long, have different ranges on different machines,
and in fact the C standards only specify the minimum ranges for any data type, not the exact ranges.
Although we can choose data types that will be compatible with standard representations on most
machines, there is no guarantee of portability.
essential
美[ɪˈsenʃl]
adj. 基本的;必不可少的
compatible
美[kəmˈpætəbl]
adj. 相容的;可共存的
guarantee
美[ˌɡærənˈtiː]
n. 保證;保修單
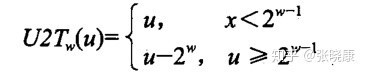
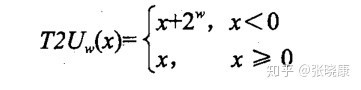
2.2.4 Conversions between Signed and Unsigned
C allows casting between different numeric data types. For example, suppose
variable x is declared as int and u as unsigned. The expression (unsigned) x
converts the value of x to an unsigned value, and (int) u converts the value of u
to a signed integer. What should be the effect of casting signed value to unsigned,
or vice versa? From a mathematical perspective, one can imagine several different
conventions. Clearly, we want to preserve any value that can be represented in
both forms. On the other hand, converting a negative value to unsigned might yield
zero. Converting an unsigned value that is too large to be represented in two’s complement form might yield TMax. For most implementations of C, however,
the answer to this question is based on a bit-level perspective, rather than on a
numeric one.
declared
美[dɪˈklerd]
v. 宣佈
vice versa
美[ˌvaɪs ˈvɜːrsə]
adv. 反過來也一樣;反之亦然
perspective
美[pərˈspektɪv]
n. 透鏡,望遠鏡;觀點,看法
preserve
美[prɪˈzɜːrv]
v. 保持;保護
2.2.5 Signed versus Unsigned in C
Some possibly nonintuitive behavior arises due to C’s handling of expres-
sions containing combinations of signed and unsigned quantities. When an op-
eration is performed where one operand is signed and the other is unsigned, C
implicitly casts the signed argument to unsigned and performs the operations
assuming the numbers are nonnegative. As we will see, this convention makes
little difference for standard arithmetic operations, but it leads to nonintuitive
results for relational operators such as < and >. Figure 2.19 shows some sample
relational expressions and their resulting evaluations, when data type int has a
32-bit two’s-complement representation. Consider the comparison -1 < 0U. Since
the second operand is unsigned, the fifirst one is implicitly cast to unsigned, and
hence the expression is equivalent to the comparison 4294967295U < 0U (recall
that T2Uw(−1) = UMaxw), which of course is false. The other cases can be under-
stood by similar analyses.
intuitive
美[ɪnˈtuːɪtɪv]
adj. 直覺的
operand
美[ˈɑpərænd]
n. 運算元
implicitly
美[ɪmˈplɪsɪtlɪ]
adv. 含蓄地
convention
美[kənˈvenʃn]
n. 習俗,慣例
evaluations
美[ɪvælj'ʊeɪʃnz]
n. 賦值
comparison
美[kəmˈpærɪsn]
n. 比較
equivalent
美[ɪˈkwɪvələnt]
adj. 相等的
2.2.6 Expanding the Bit Representation of a Number
For converting a two’s-complement number to a larger data type, the rule
is to perform a sign extension, adding copies of the most signifificant bit to the
representation, expressed by the following principle. We show the sign bit xw−1 in
blue to highlight its role in sign extension. When converting from short to unsigned
, the program first changes the size and then the type.
significant
美[sɪɡˈnɪfɪkənt]
adj. 重要的
principle
美[ˈprɪnsəpl]
n. 定律
2.2.7 Truncating Numbers
Casting x to be short will truncate a 32-bit int to a 16-bit short. As we saw
before, this 16-bit pattern is the two’s-complement representation of −12,345.
When casting this back to int, sign extension will set the high-order 16 bits to
ones, yielding the 32-bit two’s-complement representation of −12,345.
truncate
美[ˈtrʌŋkeɪt]
vt. 縮短
representation
美[ˌrɛprɪzɛnˈteʃən]
n. 表現
extension
美[ɪkˈstenʃn]
n. 延伸
本作品採用《CC 協議》,轉載必須註明作者和本文連結