D. The Omnipotent Monster Killer
題目大意:
有一棵樹,樹節點數不超過\(3·10^5\),每個節點的權值,定義為陣列\(a(a_i<10^{12})\),初始\(sum=0\),每一輪執行如下操作:
- 計算當前剩餘所有的點權和,累計到\(sum\)中
- 任選若干個互不相鄰的節點並移除
重複這個操作直到樹上沒有任何節點為止,最小化\(sum\)。
整體感覺這道題帶來的啟發很多,值得慢慢細品。
首先第一個誤區以為可以貪心的兩輪操作結束,比如:
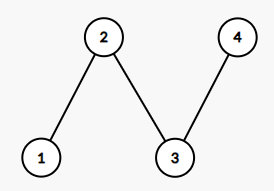
先移除2 4,再移除1 3。
但是很容易舉出反例:
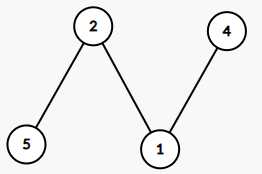
顯然要先移除4 5,再移除一個2,最後移除剩餘的1,需要三輪才能完成。
三輪能否確定結束呢?如果是鏈式結構確實是可以的,因為鏈式結構中,任意節點最多隻有兩個節點相鄰,這三者互不相同也只有三輪操作。
而在樹上,某個節點N相鄰可能有n個\(X_i\),如果每一個均在不同輪次移除,那麼節點N需要在第\(n+1\)輪才能移除。
然後是第二個誤區,是否每輪選擇樹上最大獨立集?即任選互不相鄰節點,樹形dp求權重和最大的選擇。
這個可以解決上面1-2-3-4和5-2-1-4兩種情況。
如果有多輪,似乎也可以解決,然而這也是不對的,簡單反例如下:
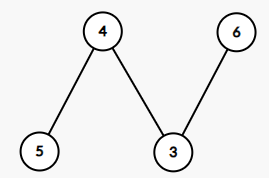
第一輪最大獨立集是(5,6),然而剩餘的(3,4)由於是相鄰的,只能先選4再選3,\(sum=(6+5+4+3)+(4+3)+3=28\)
而選擇(4,6),則有\(sum=(6+5+4+3)+(5+3)=26\)
綜上我們得出兩個結論,第一需要多輪操作才可能最小化\(sum\),第二最大獨立集的貪心思路是錯誤的。
此時一個關鍵問題擺在了我們面前,我們最多可能需要多少輪操作呢?
構造多輪的樹結構不是那麼容易,賽時也挺難悟到,這裡給出一個建樹方式
-
初始只有兩個節點1,此時我們需要一輪操作
-
新增一個節點2,此時我們需要兩輪操作
-
在1和2節點上新增4和5,此時由於我們需要先移除(4,5),所以需要三輪操作
-
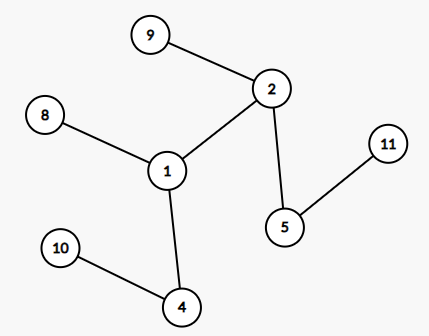
下面是遞推的構造,在之前出現的所有節點上,新增(8-11),此時第一輪移除(8-11)是最優的,加上之前的三輪,我們就需要四輪操作
-
...重複下去,每輪新增的節點個數是\(2^{x-2}\),節點權值分別是\([2^{x-1},2^{x-1}+2^{x-2}-1]\)。
這樣需要x輪操作移除所有節點的情況下,節點總數需要\(2^{x-1}\),而節點總數是\(n\)的情況下,我們至多需要的輪數就是\(logn+1\)
這是第一個難點,需要能推算到至多需要的輪數是\(logn+1\) 不妨設\(T=logn+1\)
討論真正的做法前,我們需要反思以下:
之前常做的樹形dp往往是對一個節點的操作是選或者不選這種兩個狀態的轉移,典型就是樹的最大獨立集。
就算是多節點多狀態也往往是題意裡推匯出的帶有意義的固定個數,比如968. 監控二叉樹
這導致很容易把樹形dp中dp的內涵忽略,對本題而言,雖然是樹形dp,但是節點卻是有\(T=logn+1\)這樣一個狀態數。
因此第二個難點就是,要能發現樹形dp的狀態需要定義為陣列\(dp[i][j]\),其中\(i\)為節點,\(j∈[1,T]\)。每個節點可能出現在任何一輪,而如果節點在第x輪移除,那麼他產生的對\(sum\)的貢獻為\(x*a_i\)。
然後如何進行狀態轉移呢?每個節點需要基於所有子節點的狀態進行轉移
這是難點三,推導轉移方程。每個節點的初始都是一致的,即每輪的自身代價。
這裡假設節點i有k個子節點,轉移中,是對於每個自身輪數,需要依次累加子節點不同輪數的最小\(sum\)
即\(f[i][j]= dp[i][j] + \sum_{s=1}^k(min(f[s][t]),(t∈[1,T],t≠j))\)
簡單列舉每個\(j∈[1,T]\),再列舉子節點\(t∈[1,T]\),取\(j≠t\)的最小值,複雜度為\(O(log^2n)\)
整體複雜度\(O(nlog^2n)\)
不過這裡有個經典小技巧用於處理這個問題。
對於每個\(t∈[1,T]\),可以遍歷依次統計\(dp[s][t]\)的最小值min和次小值min2
然後對於每個\(j\),則有
所以整體複雜度可以降為\(O(nlogn)\)
核心程式碼如下(未使用該技巧,本題沒卡log)
long[][] f = new long[n][];
for(int i = 0; i < n; i++) f[i] = new long[T];
void DFS(int u, int fa)
{
for(int k = 0; k < T; k++)
{
f[u][k] = (k + 1) * w[u];
}
foreach(int v in g[u])
{
if(v == fa) continue;
DFS(v, u);
for(int k = 0; k < T; k++)
{
long min = long.MaxValue;
for(int s = 0; s < T; s++)
{
if(s != k) min = Math.Min(min, f[v][s]);
}
f[u][k] += min;
}
}
}
DFS(0, -1);
long ans = long.MaxValue;
for(int i = 0; i < T; i++) ans = Math.Min(f[0][i], ans);
Print(ans);