前言
喵喵於 \(2024.3.18\) 建立 \(vjudge\) 團隊 \(NOIP2024\) ,成員為全體 \(HZOI2024\) 初三現役人員,旗下三個板塊的專題訓練,分別為動態規劃、圖論、字串,其中題目非紫即黑,存在少量藍。
並於 \(2024.3.19\) 成功關閉 \(luogu\) 。
-
團隊連結
-
動態規劃
-
圖論
-
字串
接下來做的題我會按照開題順序(大抵等同於從易到難)將 \(A\) 掉的題記錄下來,同時可能有類似題的擴充套件。
動態規劃專題
B - Birds
- \(3.19\) 。
混合揹包 \(DP\) 。
定義 \(f_{i,j}\) 表示取到鳥巢 \(i\) ,獲得 \(j\) 只小鳥時所剩的魔力值。
顯然有 \(f_{0,0}=1\) 。
轉移為:
其中 \(k\) 表示對於鳥巢 \(i\) 取了幾個鳥,其餘變數意義與上述表達或題面相同。
特別的,有任意 \(f_{i+1,j+k}\leq w+(j+k)\times b\) ,又題意可得。
注意:
-
將所有 \(f_{i,j}\) 初始化為 \(-1\) (表示沒有更新過,而 \(0\) 可能是恰好為 \(0\) 並非未更新,會產生歧義),若 \(f_{i,j}\) 沒有更新過,即他此時所剩魔力值 \(<0\) ,則無法更新 \(f_{i+1,j+k}\) 。
-
若 \(f_{i,j}-k\times cost_i<0\) 說明無法取這麼多鳥,那麼顯然更大的 \(k\) 也無法取到,所以 \(break\) 。
-
對於 \(j\) 應迴圈到 \(sum_i\) ,\(sum_i\) 表示 \(c_i\) 的字首和,即最多取這麼多鳥。
同理的,\(k\) 迴圈到 \(c_i\) 。
當然,\(j,k\) 均從 \(0\) 開始迴圈。
最後處理答案,顯然我們取完鳥巢 \(n\) 後的答案將體現在 \(f_{n+1,j}\) 中,答案為所有 \(\geq 0\) 的 \(f_{n+1,j}\) 中 \(j\) 的最大值。
點選檢視程式碼
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N=1e3+10,M=1e4+10;
template<typename Tp> inline void read(Tp&x)
{
x=0;register bool z=true;
register char c=getchar();
for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0;
for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
x=(z?x:~x+1);
}
int n,w,b,x,ans,c[N],v[N],sum[N],f[N][M];
signed main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
read(n),read(w),read(b),read(x);
for(int i=1;i<=n;i++)
read(c[i]),
sum[i]=sum[i-1]+c[i];
for(int i=1;i<=n;i++) read(v[i]);
memset(f,-1,sizeof(f));
f[0][0]=w;
for(int i=0;i<=n;i++)
for(int j=0;j<=sum[i];j++)
for(int k=0;k<=c[i];k++)
{
int s=f[i][j];
if(s<0) break;
s-=k*v[i];
if(s<0) break;
s=min(s+x,w+(j+k)*b);
f[i+1][j+k]=max(f[i+1][j+k],s);
}
for(int i=0;i<=sum[n];i++)
if(f[n+1][i]>=0)
ans=max(ans,i);
cout<<ans;
}
I - Game on Sum (Easy Version)
- \(3.20\) 。
此題為簡單版,可以直接跑 \(DP\) 。
定義 \(f_{i,j}\) 表示進行了 \(i\) 輪,其中 \(Bob\) 選擇加的有 \(j\) 輪時的分數。
設 \(x_i\) 表示 \(Alice\) 本輪選擇的數。
-
若選擇加,則有本輪分數為 \(f_{i-1,j-1}+x_i\) 。
-
若選擇減,則有本輪分數為 \(f_{i-1,j}-x_i\) 。
顯然 \(Bob\) 會選擇 \(\min(f_{i-1,j-1}+x_i,f_{i-1,j}-x_i)\) 。
已知兩者相加為定值,那麼顯然當兩者相等時,\(\min(f_{i-1,j-1}+x_i,f_{i-1,j}-x_i)\) 最大。
所以 \(Alice\) 會選擇兩者相等時的情況,則有:
同時,顯然有 \(f_{i,0}=0\) ,\(f_{i,i}=i\times k\) 。
最後答案為 \(f_{n,m}\) 。
點選檢視程式碼
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N=2010,P=1e9+7;
template<typename Tp> inline void read(Tp&x)
{
x=0;register bool z=true;
register char c=getchar();
for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0;
for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
x=(z?x:~x+1);
}
int t,n,m,k,f[N][N],inv2;
int qpow(int a,int b)
{
int ans=1;
for(;b;b>>=1)
{
if(b&1) (ans*=a)%=P;
(a*=a)%=P;
}
return ans;
}
signed main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
read(t);
inv2=qpow(2,P-2);
while(t--)
{
read(n),read(m),read(k);
for(int i=1;i<=n;i++)
for(int j=0;j<=min(i,m);j++)
if(i==j) f[i][j]=(k*i)%P;
else if(j==0) f[i][j]=0;
else f[i][j]=(((f[i-1][j]+f[i-1][j-1])%P)*inv2)%P;
cout<<f[n][m]<<endl;
}
}
Game on Sum (Hard Version)
- \(3.20\) 。
此題為困難版,將 \(n,m,t\) 的範圍都大大增加,無法跑正常的 \(DP\) 。
所以去思考上面所述 \(DP\) 中關於答案的貢獻。
不難發現,上述 \(DP\) 可以組成一個類似於楊輝三角的東西。
去考慮 \(f_{i,i}\) 對於答案的貢獻,因為只有 \(f_{i,i}\) 在跑 \(DP\) 之前是確定的。
我們發現對於 \(f_{i,j}\) ,他將對 \(f_{i+1,j}\) 與 \(f_{i+1.j+1}\) 產生 \(1\) 的貢獻( \(1\) 指 $1\times $ 自身)。
那麼以此類推,\(f_{i,i}\) 將對 \(f_{n,m}\) 產生 \(n-i\) 的貢獻,其中選擇 \(m-i\) 去加。
但同時如果從 \(f_{i,i}\) 去考慮的話,他還會給 \(f_{i+1,i+1}\) 產生 \(1\) 的貢獻,但這裡已經填好了,所以直接從 \(f_{i+1,i}\) 開始考慮即可,從 \(f_{i+1,i}\) 到 \(f_{n,m}\) 要對 \(n\) 產生 \(n-i-1\) 次貢獻,從中選擇 \(m-i\) 次對 \(m\) 產生貢獻。
也就是 \(f_{i,i}\) 對 \(f_{n,m}\) 的貢獻為 \(\dfrac{i\times k\times \text{C}_{n-i-1}^{m-i}}{2^{n-i}}\) 。
這個 \(2^{n-i}\) 顯然,每次都是要 \(÷2\) 的,而 \(i\times k\) 表示 \(f_{i,i}\) 自身。
由此最後的答案就為:
至於只迴圈到 \(m\) ,因為 \(Bob\) 只會選擇 \(m\) 輪去加。
關於程式碼:首先需要預處理階乘與每個 \(2^i\),乘法逆元可用費馬小定理 \(+\) 快速冪,因為預處理需要到 \(1e9\) 顯然會炸。
點選檢視程式碼
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N=1e6+10,P=1e9+7;
template<typename Tp> inline void read(Tp&x)
{
x=0;register bool z=true;
register char c=getchar();
for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0;
for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
x=(z?x:~x+1);
}
int t,n,m,k,jc[N],inv2[N];
int qpow(int a,int b)
{
int ans=1;
for(;b;b>>=1)
{
if(b&1) (ans*=a)%=P;
(a*=a)%=P;
}
return ans;
}
void pre()
{
jc[0]=jc[1]=1;
for(int i=2;i<=N-1;i++) jc[i]=(jc[i-1]*i)%P;
inv2[0]=1,inv2[1]=2;
for(int i=2;i<=N-1;i++) inv2[i]=(inv2[i-1]*2)%P;
}
int C(int m,int n)
{
if(m==0||n==m) return 1;
return (((jc[n]*qpow(jc[m],P-2))%P)*qpow(jc[n-m],P-2))%P;
}
signed main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
pre();
read(t);
while(t--)
{
read(n),read(m),read(k);
if(n==m)
{
cout<<(n*k)%P<<endl;
continue;
}
int ans=0;
for(int i=1;i<=m;i++)
(ans+=(((((i*k)%P)*C(m-i,n-i-1))%P)*qpow(inv2[n-i],P-2))%P)%=P;
cout<<ans<<endl;
}
}
切切糕
-
\(3.21\) 。
-
多倍經驗。
這個乏味範圍是小的,\(DP\) 即可。
貪心思想,\(Tinytree\) 會將優先權給儘可能大的糕,所以將 \(a_i\) 從大到小排序。
當其擁有優先權時,設 \(Kiana\) 會將 \(a_i\) 分成 \(x_i\) 與 \(a_i-x_i\) ,那麼顯然 \(Tinytree\) 會將 \(\min(x_i,a_i-x_i)\) 給 \(Kiana\) 。
定義 \(f_{i,j}\) 是 \(Kiana\) 在分完第 \(i\) 塊,其中 \(Tinytree\) 用了 \(j\) 次優先權時分到的蛋糕大小。
與上面類似的,使 \(\min(f_{i,j-1}+x_i,f_{i,j}+a_i-x_i)\) 最大,有:
最後答案為 \(sum-f_{n,m}\) ,\(sum\) 指 \(\sum\limits_{i=1}^na_i\) 。
點選檢視程式碼
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N=2510;
const double eps=1e-12;
template<typename Tp> inline void read(Tp&x)
{
x=0;register bool z=true;
register char c=getchar();
for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0;
for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
x=(z?x:~x+1);
}
int n,m;
double a[N],sum[N],f[N][N];
bool cmp(double a,double b) {return a-b>eps;}
signed main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
read(n),read(m);
for(int i=1;i<=n;i++) cin>>a[i];
stable_sort(a+1,a+1+n,cmp);
for(int i=1;i<=n;i++) sum[i]=sum[i-1]+a[i];
for(int i=1;i<=n;i++)
for(int j=0;j<=min(i,m);j++)
if(j==0) f[i][j]=0;
else if(i==j) f[i][j]=sum[i]/2.0;
else f[i][j]=max((f[i-1][j-1]+f[i-1][j]+a[i])/2.0,f[i-1][j]);
printf("%.6f",sum[n]-f[n][m]);
}
A - Helping People
-
\(3.24\)
主要是 \(3.21\) 打的,當時由於某些紙張問題沒調出來,而中間經歷了 \(whk\) 考試與放假,所以相隔了 \(3\) 天。
樹形 \(DP\) ,機率 \(DP\) 。
首先我們需要明確他問的是啥:
-
“好處”:所有人擁有的金額中的最大值。
-
“期望”:從期望的本質去想 ,其意義為 \(\sum\limits_{i=1}^nq_ix_i\) ,也就是每個最大指乘上他的機率再加一起。
可見他問的是最大值的期望,並非期望的最大值。
我們發現他每個區間要麼包含要麼不相交,所以可以將其轉化為一個樹的結構去跑樹形 \(DP\) ,類似於線段樹的一個結構,每個節點表示一個區間。
當然他可能是個森林,所以再加一個 \([1,n]\) 的區間,對應機率為 \(0\) 的節點作為根節點。
那麼我們將他按照區間長度從大到小排序,就可以簡單的簡稱一棵樹。
定義 \(a_i\) 為第 \(i\) 個人的初始值,對於區間 \(i\) 中 \(a\) 的最大值 為 \(mx_i\) 。不難發現這個區間最後的最大值 \(\in {mx_i\sim mx_i+m}\) 。
那麼我們定義 \(f_{i,j}\) 為對於區間 \(i\) 的最大值 \(\leq mx_i+j\) 時的機率,對此有轉移方程:
最後答案為 \(\sum\limits_{i=0}^m(f_{1,i}-f_{1,i-1})\times (i+mx_1)\) ,因為顯然第 \(1\) 個區間為 \([1,n]\) 。當然 \(0\) 要特判。
點選檢視程式碼
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N=1e5+10,M=5010;
template<typename Tp> inline void read(Tp&x)
{
x=0;register bool z=true;
register char c=getchar();
for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0;
for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
x=(z?x:~x+1);
}
int n,m,mx[N][20];
double ans,f[M][M];
vector<int>son[N];
struct aa
{
int l,r,mx;
double p;
}e[M];
bool cmp(aa a,aa b) {return a.r-a.l>b.r-b.l;}
void init()
{
for(int j=1;j<=log2(n);j++)
for(int i=1;i<=n-(1<<j)+1;i++)
mx[i][j]=max(mx[i][j-1],mx[i+(1<<(j-1))][j-1]);
}
int ask(int l,int r)
{
int t=log2(r-l+1);
return max(mx[l][t],mx[r-(1<<t)+1][t]);
}
void build()
{
stable_sort(e+1,e+1+m,cmp);
for(int i=1;i<=m;i++)
for(int j=i-1;j>=1;j--)
if(e[j].l<=e[i].l&&e[j].r>=e[i].r)
{
son[j].push_back(i);
break;
}
}
void dfs(int i)
{
f[i][0]=1-e[i].p;
for(int j:son[i])
dfs(j),
f[i][0]*=f[j][min(m,e[i].mx-e[j].mx)];
for(int k=1;k<=m;k++)
{
double sum1=1,sum2=1;
for(int j:son[i])
sum1*=f[j][min(m,k-e[j].mx+e[i].mx-1)],
sum2*=f[j][min(m,k-e[j].mx+e[i].mx)];
f[i][k]=e[i].p*sum1+(1-e[i].p)*sum2;
}
}
signed main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
read(n),read(m);
for(int i=1;i<=n;i++)
read(mx[i][0]);
init();
for(int i=1;i<=m;i++)
read(e[i].l),read(e[i].r),
cin>>e[i].p,
e[i].mx=ask(e[i].l,e[i].r);
e[++m].l=1,e[m].r=n,e[m].p=0,e[m].mx=ask(1,n);
build();
dfs(1);
for(int i=0;i<=m;i++)
ans+=(f[1][i]-(i==0?0:f[1][i-1]))*(i+e[1].mx);
printf("%.9f",ans);
}
C - Positions in Permutations
- \(3.26\)
\(DP+\) 容斥 \(+\) 組合計數
定義 \(f_{i,j,k,l}\) 為前 \(i\) 個數中有 \(j\) 個是好的,第 \(i\) 位和第 \(i+1\) 位被佔用情況分別為 \(l,k\) (布林)。
去思考轉移方程,有:
按照 \(i-1,i,i+1\) 是否被選分別考慮即可,其中後兩個因為選了 \(i+1\) 所以一定多了一個“好的”,就只有 \(j-1\) 的情況。
那麼所有排列中至少有 \(i\) 個是“好的”的方案數就是 \(ans_i=(f_{n,i,1,0}+f_{n,i,0,0})\times (n-i)!\)
於是發現需要容斥。
思考 \(f_{n,i}\) 的貢獻為 \(\text{C}_i^m\times ans_i\) (\(m\leq i\leq n\)),於是透過容斥,有:
點選檢視程式碼
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
const int N=1010,P=1e9+7;
template<typename Tp> inline void read(Tp&x)
{
x=0;register bool z=true;
register char c=getchar();
for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0;
for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
x=(z?x:~x+1);
}
int n,m,f[N][N][2][2],jc[N],anss,ans[N],C[N];
int qpow(int a,int b)
{
int ans=1;
for(;b;b>>=1)
{
if(b&1) (ans*=a)%=P;
(a*=a)%=P;
}
return ans;
}
void pre()
{
jc[0]=jc[1]=1;
for(int i=2;i<=N-1;i++)
jc[i]=(jc[i-1]*i)%P;
C[m]=1;
for(int i=m+1;i<=n;i++)
C[i]=(((C[i-1]*i)%P)*qpow(i-m,P-2))%P;
}
signed main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
read(n),read(m);
pre();
f[1][1][0][1]=f[1][0][0][0]=1;
for(int i=2;i<=n;i++)
for(int j=0;j<=i;j++)
{
(f[i][j][0][0]+=f[i-1][j][1][0]+f[i-1][j][0][0])%=P;
if(j) (f[i][j][0][0]+=f[i-1][j-1][0][0])%=P;
(f[i][j][1][0]+=f[i-1][j][0][1]+f[i-1][j][1][1])%=P;
if(j) (f[i][j][1][0]+=f[i-1][j-1][0][1])%=P;
if(i!=n&&j)
(f[i][j][0][1]+=f[i-1][j-1][0][0]+f[i-1][j-1][1][0])%=P,
(f[i][j][1][1]+=f[i-1][j-1][0][1]+f[i-1][j-1][1][1])%=P;
}
for(int i=m;i<=n;i++)
ans[i]=(((f[n][i][1][0]+f[n][i][0][0])%P)*jc[n-i])%P;
for(int i=m,t=0;i<=n;i++,t++)
(anss+=(((qpow(-1,t)*C[i])%P)*ans[i])%P+P)%=P;
cout<<anss;
}
F - ZS Shuffles Cards
-
\(3.30\)
前幾天去調模擬賽和分塊了。
感覺挺水的,為啥評 \(3000\) ,\(luogu\) 上都降紫了,
個人感覺比 \(A\) 簡單多了。
機率期望 \(DP\) 。
首先如果直接跑期望 \(DP\) 的話。
\(f_i\) 表示已經取了 \(i\) 張數字牌,還需要的期望,\(f_n=0\) 。
-
\(\dfrac{n-i}{n+m-i}\) 的機率取到新的牌。
-
\(\dfrac{m}{n+m-i}\) 的機率取到
joker,此時就要從頭開始了。
那麼有:
顯然這個式子非常好想,但是發現不滿足無後效性,不能遞推實現,需要高斯消元,那麼 \(O(n^3)\) 顯然 \(TLE\) 了,而且及其難打。
所以需要轉變思路。
不放將期望分成兩個部分:
-
輪數的期望。
-
每輪所需秒數的期望。
那麼顯然這兩個東西乘起來就是最後的答案。
-
先求輪數的期望:
定義 \(f_i\) 表示還需要取 \(i\) 張數字牌,換而言之就是已經取了 \(n-i\) 張數字牌時還需要的輪數的期望。
有 \(f_0=1\) ,因為當所有數字牌都取完時,根據題意,還需要再取到一張
joker才能結束,剩下的牌顯然都是joker了,所以還需要 \(1\) 輪。發現是正著跑的,並非通常的倒著跑,其實沒有太大的區別,
只是這麼寫的話程式碼能少打幾個字,仔細想的話,已經取了 \(i\) 張數字牌和還需要 \(i\) 張數字牌沒有本質的區別。那麼轉移方程也非常好想:
\[f_i=\dfrac{i}{m+i}\times f_{i-1}+\dfrac{m}{m+i}\times (f_i+1) \]化簡為:
\[f_i=f_{i-1}+\dfrac{m}{i} \]解釋一下:
-
\(\dfrac{i}{m+i}\) 的機率取到新的牌。
-
\(\dfrac{m}{m+i}\) 的機率取到
joker,顯然就需要開啟新的一輪了。
-
-
每輪所需秒數的期望:
-
第一種理解方法:
我們發現取到的是哪一個數字牌不重要,重要的是取到的是數字牌。
那麼不放將這一堆數字牌看做一個,那麼在取到
joker前一個取到數字牌的機率就為 \(\dfrac{1}{m+1}\) 。不難發現該式子表示的就是對於每一個數字牌,在他後面開啟新的一輪的機率。
思考期望的定義:\(\sum\limits_{i=1}^nq_i\times x_i\) ,每一張牌他對秒數的貢獻都為 \(1\) ,而在他後面開啟新的一輪的機率為 \(\dfrac{1}{m+1}\) 。
那麼有每輪的秒數期望值 \(=1+\sum\limits_{i=1}^n 1 \times \dfrac{1}{m+1}=1+\dfrac{n}{m+1}\) ,至於為什麼 \(+1\) ,取到
joker也算一秒。 -
第二種理解方法:
我們知道如果對於這一秒他開啟新的一局的機率為 \(\dfrac{1}{a}\) ,那麼他這一局進行的秒數的期望就為 \(a\) 。
那麼對於這個場景,我們設他在第 \(i\) 秒結束,在第 \(i\) 秒時他取到
joker的機率為 \(\dfrac{m}{n+m-(i-1)}\) ,那麼取他的倒數,有:\[i=\dfrac{n+m-(i-1)}{m} \]解這個方程,有 \(i=\dfrac{n+m+1}{m+1}=1+\dfrac{n}{m+1}\) 。
-
最後答案就為 \(f_n\times (1+\dfrac{n}{m+1})\) 。
點選檢視程式碼
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
#define sort stable_sort
using namespace std;
const int N=4e6+10,P=998244353;
template<typename Tp> inline void read(Tp&x)
{
x=0;register bool z=true;
register char c=getchar();
for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0;
for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
x=(z?x:~x+1);
}
void wt(int x){if(x>9)wt(x/10);putchar((x%10)+'0');}
void write(int x){if(x<0)putchar('-'),x=~x+1;wt(x);}
int n,m,f[N];
int qpow(int a,int b)
{
int ans=1;
for(;b;b>>=1)
{
if(b&1) (ans*=a)%=P;
(a*=a)%=P;
}
return ans;
}
signed main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
read(n),read(m);
f[0]=1;
for(int i=1;i<=n;i++)
f[i]=(f[i-1]+(m*qpow(i,P-2))%P)%P;
cout<<(f[n]*(1+(n*qpow(m+1,P-2))%P)%P)%P;
}
H - Tavas in Kansas
-
\(4.1\)
周測沒和喵喵請下來假。
分別以 \(s,t\) 為起點先跑兩邊 \(dijkstra\) ,處理出其到每個點的距離 \(d_{s,i},d_{t,i}\) 。
那麼根據此我們可以知道每個點他距離 \(s,t\) 分別是第幾遠的,並將其離散化成 \(x_i,y_i\) ,由此形成一個 \(n\times n\) 矩陣。
Tavas每次取一行,Nafas每次取一列,那麼現在問題就轉化的不那麼複雜了。
我們想要知道 Tavas 和 Nafas 誰的得分高,並不需要知道其各自的具體分數,所以定義 \(f_{i,j,0/1}\) 分別表示目前 Tavas 取到第 \(i\) 行,Nafas 取到第 \(j\) 列時,Tavas 與 Nafas 的得分差,其中 \(0\) 表示輪到 Tavas 取,\(1\) 表示輪到 Nafas 取。
於是在此遇到三個問題:
-
最後答案是輪到誰的問題。
-
取過的點不能再取的問題。
-
每次必須取一個新點的問題。
一次解決這些問題:
-
最後答案輪到誰?
發現從前往後遞推,到答案時我們需要處理出輪到誰。
然而我們知道
Tavas為先手,如果從後往前跑的話,本質上不會影響答案,且知道到答案時一定是輪到Tavas,所以我們選擇從後往前遞推。 -
取過的點不能再取。
我們現在已知他取到第 \(i\) 行第 \(j\) 列,也就是說在第 \(i\) 行第 \(j\) 列之前都已經取過了。
-
那麼對於
Tavas,他可以取 \(i,j\) 到 \(i,n\) 中的點。 -
同樣對於
Nafas,她可以取 \(i,j\) 到 \(n,j\) 中的點。
問題解決。
-
-
每次都要取到新點。
根據我們上一個問題的分析,我們知道兩人本次活動取什麼範圍內的點。
首先該範圍內的點一定是沒有取過的。
那麼如果該範圍存在點,接等同於存在新點,於是可以轉移。
不妨用一個新的變數處理每個範圍內有幾個點。
上面所說的一些均可以用二維字首和維護。
轉移方程:
因為我們 \(f\) 表示的是 Tavas 得分與 Nafas 得分的差,所以 Tavas 希望差儘可能大,Nafas 希望得分儘可能小。
其中 \(sum1(x1,y1,x2,y2)\) 表示從 \(x1,y1\) 到 \(x2,y2\) 這一範圍內權值和,\(sum2(x1,y1,x2,y2)\) 表示 \(x1,y1\) 到 \(x2,y2\) 這一範圍點的個數。
最後根據 \(f_{1,1,0}\) 的正負輸出答案即可。
點選檢視程式碼
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
#define sort stable_sort
using namespace std;
const int N=2010,M=2e5+10;
template<typename Tp> inline void read(Tp&x)
{
x=0;register bool z=true;
register char c=getchar();
for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0;
for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
x=(z?x:~x+1);
}
int n,m,s,t,p[N],x[N],y[N],d[N],dis[N],a[N][N],b[N][N],sum1[N][N],sum2[N][N],f[N][N][2];
bool v[N];
int head[N],to[M],w[M],nxt[M],tot;
void add(int x,int y,int z)
{
nxt[++tot]=head[x];
to[tot]=y;
w[tot]=z;
head[x]=tot;
}
void dijkstra(int s,int a[])
{
memset(d,0x3f,sizeof(d));
memset(v,0,sizeof(v));
priority_queue<pair<int,int>>q;
d[s]=0;
q.push(make_pair(0,s));
while(!q.empty())
{
int u=q.top().second;
q.pop();
if(!v[u])
{
v[u]=1;
for(int i=head[u];i;i=nxt[i])
{
int v=to[i],z=w[i];
if(d[v]>d[u]+z)
d[v]=d[u]+z,
q.push(make_pair(-d[v],v));
}
}
}
for(int i=1;i<=n;i++)
dis[i]=d[i];
sort(dis+1,dis+1+n);
dis[0]=unique(dis+1,dis+1+n)-(dis+1);
for(int i=1;i<=n;i++)
a[i]=lower_bound(dis+1,dis+1+dis[0],d[i])-dis;
}
int ask(int x,int y,int xx,int yy,int sum[N][N])
{
return sum[xx][yy]-sum[x-1][yy]-sum[xx][y-1]+sum[x-1][y-1];
}
signed main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
read(n),read(m),read(s),read(t);
for(int i=1;i<=n;i++) read(p[i]);
for(int i=1,u,v,z;i<=m;i++)
read(u),read(v),read(z),
add(u,v,z),
add(v,u,z);
dijkstra(s,x),dijkstra(t,y);
for(int i=1;i<=n;i++)
a[x[i]][y[i]]+=p[i],
b[x[i]][y[i]]++;
for(int i=1;i<=n+1;i++)
for(int j=1;j<=n+1;j++)
sum1[i][j]=sum1[i-1][j]+sum1[i][j-1]-sum1[i-1][j-1]+a[i][j],
sum2[i][j]=sum2[i-1][j]+sum2[i][j-1]-sum2[i-1][j-1]+b[i][j];
for(int i=n+1;i>=1;i--)
for(int j=n+1;j>=1;j--)
if(i!=n+1||j!=n+1)
f[i][j][0]=(ask(i,j,i,n,sum2)==0)?f[i+1][j][0]:max(f[i+1][j][0],f[i+1][j][1])+ask(i,j,i,n,sum1),
f[i][j][1]=(ask(i,j,n,j,sum2)==0)?f[i][j+1][1]:min(f[i][j+1][0],f[i][j+1][1])-ask(i,j,n,j,sum1);
if(f[1][1][0]<0) puts("Cry");
if(f[1][1][0]==0) puts("Flowers");
if(f[1][1][0]>0) puts("Break a heart");
}
E - Bear and Cavalry
-
\(4.1\)
關於大多數人都只做了五六道時就把所有題都講了這件事。
不出意外明天就要開字串了。
結論題。
首先如果不考慮限制的話,將 \(w_i,h_i\) 都從小到大排序,顯然有答案為 \(\sum\limits_{i=1}^nw_ih_i\) 。
接下來考慮不能騎自己馬怎麼搞。
結論:滿足限制的匹配單元僅有以下 \(4\) 種:
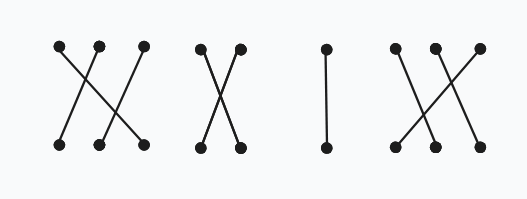
先從 \(n=3\) 開始分析:
定義 \(ban_i\) 表示 \(i\) 的馬。
-
\(ban_1\neq 1,ban_2\neq 2,ban3\neq 3。\)

-
\(ban_1\neq 1,ban_2=2,ban_3=3。\)
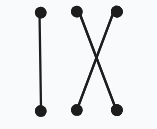
-
\(ban_1=1,ban_2=2,ban_3=3。\)
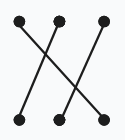
或
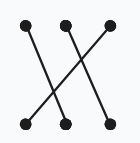
以此類以的分析,當 \(n>3\) 時,也只會產生上述 \(4\) 種匹配單元。
那麼對於每次修改,至多對左右兩邊三個產生影響,有:
如果暴力修改的話,發現會 \(TLE\) ,但是隻 \(TLE\) 一點點,發現時限是 \(3000ms\) ,我們不卡常都對不起這個 \(3000ms\) 。
發現因為在轉移時用了多個 \(if\) ,不放在每次轉移前先將其 \(w_ih_i\) (以此類推)處理出來,能少好多 \(if\) 。
於是我們就能勉強透過此題,\(3000ms\) 的時限用了 \(2700ms\) ,甚至因為評測姬波動有時候還會 \(TLE\) ,不過沒關係,多交幾遍就 \(AC\) 了。
顯然我們是卡常過的,並非正解。
所以負責任的將正解的題解放在這裡:\(@wang54321\)的題解 。
懶得打正解了。
點選檢視程式碼
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
#define sort stable_sort
using namespace std;
const int N=3e5+10;
template<typename Tp> inline void read(Tp&x)
{
x=0;register bool z=true;
register char c=getchar();
for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0;
for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
x=(z?x:~x+1);
}
int n,m,posa[N],posb[N],ban[N],w[N][4],f[N];
struct aa
{
int w,id;
}a[N],b[N];
bool cmp(aa a,aa b) {return a.w<b.w;}
signed main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
read(n),read(m);
for(int i=1;i<=n;i++)
read(a[i].w),
a[i].id=i;
for(int i=1;i<=n;i++)
read(b[i].w),
b[i].id=i;
sort(a+1,a+1+n,cmp),sort(b+1,b+1+n,cmp);
for(int i=1;i<=n;i++)
posa[a[i].id]=posb[b[i].id]=i;
for(int i=1;i<=n;i++)
ban[i]=posb[a[i].id];
for(int i=1;i<=n;i++)
{
w[i][1]=-0x3f3f3f3f;
if(i-1>=0&&ban[i]!=i)
w[i][1]=max(w[i][1],a[i].w*b[i].w);
if(i-2>=0&&ban[i]!=i-1&&ban[i-1]!=i)
w[i][2]=max(w[i][2],a[i].w*b[i-1].w+a[i-1].w*b[i].w);
if(i-3>=0&&ban[i]!=i-2&&ban[i-1]!=i&&ban[i-2]!=i-1)
w[i][3]=max(w[i][3],a[i].w*b[i-2].w+a[i-1].w*b[i].w+a[i-2].w*b[i-1].w);
if(i-3>=0&&ban[i]!=i-1&&ban[i-1]!=i-2&&ban[i-2]!=i)
w[i][3]=max(w[i][3],a[i].w*b[i-1].w+a[i-1].w*b[i-2].w+a[i-2].w*b[i].w);
}
for(int x,y,l,r;m;m--)
{
read(x),read(y);
swap(ban[posa[x]],ban[posa[y]]);
l=max(1ll,posa[x]-3),r=min(n,posa[x]+3);
for(int i=l;i<=r;i++)
{
w[i][1]=w[i][2]=w[i][3]=-0x3f3f3f3f;
if(i-1>=0&&ban[i]!=i)
w[i][1]=max(w[i][1],a[i].w*b[i].w);
if(i-2>=0&&ban[i]!=i-1&&ban[i-1]!=i)
w[i][2]=max(w[i][2],a[i].w*b[i-1].w+a[i-1].w*b[i].w);
if(i-3>=0&&ban[i]!=i-2&&ban[i-1]!=i&&ban[i-2]!=i-1)
w[i][3]=max(w[i][3],a[i].w*b[i-2].w+a[i-1].w*b[i].w+a[i-2].w*b[i-1].w);
if(i-3>=0&&ban[i]!=i-1&&ban[i-1]!=i-2&&ban[i-2]!=i)
w[i][3]=max(w[i][3],a[i].w*b[i-1].w+a[i-1].w*b[i-2].w+a[i-2].w*b[i].w);
}
l=max(1ll,posa[y]-3),r=min(n,posa[y]+3);
for(int i=l;i<=r;i++)
{
w[i][1]=w[i][2]=w[i][3]=-0x3f3f3f3f;
if(i-1>=0&&ban[i]!=i)
w[i][1]=max(w[i][1],a[i].w*b[i].w);
if(i-2>=0&&ban[i]!=i-1&&ban[i-1]!=i)
w[i][2]=max(w[i][2],a[i].w*b[i-1].w+a[i-1].w*b[i].w);
if(i-3>=0&&ban[i]!=i-2&&ban[i-1]!=i&&ban[i-2]!=i-1)
w[i][3]=max(w[i][3],a[i].w*b[i-2].w+a[i-1].w*b[i].w+a[i-2].w*b[i-1].w);
if(i-3>=0&&ban[i]!=i-1&&ban[i-1]!=i-2&&ban[i-2]!=i)
w[i][3]=max(w[i][3],a[i].w*b[i-1].w+a[i-1].w*b[i-2].w+a[i-2].w*b[i].w);
}
f[0]=0;
for(int i=1;i<=n;i++)
{
if(i-1>=0)
f[i]=f[i-1]+w[i][1];
if(i-2>=0)
f[i]=max(f[i],f[i-2]+w[i][2]);
if(i-3>=0)
f[i]=max(f[i],f[i-3]+w[i][3]);
}
cout<<f[n]<<endl;
}
}
總結
動態規劃專題到這兒就結束了,雖然還有 \(D,G\) 兩道題設計未學過知識點的題沒有做,實際上這個專題最早開還是有原因的,畢竟這東西涉及未學過知識點最少,且主要是鍛鍊思維,之前應該是從來沒有做過這樣難度的 \(DP\) ,同時儘可能的鍛鍊獨立思考能力,能不 \(hè\) 堅決不 \(hè\) ,在這裡入門晚、過知識點太倉促的缺陷也體現出來了,需要在今後的學習中努力彌補。
字串專題
前言
沒學過的知識點太多了,感覺 \(NOIP\) 題單不小心把 \(P\) 去了的感覺,後續開題的話有幾道現學知識可做的,差不多就後續開題了。
I - Minimax
- \(4.2\) 。
構造、思路題。
首先,明確 \(proper\) 字首是什麼意思。
分析題面可得,這東西和 \(kmp\) 求出來的 \(next\) 陣列是一個東西。
- \(kmp\) 學習筆記 。
首先此題 \(CF\) 評了 \(2100\) ,所以自然不是什麼高階演算法,暴力構造就好了。
思考幾種情況:
-
所有字母出現次數均為 \(1\) :
按照最小字典序輸出即可。
-
\(eg\) :
vkcup。\(ans\) :
ckpuv。
-
-
僅出現過一種字母:
輸出原字元即可。
-
\(eg\) :
zzzzzz。\(ans\) :
zzzzzz。
-
-
若有一種字母僅出現過一次:
將這個字母放在最前面,剩下的按照字典序輸出。
-
\(eg\) :
aaabccc。\(ans\) :
baaaccc。
解釋:該字母僅有一個,那麼將他放在最前面後面一定沒有字母能與其匹配,從而使 \(f(t)=0\) 。
-
-
每個字母出現次數均 \(\geq 2\) :
為了方便,我們設
a為字典序最小的字母,b為字典序第二小的字母,c作為字典序第三小的字母,\(num_i\) 為字母 \(i\) 出現的次數,\(n\) 為字串長度。首先明確,在此情況下無論如何,均可以使 \(f(t)=1\) ,很好理解的。
-
最前面可以放
aa:-
\(eg\) :
abababa。\(ans\) :
aababab。
首先這種情況的條件為 \(num_a-2\leq n-sum_a\) 。
因為首位放了
aa,為了使 \(f(t)=1\) ,後面一定不能存在連續的aa,所以一定要有 \(n-sum\) 個其他字母將 \(num_a-1\) 個 \(a\) 隔開。這種情況的構造方式就是在除首位外其餘地方不可出現連續的
aa的字典序最小情況。 -
-
最前面不可以放
aa:也就是 \(num_a-2>n-sum_a\) 的情況,此情況亦分為兩種情況:
-
僅有 \(2\) 種不同的字母:
-
\(eg\) :
aaababaabaaaa。\(ans\) :
abbbaaaaaaaaa。
即先輸出一個
a,然後將b全部輸出,再將剩餘的a全部輸出。解釋:在此情況下,顯然後面不可以出現連續的
ab,於是有上述結論。 -
-
存在 \(3\) 個及以上種不同的字母:
-
\(eg\) :
aaaababaccdaaa。\(ans\) :
abaaaaaaaacbcd。
即先輸出一個
a,在輸出一個b,再將所有的a輸出,再輸出一個c,再將所有的b輸出,剩餘的按照字典序輸出。解釋:即用一個
c將ab隔開。 -
-
-
按照上述規則構造即可。
本次的程式碼比較屎,懶得最佳化了。
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
#define sort stable_sort
using namespace std;
const int N=1e5+10;
template<typename Tp> inline void read(Tp&x)
{
x=0;register bool z=true;
register char c=getchar();
for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0;
for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
x=(z?x:~x+1);
}
int t,n,num[26],sum,id,id2,abc;
string s;
bool used;
signed main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
read(t);
while(t--)
{
memset(num,0,sizeof(num));
abc=sum=used=id=id2=0;
cin>>s;
n=s.size();
for(int i=0;i<n;i++)
{
num[s[i]-'a']++;
if(num[s[i]-'a']==1) abc++;
}
if(abc==1)
{
cout<<s<<endl;
continue;
}
int flag=-1;
for(int i=0;i<26;i++)
if(num[i]==1)
{
cout<<char(i+'a');
flag=i;
break;
}
if(flag!=-1)
{
for(int i=0;i<26;i++)
if(i!=flag)
while(num[i]--)
cout<<char(i+'a');
cout<<endl;
continue;
}
for(int i=0;i<26;i++)
if(num[i])
{
id=i;
sum=num[i];
break;
}
if(sum-2<=n-sum)
{
cout<<char(id+'a')<<char(id+'a');
sum-=2;
used=1;
n-=2;
while(n--)
if(!used&&sum)
used=1,
cout<<char(id+'a'),
sum--;
else
{
used=0;
for(int i=id+1;i<26;i++)
if(num[i])
{
cout<<char(i+'a');
num[i]--;
break;
}
}
while(sum) cout<<char(id+'a'),sum--;
}
else
{
if(abc==2)
{
cout<<char(id+'a');
sum--;
for(int i=id+1;i<26;i++)
while(num[i]--)
cout<<char(i+'a');
while(sum--)
cout<<char(id+'a');
}
else
{
cout<<char(id+'a');
sum--;
for(int i=id+1;i<26;i++)
if(num[i])
{
cout<<char(i+'a');
num[i]--;
flag=i;
break;
}
while(sum--) cout<<char(id+'a');
for(int i=flag+1;i<26;i++)
if(num[i])
{
cout<<char(i+'a');
num[i]--;
break;
}
while(num[flag]--) cout<<char(flag+'a');
for(int i=flag+1;i<26;i++)
while(num[i]--)
cout<<char(i+'a');
}
}
cout<<endl;
}
}
H - Scissors
-
\(4.3\) 。
借
hangry的 \(CF\) 提交記錄……點選檢視提交記錄
\(KMP\) 已死,\(Hash\) 當立!
本來昨天就想出來怎麼做的題,今天調了一下午。
後面會說為什麼 \(KMP┏┛墓┗┓\) 。
標籤給的 暴力字串 ,Hash 可解。
用 \(Hash\) 處理出 \(pre(t,i)\) 在主串 \(s\) 最靠左匹配到的位置(此處的最左應是在 \(>k\) 的前提下),以及 \(suf(t,i)\) 在主串 \(s\) 最靠右匹配到的位置(同理在 \(<n-k+1\) 前提下),分別用 \(l_i,r_i\) 表示。
找到一組 \(l_i,r_{m-i}\) ,滿足:
時,即匹配成功。
但問題還沒有結束,若存在某一字串在主串中完整出現過,那麼他可能盡在兩端的其中一段出現過,不滿足上面的條件,所以特判即可。
思路不難,但是各種細節非常噁心(要不然我也不能調一下午)。
-
\(KMP┏┛墓┗┓\) :
我們要的 \(l_i\) 與 \(r_i\) 應儘可能靠左或靠右,但是 \(KMP\) 演算法在乎的只是將模式串儘可能的在主串中完整的匹配出來,由此他跑出來的 \(l_i,r_i\) 是錯誤的。
-
\(Hack\) :
27 11 9 bbaabababaaaabbbbabaababaab abababaabab
上述樣例用 \(KMP\) 跑他會告訴你 \(l_3=20\) ,但顯然應為 \(10\) ,因為在主串中 \(sub(4,11)\) 均是匹配成功的,他就直接從 \(12\) 開始跑了。
-
-
當模式串能整個在主串中匹配時,需要判斷的地方也很多:
我們設 \(ans\) 為他匹配到的位置。
且此時是滿足 \(m\leq k\) 的,否則還是需要拼出來。
-
\(ans-k+1\) 是否 \(\geq 1\) :
是,則輸出 \(1\) 。
-
\(ans-k+1\) 是否與 \(n-k+1\) 有重疊:
是,則輸出 \(n-k+1-k\) 。
解釋一下,右面部分從最後開始剪即可,因為左半部分已經包含全部模式串。
-
-
處理 \(l_i,r_i\) 時:
\(i\) 迴圈到 \(\min(k,m)\) ,再往後跑會出現負數導致出錯,此處看程式碼理解。
最後,\(Hack\) 資料在 \(CF\) 中十分充盈,本人演算法可能還是有漏洞,歡迎 \(Hack\) 。
讓我們為 KMP 節哀
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
#define sort stable_sort
using namespace std;
const int N=5e5+10,P=1e9+7;
template<typename Tp> inline void read(Tp&x)
{
x=0;register bool z=true;
register char c=getchar();
for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0;
for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
x=(z?x:~x+1);
}
int n,m,k,ba[N],a[N],b[N],l[N],r[N],ans;
char s[N],t[N];
void pre()
{
ba[0]=0,ba[1]=233;
for(int i=2;i<=n;i++)
ba[i]=(ba[i-1]*ba[1])%P;
}
void Hash(char s[],int x[],int len)
{
x[0]=0;
for(int i=1;i<=len;i++)
x[i]=((x[i-1]*ba[1])%P+s[i])%P;
}
int ask(int x[],int l,int r)
{
return (x[r]-x[l-1]*ba[r-l+1]%P+P)%P;
}
signed main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
read(n),read(m),read(k);
cin>>s+1>>t+1;
pre();
Hash(s,a,n),Hash(t,b,m);
for(int i=m;i<=n;i++)
if(ask(b,1,m)==ask(a,i-m+1,i))
{
ans=i;
break;
}
if(ans!=0&&m<=k)
{
puts("Yes");
if(ans-k+1<=0) cout<<1;
else if(ans>=n-k+1) cout<<n-k*2+1;
else cout<<ans-k+1;
cout<<' '<<n-k+1;
return 0;
}
if(ans!=0&&m>k)
{
puts("Yes");
cout<<max(1ll,ans-m/2-k+1)<<' '<<max(1ll,ans-m/2-k+1)+k;
return 0;
}
for(int i=1,j=k;i<=min(k,m);i++)
{
while(j<=n&&ask(b,1,i)!=ask(a,j-i+1,j))
j++;
if(ask(b,1,i)==ask(a,k-i+1,k))
j=k;
l[i]=j;
}
for(int i=1,j=n-k+1;i<=min(k,m);i++)
{
while(j>=1&&ask(b,m-i+1,m)!=ask(a,j,j+i-1))
j--;
if(ask(b,m-i+1,m)==ask(a,n-k+1,n-k+i))
j=n-k+1;
r[i]=j;
}
for(int i=1;i<=m;i++)
if(l[i]<r[m-i]&&l[i]>=k&&l[i]<=n&&r[m-i]+k-1<=n&&r[m-i]>=1)
{
puts("Yes");
cout<<l[i]-k+1<<' '<<r[m-i];
return 0;
}
puts("No");
}
G - x-prime Substrings
- \(4.4\) 。
正解是 DFS \(+\) AC自動機,但是 狀壓 DP 可解。
用 \(f_{i,sub}\) 表示列舉到第 \(i\) 個點,字首和狀態為 \(sub\) 時其後面需要刪除的最小個數。
根據定義,選擇倒序遞迴處理,同時記憶化減小時間複雜度,目標 \(f_{1,1}\) 。
可能比較難理解,一個一個解釋:
-
\(sub\) :
二進位制表示字首和狀態。
若其在 \(2^x\) 位置為 \(1\) ,表示其字首和中存在 \(x\) 。
比如一個字首能組成的和有 \(1,2,6,7,8\) ,那麼他的狀態就表示為 \(111000111\) ,其中最後一位是為 \(2^0\) ,此處沒有實際意義,但後面有用處。
-
如何更新 \(sub\) ?
繼續用上面的例子,若要將這個字首和 \(+4\) ,即將 \(sub\times 2^4+1\) ,變為 \(1110001110001\) ,發現其能組成的和就為 \(4,5,6,10,11,12\) ,級將上面的 \(1,2,6,7,8\) 均 \(+4\) ,而這個 \(4\) 就是 \(0+4\) ,這也是為什麼要保持最後一位 \(=1\) 。
-
如何判斷 \(sub\) 是否合法?
-
先判斷該 \(sub\) 是否包含 \(x\) ,即 \(2^x\) 位置是否為 \(1\) ,如果不存在,那一定是合法了。
-
如果存在 \(x\) ,再判斷其是否存在 \(x\) 的約數,若有,則仍是合法的。
但這樣顯然不正確,需要改進,不放先將 \(>x\) 的字首和全部刪去(必定合法),再將 \(>x\) 的約數的字首和全部刪去,這樣的話保證了正確性,同時減少了狀態數。
-
-
狀態轉移:
\[f_{i,sub}=\min(f_{i+1,sub}+1,f_{i+1,sub\times 2^{a_i}+1}) \]即位置 \(i\) 的數是否被選,若不選顯然需要刪除的點數 \(+1\) ,否則字首和狀態 \(+a_i\) ,\(a_i\) 為當前點表示的數。
邊界 \(f_{i,sub}=0(i>n)\) 。
目標 \(f_{1,1}\) 。
當然狀態太大陣列存不下,用 \(unordered\_map\) 即可。
\(2000ms\) 的時限跑了 \(1999ms\) ,\(\large{😅😅😅}\) 。
看似複雜度會假,實際上 \(x-prime\) 很少,勉強能過。
點選檢視程式碼
#include<bits/stdc++.h>
#define int long long
#define endl '\n'
#define sort stable_sort
using namespace std;
const int N=1010;
template<typename Tp> inline void read(Tp&x)
{
x=0;register bool z=true;
register char c=getchar();
for(;c<'0'||c>'9';c=getchar()) if(c=='-') z=0;
for(;'0'<=c&&c<='9';c=getchar()) x=(x<<1)+(x<<3)+(c^48);
x=(z?x:~x+1);
}
char s[N];
int m,n,a[N],con;
unordered_map<int,int>f[N];
void calc(int &sub)
{
sub&=((1<<m)-1);
int tmp=sub&con;
if(tmp==0) return ;
tmp&=-tmp;
sub&=(tmp-1);
}
bool check(int sub)
{
if((sub&(1<<m))==0) return 1;
if(sub&con) return 1;
return 0;
}
int dfs(int x,int sub)
{
if(x>n) return 0;
calc(sub);
if(f[x].count(sub)>0) return f[x][sub];
int lsub=sub,ans=dfs(x+1,sub)+1;
sub=(sub<<a[x])|1;
if(check(sub))
ans=min(ans,dfs(x+1,sub));
return f[x][lsub]=ans;
}
signed main()
{
#ifndef ONLINE_JUDGE
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
#endif
cin>>s+1;
read(m);
n=strlen(s+1);
for(int i=1;i<=n;i++)
a[i]=s[i]-'0';
for(int i=1;i<m;i++)
if(m%i==0)
con|=(1<<i);
cout<<dfs(1,1);
}