Codeforces Global Round 27 總結
A
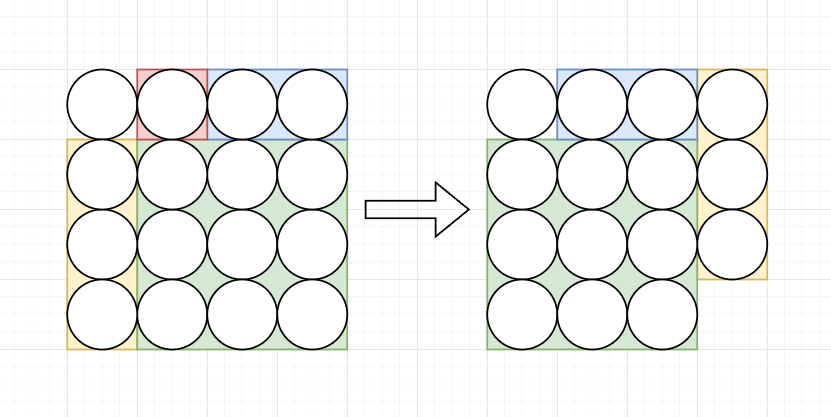
將紅色的位置 \((r,c)\) 移走,分為三塊來考慮,藍色的塊移動 \(m-c\),黃色的塊移動 \(m*(n-r)\),綠色的塊移動 \((m-1)*(n-r)\)。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
#include <queue>
#include <map>
using namespace std;
typedef long long ll;
const int N=1;
ll n,m,r,c;
void solve()
{
cin>>n>>m>>r>>c;
cout<<m-c+m*(n-r)+(m-1)*(n-r)<<'\n';
}
int main ()
{
#ifndef ONLINE_JUDGE
freopen("1.in","r",stdin);
freopen("1.out","w",stdout);
#endif
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
int T;
cin>>T;
while(T--) solve();
return 0;
}
B
首先 \(n\) 為 \(1\) 到 \(5\) 時,直接輸出樣例。到 \(n>5\) 的時候,\(n\) 為奇數就是 \(36366\) 每次在前面加上 \(33\),否則就是 \(3366\) 每次在前面加上 \(33\)。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
#include <queue>
#include <map>
using namespace std;
typedef long long ll;
const int N=1;
int n;
void solve()
{
cin>>n;
if(n==1||n==3) cout<<-1<<'\n';
else if(n==2) cout<<66<<'\n';
else
{
if(n&1)
{
for(int i=1;i<=n-5;i+=2) cout<<33;
cout<<36366<<'\n';
}
else
{
for(int i=1;i<=n-4;i+=2) cout<<33;
cout<<3366<<'\n';
}
}
}
int main ()
{
#ifndef ONLINE_JUDGE
freopen("1.in","r",stdin);
freopen("1.out","w",stdout);
#endif
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
int T;
cin>>T;
while(T--) solve();
return 0;
}
C
構造題,觀察到 \(5 \le n\),不妨就考慮最後幾位,因為可以保證最後幾位受到的影響最小,思路是先考慮或出來最大,再考慮與上某個數不會影響或的數。
- \(n\) 為奇數,最後一次運算是按位與,所以 \(k \le n\),且 \(n\) 必須在最後一位,前面按位或的結果要保留 \(n\) 有的所有位,不妨就只保證等於 \(n\)。將 \(n\) 拆開,用最後一位 \(1\),也就是 \(lowbit(n)\) 和 \(n-lowbit(n)\) 相或得到 \(n\),然後要保證 \(lowbit(n)\) 不被影響,可以與上 \(lowbit(n)\) 加上一位小的 \(1\),這樣的話可以確定最後四位:
\[lowbit(n),lowbit(n)+lowbit(n)==1 ? 2 : 1,n-lowbit(n),n
\]
- \(n\) 為偶數,最後一次運算是按位或,所以可以填充所有位 \(k \le 2^t-1\),\(t\) 表示 \(n\) 的二進位制下的位數。
- 考慮特殊情況 \(n=2^{t-1}\),這樣的話最高位就只能是 \(n\) 來給,所以不妨讓最後一位為 \(n\),然後前面的結果就是要為 \(n-1\),但顯然直接或上 \(n-1\) 的話不可能保住它,所以將 \(n-1\) 再拆開成 \(1\) 和 \(n-2\),用 \(3\) 保住 \(1\),用 \(n-1\) 保住 \(n-2\),這樣的話就能確定最後五位:
\[1,3,n-2,n-1,n \]- 否則,用 \(n\) 的最高位 \(2^{t-1}\),和 \(2^{t-1}-1\) 拼湊成 \(2^t-1\)。所以確定最後三位:
\[2^{t-1},n,2^{t-1}-1 \]
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
#include <queue>
#include <map>
using namespace std;
typedef long long ll;
const int N=2e5+5;
int n;
int ans[N],v[N];
void solve()
{
cin>>n;
for(int i=1;i<=n;i++) ans[i]=0,v[i]=i;
int a,b,c,d=0,e=0;
if(n&1)
{
a=n&-n;
cout<<n<<'\n';
if(a==1) b=3;
else b=a+1;
c=n-a,d=n;
ans[n]=d,ans[n-1]=c,ans[n-2]=b,ans[n-3]=a;
}
else
{
int t=1;
while(t<=n) t<<=1;
cout<<t-1<<'\n';
if(n!=t/2)
{
a=t/2,b=n,c=t/2-1;
ans[n]=c,ans[n-1]=b,ans[n-2]=a;
}
else
{
a=1,b=3,c=n-2,d=n-1,e=n;
ans[n]=e,ans[n-1]=d,ans[n-2]=c,ans[n-3]=b,ans[n-4]=a;
}
}
v[a]=v[b]=v[c]=v[d]=v[e]=0;
int cnt=0;
for(int i=1;i<=n;i++)
{
if(ans[i]) continue;
while(!v[cnt]) cnt++;
ans[i]=v[cnt++];
}
for(int i=1;i<=n;i++) cout<<ans[i]<<' ';
cout<<'\n';
}
int main ()
{
#ifndef ONLINE_JUDGE
freopen("1.in","r",stdin);
freopen("1.out","w",stdout);
#endif
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
int T;
cin>>T;
while(T--) solve();
return 0;
}
D
結論比較好猜,就是儘可能將 \(2\) 都乘到最大的數上,但是有一個問題,前面的數不能乘後面的 \(2\),就是說原本後面的數更小,但是可以乘上更多的 \(2\)。
因此將 \(a_i\) 的 \(2\) 拆出來統計個數,用一個單調棧維護,棧內單調遞減,每次加入一個數,如果棧頂的元素小於這個數,就把棧頂的 \(2\) 全部給新加入的數。注意這裡的新數大小是要目前有的 \(2\) 的。注意乘上以後會爆 long long。細節看程式碼吧。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <vector>
#include <queue>
#include <map>
using namespace std;
typedef long long ll;
const int N=2e5+5,mod=1e9+7;
int n;
ll a[N],v[N],b[N];
int st[N];
int qpow(int x,int y)
{
int ret=1;
while(y)
{
if(y&1) ret=1ll*ret*x%mod;
x=1ll*x*x%mod;
y>>=1;
}
return ret;
}
ll count(ll &x)
{
if(!x) return 0;
int ret=0;
while(x%2==0) x/=2,ret++;
return ret;
}
ll restore(ll x,ll y)
{
while(y)
{
x<<=1;
if(x>mod) return mod;
y--;
}
return x;
}
void solve()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i],v[i]=count(a[i]);
int tot=0;
ll ans=0;
for(int i=1;i<=n;i++)
{
ans=(ans+a[i]*qpow(2,v[i])%mod)%mod;
while(tot&&a[b[tot]]<restore(a[i],v[i]))
{
ans=(ans-a[b[tot]]*qpow(2,v[b[tot]])%mod+mod)%mod;
ans=(ans+a[b[tot]])%mod;
ans=(ans-a[i]*qpow(2,v[i])%mod+a[i]*qpow(2,v[i]+v[b[tot]])%mod+mod)%mod;
v[i]+=v[b[tot]];
tot--;
}
b[++tot]=i;
cout<<ans<<' ';
}
cout<<'\n';
}
int main ()
{
#ifndef ONLINE_JUDGE
freopen("1.in","r",stdin);
freopen("1.out","w",stdout);
#endif
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
int T;
cin>>T;
while(T--) solve();
return 0;
}