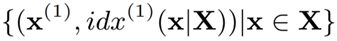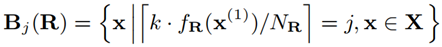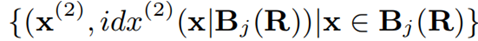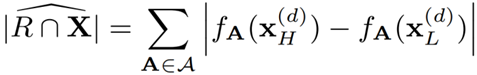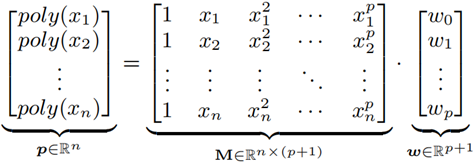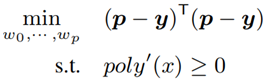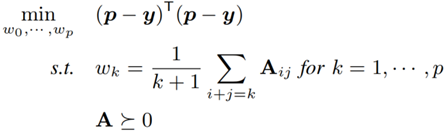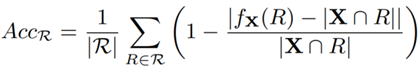編者按
本文系東北大學李俊虎所著,也是「 OceanBase 學術加油站」系列第九篇內容。
「李俊虎:東北大學電腦科學與工程學院在讀碩士生,課題方向為資料庫查詢最佳化,致力於應用 AI 技術改進傳統基數估計器,令資料庫選擇最優查詢計劃。」
今天分享的主題是 《HIST,面向海量資料的學習型多維直方圖》,從學習型索引方法的 RMI 模型借鑑了結構設計,並在此之上提出了學習型多維直方圖,即 LHIST (Learned Histogram) 模型,用於基數估計的學習型資料概要方法。希望閱讀完本文,你可以對這個話題有新的收穫,有不同看法也歡迎在底部留言探討。
*原文"LHist : Towards Learning Multi-dimensional Histogram for Massive Spatial Data",發表於 ICDE 2021,可點選文末“閱讀全文”下載全篇論文檢視。
多維直方圖 (Multi-dimensional histogram, MH) 技術被廣泛用於查詢的基數估計,空間資料分片,空間資料探勘等方向。然而,目前的 MH 方法存在以下缺陷:
- 不合理的假設: 為了減少空間代價,MH 和其它的資料摘要方法一樣需要隨機取樣過程,這極度依賴 dimension-wise independence 或者 intra-bucket uniform distribution 兩個理想化的假設。
- 不穩定的效能: 目前已有的 MH 方法的估計效果很容易受不同資料集的影響,引數設定,查詢負載等。已經有研究證明瞭 MH 的高準確率需要更高的儲存代價。
受最近提出的學習型索引模型的啟發,比如 RMI 模型 [1]透過整合簡單的機器學習模型改進廣泛使用的 B-tree 索引結構。本文從學習型索引方法的 RMI 模型借鑑了結構設計,並在此之上提出了能解決上述兩種缺陷的學習型多維直方圖,即 LHIST (Learned Histogram) 模型,它是一個完全由資料驅動的,可用於基數估計的學習型資料概要方法。LHIST 模型的設計有兩方面:
第一,可描述複雜多維直方圖的累計密度函式 CDF。
第二,能很好地平衡記憶體和準確率兩項指標。
實驗證明 LHIST 在儲存成本,查詢處理效率和精度方面都要優於傳統的資料概要方法。
問題定義
資料點 Point:一個向量 x = (x(1), x(2),..., x(d)) 是一個歐幾裡得空間,其中 x(i)表示向量 x 的第 i 維元素。
超矩形 Hyper-rectangle:一個超矩形可被符號化定義,如下
公式 1 超矩形定義
超矩形解析自查詢語句,每個陣列表示了謂詞的覆蓋區間,比如 age > 18 AND age < 24 可以被解析為 [18, 24]。使用 X 表示空間資料集,則 X ∩ R 表示某個查詢所覆蓋到的資料空間,| X ∩ R | 則表示該查詢的 COUNT 結果 (或者稱之基數)。
學習型空間概要 Learned Spatial Synopsis:定義一個函式 f ,它接受 R 作為輸入,並輸出 |X ∩ R|。
學習型索引RMI
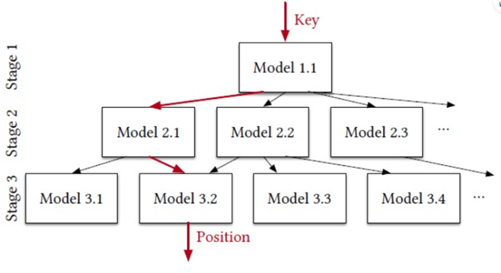
本文的模型結構借鑑於[1]提出的 RMI ( Recursive Model Index ),它是一個學習型索引模型,用於挖掘鍵值 key 以及排序索引位置 idx(key) 的關係。RMI 是一個層次結構 (而非樹形結構),當輸入 key 值時,模型會依據自身結構自上而下地進行搜尋,並在葉子節點返回預測的索引位置 idx(key)。
更具體來講,每一層 stage 的模型會預測 key 值的索引位置範圍,並據此決定繼續傳遞給下一層 stage 的哪個模型。越靠近底層的模型越能給出更加精確的預測,縮小搜尋範圍。顯然,RMI 模型本身由多個小型的模型組成,相比於單個的大型模型,這些小型模型的組合更易於訓練,節省空間和算力。
圖 1 RMI 模型的層次結構
簡而言之,RMI 的核心思想是將整個 key 空間分解成更小的空間,這樣索引位置分佈的累計密度函式 CDF 就更容易使用多個小型的線性模型去擬合。根據[1]的實驗表明,相比於 B-tree 結構,該架構的學習型索引能夠將儲存代價降低 99%。
RMI 可以用作一維資料概要,因為它本質上表示主鍵分佈函式 CDF,這類似於一維直方圖等其他統計概要結構。然而,要將這個想法擴充套件到多維資料具有挑戰性,因為與一維資料不同,多維資料點之間沒有明確的排序順序。
有一種解決方案是藉助空間填充曲線,將 k 維空間資料對映成 1 維,隨後使用降維的資料訓練 RMI 模型。諸如 z-order 曲線或者是 Hilbert 曲線都是可行的降維方案,但問題在於,在資料降維的過程中存在資訊丟失,因此基於這種方案的擴充 RMI 方法會損失部分估計的精確度。
另一種方案則是直接用模型學習空間資料的聯合分佈函式,最近提出的 Naru [2]和 DeepSPACE [3]就是典型的,透過自迴歸模型擬合多維資料聯合分佈的例子。這些研究均宣稱它們的模型顯著改善了基數估計的準確性,然而這些模型仍然不能很好地實現準確率與儲存空間的平衡。
本文則基於 RMI 的架構之上提出了對 MEH 的改進方案。
LUIST結構
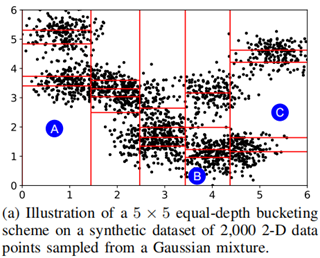
圖 2 MEH 對 2D 資料的切分演示
首先以二維 (d = 2) 多維等深直方圖 MEH 為例子,設 bucket = 5。首先在 "縱向" 按照等深策略分割空間資料 X,即 5 個資料域內的樣本點數量保持相同;其次,按照同樣的策略對每個資料域再進行 "橫向" 切割,並最終得到 5 × 5 = 25 個等深區域。
本文提出的 LHIST 模型可以被概括為學習型 MEH。即,相較於上述的等深 "硬分割" 策略,本文使用簡單的線性模型對每一維度的資料邊界進行 "軟分割",每個資料區域稱之為桶 bucket。
圖 3 LHSIT 結構展示
LHIST 則仿照 RMI 的層次結構構建了一個完全 k 叉樹迴歸模型,如圖 3 所示,其中 k 為每一個資料維度的劃分數量。設資料點 x 是一個 d 維向量,則迴歸模型將沿著自上而下的 stage 依次對這 d 維資料列進行分割。
LHIST 在前 d - 1 的 stage 將整個 d 維資料集分解成小桶,然後在最後一層 stage 訓練模型來近似桶內分佈 CDF。與之前簡單地將直方圖與擬合曲線相結合的研究不同 [4],本文 LHIST 模型的桶分割槽策略和桶內分佈 CDF 估計都是由簡單機器學習模型實現得到,它們很容易被最佳化。為此,LHIST 可以生成一個完全資料驅動的分桶方案,同時避免不切實際的假設,最終構建出一個高效,低儲存的多維直方圖。
LHIST 的結構能以遞迴的形式進行定義。在 LHIST 的第一個 stage 定義根節點 R,它代表了整個資料集。fR 表示了迴歸模型,它接受輸入向量 x,並首先輸出 x 在第 1 個維度的索引位置 idx(1)(x) ,即:
公式 2 根節點在第 1 維對資料劃分
在 LHIST 中,可以使用任何一個以非遞減作為約束條件的迴歸模型。在訓練 fR 之後,整個資料集 X 將被劃分成 k 個桶。從 R 節點劃分出的第 i 個桶可以符號化表示為:
公式 3 節點的資料分片記作 Buckets
每個桶 Bj(R) 將沿著第 2 個維度繼續搜尋索引位置 idx(2)(x),即:
公式 4 基於 Buckets 在第 2 維繼續對資料劃分
推廣到更一般的情形,對於第 i 個層級 ( i = 2,..., d - 1 ) 的任意一個節點 A,令 XA 表示 A 節點覆蓋的資料空間,記 NA = |XA|。
在構建 LHIST 之後,模型將在前 d - 1 個 stage 中把整個資料空間 X 分成 k d-1個桶,每個桶最終都將關聯一個葉子節點。最後第 d 層的葉子節點將負責構造第 d 維資料的桶內分佈。
對於給定分為查詢所對應的超矩形 R,其基數估計可以符號化表示為:
公式 5 將基數估計問題轉換為節點求和問題
其中,超矩形 R 所覆蓋的葉子節點 A 構成了一個集合。對於被覆蓋的每個節點 A,模型透過 x(d) 謂詞的範圍計算出當前節點的基數估計結果。比如,給定一個謂詞 [20, 40],基數 = |fA(40) - fA(20)|。而又由於每個葉子節點之間是相互獨立的,因此將所有被覆蓋節點的結果做加和即可求得某範圍查詢 R 對應的 COUNT 基數。
與 RMI 相比,LHIST 是一個嚴謹的樹形結構,而 RMI 結構中的一個子節點可以存在多個父節點,這會導致 RMI 模型需要更多的空間來儲存引數,維持層次結構。
函式選擇
前文曾提及 fA 可以是任意一個非遞減的迴歸模型。但實際上,模型的選擇對 LHIST 的精度和儲存運算產生深刻的影響。
作為最簡單的模型,線性迴歸模型 (比如 f(x) = ax + b) 非常容易儲存和訓練。然而,僅使用線性函式很難描述現實資料中複雜的 CDF。另一方面,雖然模型的層次越深,就越能描述複雜的 CDF,但是這會導致引數調優變得異常困難,這樣的模型不符合 LHIST 的效能要求。
作為效能和儲存的最佳權衡,本文選取了單變數多項式函式,它能夠靈活地控制模型的複雜度,即 ploy(x) = w0 + w1·x + ... + wp · xp,p 作為多項式的度數。使用者可以透過設定 p 來決定更高的精度,或者是更低的儲存空間。
假定 {(xi, yi)}i=1,...n 是一組容量為 n 的樣本點,其中 yi∈{ 1, ... , n } 是 xi 對應的索引次序,緊接著,一組 poly(xi) 的擬合函式可以如下表示:
公式 6 權值 W 即模型的最佳化目標
令 y = [y1, ... , yn]T 是參考值向量,p 是預測值向量。本文的建模問題可以轉換為最小二乘問題:
公式 7 將基數估計轉換為最小二乘問題
此處設定條件約束 ploy'(x)≥0 的目的是保證 ploy(x) 是非遞減函式,這滿足 CDF 的語義。進一步,本文透過數學方法將非遞減作為約束的最小二乘問題轉化成了半正定規劃:
公式 8 將公式 7 轉換為半正定規劃問題
最終,模型透過該規劃的約束條件學習 W = [w0, w1, ... wp] T,並使得模型的誤差最小。
與MEH方法的比較
和單純的 MEH 方法相比,LHIST 對儲存預算的利用率更高。本質上,每一條 MEH entry 都需要一個整數儲存頻率,並且使用一個浮點數儲存桶的邊界。給定同等的儲存空間,經過訓練的緊湊型迴歸模型可以在不作任何理想假設的前提下編碼更多的區域性分佈資訊。
在相同的儲存預算下,本文的 LHIST 在精度方面比 MEH 高出 24 倍,執行效率方面則比 MEH 高出 1.8 倍。
▋實驗部分
一、資料集及其引數設定
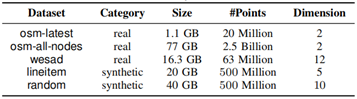
本實驗中使用的資料集如下:
表 1 實驗用空間資料集
作為對比實驗,本實驗對以下超引數進行了不同的設定:
表 2 對記憶體,多項式度,選擇率的設定
參與比較的方法有:
表 3 參與對比的多種模型
隨機取樣法。隨機取樣法有兩種策略,即簡單隨機取樣 (RS) 以及分層取樣 (SS)。
多維直方圖。和 [5]類似,本文實現了兩種直方圖作為對比,即均勻直方圖 (UH) 以及多維等深直方圖 (MEH)。
RMI。如前文所述,當前的方法結合了 z-order 方法實現了 1-D RMI 線性迴歸模型,以構建資料概要。
深度無監督學習。這裡使用了具有代表性的 Naru 模型,本文按照由小到大的次序建立了三個不同規模的模型例項:Naru-s (small),Naru-m (middle),Naru-l (large)。
LHIST。本文實現了三種 LHIST 結構:LHIST + 線性迴歸 (l-LHIST),LHIST + 分段線性迴歸 (plr-LHIST),LHIST + 多項式迴歸 (p-LHIST)。
為了評估基數估計器的準確度,這裡選取公式 9 作為評估標準:
公式 9 模型衡量指標
二、準確度評估
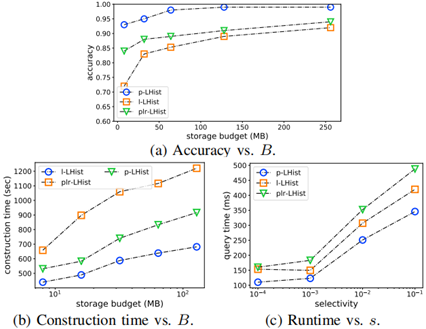
圖 4 不同模型在不同選擇率下的準確率效能
圖 4 繪製了範圍查詢的基數估計模型在不同記憶體預算下的準確率表現。通常情況下,給定更多的預算 B 能夠提高以上方法的準確率。除了 RMI 方法之外,其它方法在預算足夠 (budget = 128 MB) 且查詢選擇度足夠高的情形下 (Selectivity = 10 -1) 能夠達到超過 95% 的準確率,這驗證了前文的觀點:應用 z-order 等降維手段會影響 RMI 模型估計的準確率。
與 Naru 相比,LHIST 能夠在選擇度 >10 -3的情況下達到相近的效能。然而 LHIST 在低選擇度查詢的表現則更加穩定。在低選擇度下,增加 Naru 的神經元數量反而會降低準確率,因為 DL 模型學習聯合分佈的過程是不可解釋的;而 LHIST 則可以用很小的記憶體預算保留多維資料的完整資訊。
三、構建代價
傳統資料概要方法的構建代價顯然要更小,因此這裡重點觀察並對比學習型的方法:Naru,RMI,以及 LHIST。結果對比見圖 5:
圖 5 不同模型基於不同資料集的構建代價
在學習型資料概要方法中,LHIST 的構建時間總體最短,僅比非學習型的 MEH 方法稍微耗時一些。值得注意的是,Naru 總是需要最多的模型構建時間。尤其是在最大的資料集 osm-all-nodes 上,Naru-m 需要將近 8 小時的時間進行訓練,這主要是受到了 GPU 記憶體限制的影響。
四、推理時延
圖 6 不同模型在不同記憶體預算下的推理時延
圖 6 展示了 osm-all-nodes 資料集上,不同模型對範圍 COUNT 查詢的處理時延。本文使用了字首和技巧最佳化了均勻直方圖 UH,因此在當前的實驗中,它只需要常數量級的代價。
RMI 的處理效率接近於常量,因為它只需要計算R 的下邊界 R.xH 和上邊界 R.xL;Naru 的處理效率接近於常量,這主要取決於模型的複雜度。
本文透過實驗觀察到,LIHIST 模型要比 MEH 的效率高出 1.1 ~ 1.9 倍。這是因為 MEH 的桶分割槽是非均勻的,因此該方法需要多輪二分查詢才可以定位到某個區域,尤其是分桶變得十分複雜時,MEH 的查詢將消耗顯著的時間。相比之下,LHIST 只需要經過固定的 d 層 stage,且每一層模型都是簡單的多項式。
五、不同子模型的選擇
本文比較了 LHIST 下的幾個不同子模型,並且在 wesad 資料集上做了實驗,實驗結果如圖 7。
圖 7 不同函式選擇對推理效率的影響
總體來說,使用多項式作為 fA 能夠在效率和準確率當中達到一個最佳的平衡。與 l-LHIST 方法相比,p-LHIST 只需要更少的桶數量,因此它可以更快地遍歷 HLIST 樹。不僅如此,p-LHIST 可以在非常有限的記憶體預算中達到更高的準確率。
六、多項式度 p 的影響
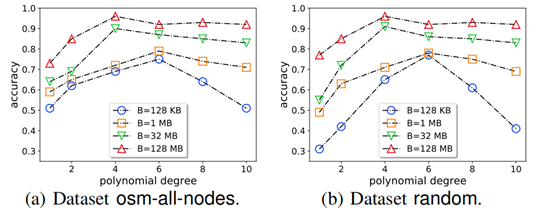
為了測試不同 p 對 p-LHIST 效能的影響,本文分別在 osm-all-nodes 和 random 兩個資料集下做了兩個實驗,這裡將測試查詢的選擇度固定為 10 -3。
圖 8 p 值對準確率的影響呈單峰函式
可以觀察到影像接近單峰函式,當 p ∈ [4, 6] 時,模型的準確率接近達到最高值。除此之外,研究還表明,當模型需要處理高維資料時,選取最佳的度數 p 將變得至關重要。這是因為維度 d 越大,則資料空間越稀疏。此時需要更加細粒度的資料劃分,從而保證桶內的資料分佈 CDF 更加容易學習。
相關工作
本文首先討論並比較已有的資料概要以及學習型索引。
- 直方圖。 多維直方圖可以聯合資料分佈的近似。STHoles [6]是一種查詢驅動的直方圖方法,根據查詢負載來對資料進行分割槽。本文的方法則是完全資料驅動的方法,並將未來的負載感知最佳化作為未來的工作。
- 學習型索引。 已有的研究已證明瞭 B-tree 的索引結構可以被簡單的機器學習模型所替代,比如 RMI [1]。目前還有很多學者開始了對學習型索引的研究。比如 Ding 等人提出了名為 ALEX [7]的,可適應動態負載的學習型 B-tree。
如本文所述,想要將 1-D 學習型索引擴充到多維資料庫是一個具有挑戰的任務,因為資料點通常沒有明確的排序關係。
- AI in DB。 除了學習型索引之外,機器學習還廣泛地應用到了連線代價估計, [8], [9],查詢最佳化器 [10], [11],和 DBMS 自調參 [12], [13]。
本文的工作可被歸類為學習型基數估計以及近似查詢處理,如 DeepSPACE 和 Naru 模型。然而,目前的學習型估計器的通用性較差,主要是無法實現儲存和精度之間的權衡。
寫在最後
本文提出的 LHIST 屬於空間資料概要框架,它可被看作是 MEH 的學習型版本。LHIST 完全由資料驅動,並且不依賴專家經驗調整模型引數。經過實驗表明,LHIST 在效率和準確率方面均優於傳統的資料摘要方法。
*參考文獻:
[1] T. Kraska, A. Beutel, E. H. Chi, J. Dean, and N. Polyzotis, “The case for learned index structures,” in SIGMOD Conference. ACM, 2018, pp. 489–504.
[2] Z. Yang, E. Liang, A. Kamsetty, C. Wu, Y. Duan, P. Chen, P. Abbeel, J. M. Hellerstein, S. Krishnan, and I. Stoica, “Deep unsupervised cardinality estimation,” PVLDB, vol. 13, no. 3, pp. 279–292, 2019.
[3] D. Vorona, A. Kipf, T. Neumann, and A. Kemper, “DeepSPACE: Approximate geospatial query processing with deep learning,” in SIGSPATIAL/GIS. ACM, 2019, pp. 500–503.
[4] A. C. König and G. Weikum, “Combining histograms and parametric curve fitting for feedback-driven query result-size estimation,” in VLDB. Morgan Kaufmann, 1999, pp. 423–434.
[5] A. B. Siddique, A. Eldawy, and V. Hristidis, “Comparing synopsis techniques for approximate spatial data analysis,” Proc. VLDB Endow., vol. 12, no. 11, pp. 1583–1596, 2019.
[6] N. Bruno, S. Chaudhuri, and L. Gravano, “STHoles: A multidimensional workload-aware histogram,” in SIGMOD Conference. ACM, 2001, pp. 211–222.
[7] J. Ding, U. F. Minhas, J. Yu, C. Wang, J. Do, Y. Li, H. Zhang, B. Chandramouli, J. Gehrke, D. Kossmann, D. B. Lomet, and T. Kraska, “ALEX: an updatable adaptive learned index,” in SIGMOD Conference. ACM, 2020, pp. 969–984.
[8] J. Sun and G. Li, “An end-to-end learning-based cost estimator,” PVLDB, vol. 13, no. 3, pp. 307–319, 2019.
[9] B. Hilprecht, A. Schmidt, M. Kulessa, A. Molina, K. Kersting, and C. Binnig, “DeepDB: Learn from data, not from queries!” Proc. VLDB Endow., vol. 13, no. 7, pp. 992–1005, 2020.
[10] R. C. Marcus, P. Negi, H. Mao, C. Zhang, M. Alizadeh, T. Kraska, O. Papaemmanouil, and N. Tatbul, “Neo: A learned query optimizer,” PVLDB, vol. 12, no. 11, pp. 1705–1718, 2019.
[11] C. Wu, A. Jindal, S. Amizadeh, H. Patel, W. Le, S. Qiao, and S. Rao, “Towards a learning optimizer for shared clouds,” PVLDB, vol. 12, no. 3, pp. 210–222, 2018.
[12] T. Kraska, M. Alizadeh, A. Beutel, E. H. Chi, A. Kristo, G. Leclerc, S. Madden, H. Mao, and V. Nathan, “SageDB: A learned database system,” in CIDR. www.cidrdb.org, 2019.
[13] S. Idreos, N. Dayan, W. Qin, M. Akmanalp, S. Hilgard, A. Ross, J. Lennon, V. Jain, H. Gupta, D. Li, and Z. Zhu, “Design continuums and the path toward self-designing key-value stores that know and learn,” in CIDR. www.cidrdb.org, 2019.