Nebula Graph 原始碼解讀系列 ｜ Vol.06 MATCH 中變長 Pattern 的實現


## 目錄

- 問題分析

    - 定長 Pattern

    - 變長 Pattern 與變長 Pattern 的組合

- 執行計劃

    - 擴充一步

    - 擴充多步

    - 儲存路徑

    - 變長拼接

- 總結

MATCH 作為 openCypher 語言的核心，透過簡潔的 Pattern 形式，可以讓使用者方便地表達相簿中的關聯關係。變長模式又是 Pattern 中用來描述路徑的一種常用形式，對變長模式的支援是 Nebula 相容 openCypher MATCH 功能的第一步。

由之前的系列文章可以瞭解到，Nebula 的執行計劃是由許多的物理運算元組成，每個運算元都負責執行特有的計算邏輯，在 MATCH 的實現中也會涉及前述文章中的這些運算元，比如 GetNeighbors、GetVertices、Join、Project、Filter、Loop 等等。因為 Nebula 的執行計劃不同於關聯式資料庫中的樹狀結構，在執行的流程上其實是一個有環的圖。如何把 MATCH 中的變長 Pattern 變成 Nebula 的物理計劃是 Planner 要解決的問題的重點。以下便簡單介紹一下在 Nebula 中解決變長 Pattern 問題的思路。

## 問題分析

### 定長 Pattern

在使用 MATCH 語句時，定長 Pattern 也是比較常用的查詢形式。如果把定長 Pattern 理解成向外擴充 X 步的變長 Pattern，認為其是後者的一種特例，那麼定長和變長 Pattern 的實現便可以統一起來，如下所示：

```shell

// 定長 Pattern MATCH (v)-[e]-(v2)

// 變長 Pattern MATCH (v)-[e*1..1]-(v2)

```

上述示例中的區別就是變數 e 的型別，定長時 e 表示的是一條邊，而變長時 e 表示的是長度為 1 的邊列表。

### 變長 Pattern 與變長 Pattern 的組合

在 openCypher 的 MATCH 語法裡，Pattern 可以靈活的組合以表達複雜路徑。如下所示，變長 Pattern 再接變長 Pattern：

```shell

MATCH (v)-[e*1..3]-(v2)-[ee*2..4]-(v3)

```

上述的過程可以是個不斷延伸的過程，透過變長定長模式的不同排列，可以組合出非常複雜的路徑。所以我們必須找到一種生成 plan 的模式才能方便的遞迴迭代整個過程。其中需要考慮如下的因素：

1. 後面變長 Pattern 的路徑依賴前面所有變長路徑；

2. 變長 Pattern 後面的所有的符號（或者變數）表示的結果是“變化”的；

3. 每一步在往外擴充之前需要對起點進行去重；

我們可以注意到，如果可以生成 Pattern 中 `()-[:like*m..n]-` 的部分的執行計劃，那麼後面繼續進行組合迭代就變得有跡可循，如下所示：

```shell

()-[:like*m..n]- ()-[:like*k..l]- ()

 \____________/   \____________/   \_/

    Pattern1         Pattern2       Pattern3

```

## 執行計劃

下面便分析模式中 `()-[:like*m..n]-` 的部分，檢視其如何轉換成 Nebula 的物理執行計劃的。上面模式描述的意思是向外擴充 m 到 n 步，在 Nebula 中向外擴充一步是透過 GetNeighbors 運算元完成的。如果要向外擴充多步，需要不斷在上一步擴充的基礎上再呼叫 GetNeighbors 運算元，將每次獲取的點邊資料首尾連線就會拼接成一個路徑（path）。雖然使用者最後需要的只是 m 到 n 步的路徑，但是在執行的過程中依然需要從第 1 步開始擴充直到第 n 步。並且每步擴充過程中的路徑結果都需要儲存下來，以便輸出或者給下一步使用。最後只要拿出長度在區間 m 到 n 步之間的路徑即可。

### 擴充一步

先來看看走一步的計劃是什麼樣子，因為 Nebula 資料儲存的方式為起點和出邊放置在一起，所以獲取起點和出邊的資料是不需要跨 partition 的。但是邊的終點資料一般是跨 partition 的，需要單獨透過 GetVertices 介面來獲取點的屬性。除此之外，在向外擴充之前，最好要把擴充的起點資料進行去重，避免 storage 重複掃描。所以走一步的執行計劃如下圖所示：


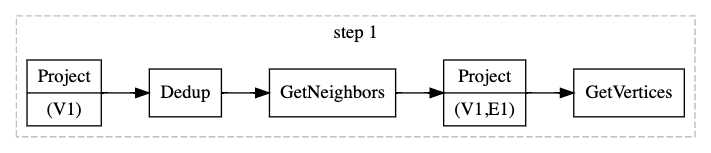
### 擴充多步

擴充多步的過程其實就是將上述的過程重複，但是我們會注意到 GetNeighbors 可以獲取起點的屬性，所以在擴充下一步時，是可以省掉一步 GetVertices 操作。擴充兩步的執行計劃就變為：


### 儲存路徑

由於最後可能需要返回每一步擴充的路徑，所以在上述擴充過程中，還需要將所有的路徑進行儲存。連線兩步之間的路徑可以透過 join 運算元完成。同時因為模式 `()-[e:like*m..n]-` 的返回結果中 e 表示的是一列資料（邊的 list），所以上面每步擴充路徑需要透過 union 的方式進行結果集的合併。執行計劃進一步演變為：


### 變長拼接

由上面的過程便可以生成模式  `()-[e:like*m..n]-` 的物理計劃，當多個類似模式做拼接時，就是再把上述的過程進行迭代。不過在進行模式迭代之前，還需要對上面計劃得到的結果進行過濾，因為我們期望是得到 m 到 n 步的結果，上面的資料集中包含了從第 1 步到第 n 步的所有結果，透過對路徑的長度做個簡單的篩選即可。變長模式拼接之後的計劃變為：


透過上述一步步的分解，我們終於得到了最初 MATCH 語句期望的執行計劃，可以看到在把一個複雜模式轉換成底層的擴充介面時還是頗費功夫。當然上面的計劃可以做些最佳化，比如把多步擴充的過程使用 Loop 運算元進行封裝，複用一步擴充的 sub-plan，這裡不再詳細展開。感興趣的使用者可以參考 [nebula 原始碼實現]()。

## 總結

上述過程演示了一個變長 Pattern 的 MATCH 語句的執行計劃生成過程，相信大家這時會有這樣一個疑惑，為什麼基本的一些路徑擴充在 Nebula 中會生成這麼複雜的執行計劃？對比 Neo4j 的實現，幾個運算元即可完成相同的工作，在這裡會變成繁瑣的 DAG 呢？

這個問題的本質原因是 Nebula 的運算元更接近底層的介面，缺少一些更上層的圖操作語義上的抽象。運算元力度太細，就會導致上層的最佳化等實現需要考慮太多的細節。後面會對執行運算元進一步的梳理，來逐步的完善 MATCH 功能和提升效能。

《開源分散式圖資料庫Nebula Graph完全指南》，又名：Nebula 小書，裡面詳細記錄了圖資料庫以及圖資料庫 Nebula Graph 的知識點以及具體的用法，閱讀傳送門：[]()

交流圖資料庫技術？加入 Nebula 交流群請先[填寫下你的 Nebula 名片](https://wj.qq.com/s2/8321168/8e2f/)，Nebula 小助手會拉你進群~~