關係模型資料庫系統的資料結構簡單，表示資料及其資料之間的聯絡均採用關係（二維表），同時關係模型有紮實的數學理論做基礎，使得資料的操作可以通過關係的運算來完成。

關係及關係模型

關係是數學上的一個概念，建立在日常生活中所論及的關係概念之上，例如我們通常所說的鄰里關係、朋友關係、學生與所選修的課程及該課程的成績關係等。在這裡我們所論及的朋友關係涉及到了互為朋友的雙方，在數學上可表示為(張,李)；鄰里關係也涉及到了互為鄰里的雙方，表示為(李家,張家)；學生與所選修的課程及該課程的成績關係，涉及到學生、所選的課程以及所取得的成績，在數學上表示為(李蘭,軟體基礎,90)。(李,張)、(李家,張家)、(李蘭,軟體基礎,90)在數學上稱為元組，括號裡用逗號隔開的物件，數學上稱為元組的分量。

數學上關係的概念是日常生活中關係概念的抽象，下面給出關係的簡單、直觀的概念：

1.關係

關係是以元組為元素的集合。資料庫技術中論及的關係概念應該是：關係是同型別元組的結合。

簡單說，關係就是集合，可以用大寫字母R1，R2，R來表示。

範例：學生與所選課程之間的關係R可以表示為：

R={(李蘭,軟體基礎,90),(張娜,高等數學,87),(張偉,C語言,76),…，(韶華,英語,79)}

這樣的一個關係R，在日常生活中可通常表示成一個表格的形式：

姓名	課程名	成績
李蘭	軟體基礎	90
張娜	高等數學	87
張偉	C語言	76
…	…	…
韶華	英語	79

我們可以看到，這張表表示一個關係，表中的每一行表示一個元組，也就是關係集合的元素，表格中每列的資料表示元組的分量。

2.關係模型

從上面的例子中可以看到，數學上關係的概念可以用來描述一個二維表，而二維表就是我們現實世界中進行各種檔案管理使用的方法，其中記錄了大量的資料。這樣就用數學理論中的一個概念描述了現實世界的一個物件。關係型資料庫就是用關係描述資料的資料庫系統。

（1）二維表與關係

　　關係可以用來描述二維表，對應的術語是：

• 關係←→二維表；
• 元組←→二維表中的行
• 分量←→二維表中的列

（2）二維表與關係型資料庫中的資料

一個關係型資料庫中的資料對應於一個二維表，其中對應的術語是：

• 二維表←→一個資料庫中的表、一個資料檢視
• 二維表的行←→資料表中的記錄
• 二維表的列←→表記錄的欄位

範例：

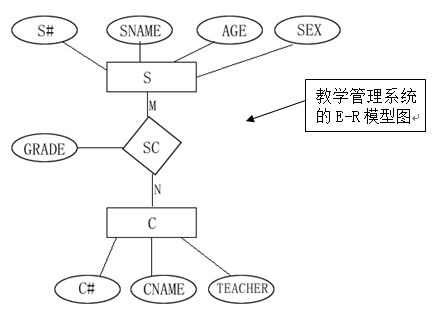
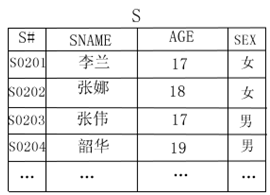
這裡的教學管理系統的E-R模型圖，其中實體“學生”的屬性為學號，姓名、年齡、性別，分別用S#,SNAME，AGE，SEX表示，實體“課程”的屬性為課程號，課程名，授課教師，分別用C#，CNAME，TEACHER表示，實體學生用S表示，課程用C表示，學生與課程之間的關係用SC表示，SC的屬性成績用GRADE表示。

用關係描述教學管理模型的資料：

分析：在這個E-R圖中，實體有學生和課程兩個，兩個實體之間的聯絡是多對多的，按照將E-R模型轉換成關係模型的轉換方法，由於學生實體與課程實體之間的聯絡是多對多的，所以轉換成關係模型時，實體和聯絡分別轉換為關係模式：

S(S#,SNAME,AGE,SEX)

C(C#,CNAME,TEACHER)

SC(S#,C#,GRADE)

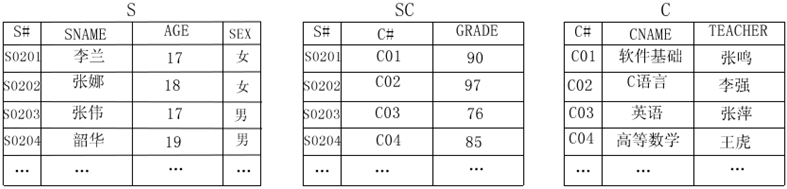
這些關係模式集可以描述三類關係，下面是這三類關係模式的關係例項：

上面的三個關係中，關係S的關鍵字是：S#(學號),關係C的關鍵字是：C#(課程號)，關係SC的關鍵字是：S#+C#(學號+課程號)。關鍵字是能唯一標識記錄的欄位或欄位表示式。這樣我們就將現實世界（教學管理系統）用S、C、SC三個關係模式描述清楚了。

（3）關係模型的三類完整性規則

關係描述了現實世界中的資料，這些資料以資料庫（表）的形式儲存到計算機中，根據現實世界的變化，計算機中的資料也要進行相應的改變。為了維護資料庫資料與現實世界資料的一致性，關聯式資料庫中的資料的建立與資料的更新必須遵守以下規則：

1. 實體完整性規則：實體完整性規則要求關係中，記錄關鍵字的欄位不能為空，不同記錄的關鍵字，欄位值也不能相同，否則，關鍵字就失去了唯一標識記錄的作用。
2. 參照完整性規則：參照完整性規則要求關係中“不引用不存在的實體。”

例如在聯絡關係SC中課程號欄位出現的課程號，必須在課程關係中存在，假如在關係C中找不到“小學算術”這個課程的課程號，而SC中出現了記錄：（李冰,CC01(小學算術)，95），那麼這條記錄就是一條錯誤的記錄，因為它違背了參照完整性規則

參照完整性規則可以理解如下：

如果屬性集K是關係模式R1的關鍵字，K也是關係模式R2的屬性，那麼在關係R2中K為外來鍵，在R2的關係中K的取值只允許有兩種可能，或者為空值，或者等於R1關係中某個關鍵字的值。

其中提到的外來鍵是指：當關系中的某個屬性或屬性組雖然不是該關係的關鍵字或只是該關係關鍵字的一部分，但卻是另一個關係的關鍵字，則成該屬性是這個關係的外來鍵，如上面提到的SC關係中的課程號不是SC的關鍵字，但課程號是關係C的關鍵字，因此課程號是SC的外來鍵，在關係SC中屬性課程名的值只能為空或者為C中課程號欄位中的某個值。

主鍵不能為空，並且不可以重複，外來鍵可以為空

　　3. 使用者完整性規則：這是針對某一具體資料的約束條件，由應用環境決定。使用者定義的完整性規則反映某一具體應用涉及的資料必須滿足語義的要求。系統提供定義和檢驗這類完整性的機制，以便用統一的方法處理它們，不再由應用程式承擔這項工作，例如在定義關係模式時，定義關係中的每個欄位，對每個欄位必須定義該欄位的欄位名（年齡），欄位型別（整型），欄位寬度（2位），小數位數（0位），經過這樣的定義，在給每條記錄的年齡欄位輸入資料時，可以輸入兩位整型資料，這就是一種約束，如果我們還想進一步對錄入的資料進行約束，以減少資料錄入的錯誤，需要定義一個具體的約束條件（可以寫一條規則），把年齡限制在15歲到25歲之間（實際上這是學生的實際年齡範圍），以滿足實際資料的需要，這就是使用者完整性規則，在進行資料操作時由系統負責檢驗資料的合理性。

總結前面關於關係模型的論述，我們看到，在定義一個關係模式時，需要進行以下三個部分的定義：

　　1) 資料結構的定義：資料庫中的全部資料及其互相聯絡都被組織成“關係”的形式，並且關係模型的基本資料結構也是關係。

　　2) 資料操作的定義：關係模型提供一組完備的高階關係運算，以支援資料庫的各種操作。關係運算分為關係代數和關係演算兩類。

　　3) 關係模型的三類完整性規則的定義：除了進行資料結構、資料操作的定義，為了確保資料的正確性，還要進行三類完整性規則的定義。

關係代數

　　關係是一個數學上的概念，是一類集合（以同型別元組為元素的結合），因此關係代數是以集合代數為基礎發展起來的，關係是可以進行運算的。如同數字運算的物件和結構都是數字、集合運算的物件和結果都是集合一樣，關係運算的物件和結果都是關係。關係運算可以分為兩類：

傳統的集合運算：這類運算從關係是集合的定義出發，把關係看出集合，則集合的所有運算對關係也是有效的。這類運算有：關係的並集、交集、差集、笛卡爾積。

專門的關係運算：這類運算是用來進行資料庫的查詢操作。這些運算可以把二維表進行任意的分割和組裝，隨機地由已有的二維表構造出各式各樣使用者所需要的二維表。這類運算有：投影、選擇、連線、除法運算。

1. 傳統的集合運算

　　傳統的集合運算是二元運算。所謂二元運算是指運算的物件為兩個，比如加法就是二元運算，進行運算的物件是兩個數；二元關係運算是指，兩個關係進行運算，結果為一個新關係。

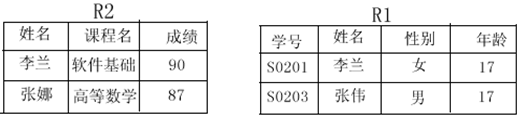
（1）關係的並運算

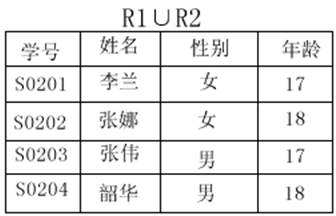
關係的並運算的運算子號與集合並運算的符號相同，都是∪，關係運算中，只有兩個同型別關係的並才有意義。設R1和R2是兩個同型別的關係，它們之間的並運算表示式是：R1∪R2，其結果也是同型別的關係，其中R1∪R2的元組或者是R1的元組或者是R2的元組，記為：

R1∪R2={t|t∈R1∨t∈R2}

“∨”這個符號的意思是“或”，即t是屬於(∈)R1裡面的元組，或者t是屬於R2裡面的元組。所以這裡的表示式的意思是R1∪R2產生了一個新的關係，這個新的關係由元組t組成，t可能是來自R1裡面的元組，也可能是來自R2裡面的元組。

範例：

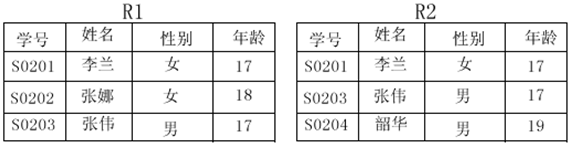
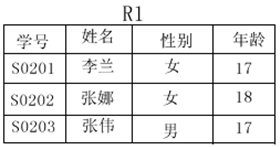
設R1、R2為學生實體模式下的兩個關係：

則由關係並的定義得R1∪R2

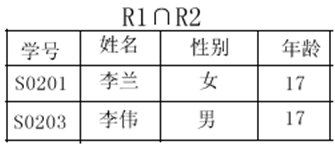
（2）關係交運算

　　關係交運算子號與集合交運算的符號相同，都是∩，關係運算中，只有兩個同型別關係的交才有意義。設R1和R2是兩個同型別的關係，它們之間的交運算表示式是：R1∩R2，其結果也是同型別的關係，其中R1∩R2的元組是由既是R1的元組也是R2的元組構成，記為：

R1∩R2={t|t∈R1∧t∈R2}

“∧”這個符號的意思是“且”，即t既是屬於(∈)R1裡面的元組，同時t也是屬於R2裡面的元組。所以這裡的表示式的意思是R1∩R2產生了一個新的關係，這個新的關係由元組t組成，t既是來自R1裡面的元組，也是來自R2裡面的元組。

範例：設R1、R2為上述範例中的學生實體模式下的兩個關係，求R1∩R2

由關係交運算的定義可得R1∩R2

（3）關係差運算

關係差運算的運算子合與集合差運算的符號相同，都是－，關係運算中，只有兩個同型別關係的差才有意義。設R1和R2是兩個同型別的關係，它們之間的差運算表示式是R1－R2，其結果也是同型別的關係，其中 R1－R2的元組是由R1的元組，而不是R2的元組構成，記為：

R1－R2={t|t∈R1∧t∉R2}

範例：設R1、R2為上述範例中的學生實體模式下的兩個關係，求R1－R2

由關係差運算的定義可得R1－R2

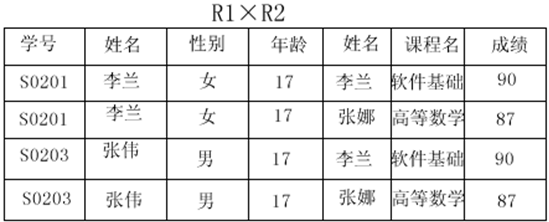
（4）笛卡爾積運算

笛卡爾積是關係這類集合所特有的一種運算，其運算子合是乘法運算子“×”，是一個二元關係運算，兩個運算物件可以是同型別的關係也可以是不同型別的關係，若R1是r1元元組的集合，R2是r2元元組的集合，則R1×R2是r1+r2元組的集合，R1×R2的元組(元組對應著二維表中的行)是由R1的分量(分量對應著二維表中的列)和R2的分量組成的，記為：

R1×R2={t|t=(r1,r2)∧r1∈R1∧r2∈R2}

範例：設關係R1、R2分別為學生實體和學生與課程聯絡的兩個關係，求R1×R2。

由笛卡爾積的定義可得R1×R2

從上例中我們看到R1×R2是一個很大的運算，由R1、R2進行笛卡爾積運算得到的新關係是比關係R1、R2大得多的關係。這個運算的運算量大、佔有的儲存空間大，並且我們看到在R1×R2關係中，四條記錄只有第一條記錄有實際意義的，而其他的三條記錄均沒有實際的意義。我們分析第一條記錄，又是一條非常有用的資訊，反映了李蘭同學的所有資訊包括她的學號、姓名、性別、年齡、選學的課程名以及所選課程的成績，這條記錄的資訊來源於兩個關係中，是兩個關係的一種連線。

2. 專門的關係運算

專門的關係運算有選擇、投影、關係的自然連線和關係的除法，其中關係的選擇運算和投影運算是一元運算，是對一個關係進行垂直和水平分解而得到一個關係，而關係的自然連線和關係的除法是二元運算，是把兩個關係的資訊根據需要組織成一個新關係，是資訊的綜合，這幾種關係的運算都與記錄的查詢操作有關。

（1）選擇運算

　　關係的選擇運算的運算子是“δ”，關係的選擇運算是一元運算，運算的物件是關係，運算的結果也是關係，新關係是原關係的子集，記為：

δF(R)={t|t∈R∧F(t)}

在上式中δ表示的是選擇運算，F是一個條件表示式，R是進行關係運算的物件，δF(R)是選擇運算的結果，其元組首先是關係R的元組，並且這些元組要使得條件F為真，即F(t)為真，因此，選擇運算也可敘述為：在關係R中選擇滿足條件F的記錄，組成一個新的關係

範例：設關係R1是實體學生關係模式的一個關係，在關係R1中查詢滿足年齡小於等於17的學生。

解決這個問題可以使用選擇運算來完成。

R=δ年齡≤17(R1)={t|t∈R1∧age≤17}

運算的結果為：

通過這個例子可以看到，關係的選擇運算可以用來在一個關係中查詢滿足條件的記錄，由這些滿足條件的記錄組成的新關係就是選擇運算的結果。在這個例子中條件是學生關係中記錄的年齡欄位的值小於等於17。選擇運算是對關係進行水平分割生成使用者需要的關係。

（2）投影運算

關係投影運算的運算子是“Ⅱ”，關係投影運算是一元運算，運算的物件是關係，運算的結果也是關係，新關係的元組是在原關係的元組中選出的若干個分量組成的元組，記為：

Ⅱti1,ti2,…tim(R)={t|t=(ti1,ti2,…tim)∧(t1,t2,…,tk)∈R}(其中K>im)

上式中“Ⅱ”是投影運算的運算子，R是投影運算的運算物件，(t1,t2,…，tk)是關係R的元組，(ti1,ti2,…tim)是投影運算所得到新關係的元組。

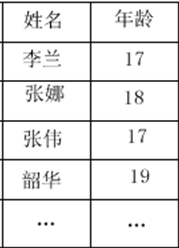
範例：設S是學生關係模式的一個關係，在某次查詢中要求查詢每個學生的年齡

解決這個問題，可以使用投影操作：

R=Ⅱ姓名,年齡(S)={t|t=(姓名,年齡)∧(學號，姓名，性別，年齡)∈S}

運算結果R為：

在關係R中查詢某個學生的年齡比在關係S中查詢某個學生的年齡運算量要小得多。

投影運算是對關係進行垂直分割，產生使用者所需要的關係

（3）連線運算

連線運算與投影和選擇運算不同，連線運算是將兩個關係連線起來，以滿足查詢任務的要求，連線運算是二元運算。實際上，關係笛卡爾積運算就是一種連線運算，是兩個關係的最大連線。笛卡爾積運算的結果，產生了很多沒有實際意義的記錄，而連線運算是將兩個關係連線起來，獲得與使用者查詢有關的新關係。關係的連線有兩類；條件連線和自然連線

轉載自：關係型資料庫理論