前言
zr遊記系列因作者在考試的重重打擊下,它,寄了。
作者還是寫下了這一片“網路流學習筆記”來紀念學會了網路流。
廢話不多說了,筆記要不是抄別人部落格的,要麼是抄老師課件的。
基本概念
關於網路流的
-
網路流 \((Net Work Flow)\): 一種類比水流的解決問題的方法。(下述概念均會用水流進行解釋)
-
網路 \((NetWork)\) : 可以理解為擁有源點和匯點的有向圖。(運輸水流的水管路線路)
-
弧 \((arc)\): 可以理解為有向邊。下文均用 “邊” 表示。(水管)
-
弧的流量 \((Flow)\) : 簡稱流量。在一個流量網路中每條邊都會有一個流量,表示為 \(f(x,y)\) ,根據流函式 \(f\) 的定義,\(f(x,y)\) 可為負。(運輸的水流量)
-
弧的容量 \((Capacity)\): 簡稱容量。在一個容量網路中每條邊都會有一個容量,表示為 \(c(x,y)\)。(水管規格。即可承受的最大水流量)
-
源點 \((Sources)\) : 可以理解為起點。它會源源不斷地放出流量,表示為 \(S\)。(可無限出水的 \(NB\) 水廠)
-
匯點 \((Sinks)\): 可以理解為終點。它會無限地接受流量,表示為 \(T\)。(可無限收集水的 \(NB\) 小區)
-
容量網路: 擁有源點和匯點且每條邊都給出了容量的網路。(安排好了水廠,小區和水管規格的路線圖)
-
流量網路: 擁有源點和匯點且每條邊都給出了流量的網路。(分配好了各個水管水流量的路線圖)
-
弧的殘留容量: 簡稱殘留容量。在一個殘量網路中每條邊都會有一個殘留容量 。對於每條邊,殘留容量$ =$容量 \(−\)流量。初始的殘量網路即為容量網路。(表示水管分配了水流量後還能繼續承受的水流量)
-
殘量網路: 擁有源點和匯點且每條邊都有殘留容量的網路。殘量網路 \(=\) 容量網路 \(−\) 流量網路。(表示了分配了一定的水流量後還能繼續承受的水流量路線圖)
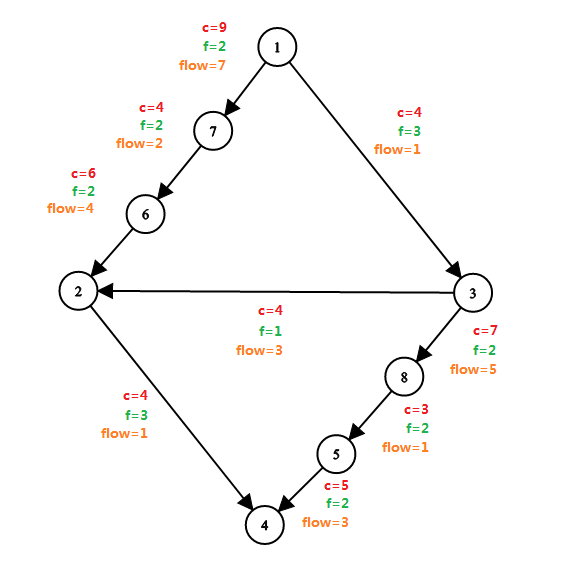
關於流量,容量,殘留容量的理解見下圖:
(用 \(c\) 表示容量,\(f\) 表示流量,\(flow\) 表示殘留容量)
三大性質
- 容量限制:\(\forall (x,y)\in E,f(x,y)\le c(x,y)\)
(如果水流量超過了水管規格就爆了呀)
- 流量守恆:\(\forall (x,y)\in V且x\ne S且x\ne T, {\textstyle \sum_{(u,x)\in E}^{}} f(u,x)={\textstyle \sum_{(x,v)\in E}^{}} f(x,v)\)
(對於所有的水管交界處,有多少水流量過來,就應有多少水流量出去,保證水管質量良好不會洩露並且不會無中生有)
- 斜對稱性:\(\forall (x,y)\in E,f(y,x)=-f(x,y)\)
(可以暫且感性理解為向量的正負。在網路流問題中,這是非常重要的一個性質)
最大流
概念補充
-
網路的流量: 在某種方案下形成的流量網路中匯點接收到的流量值。(小區最終接收到的總水流量)
-
最大流: 網路的流量的最大值。(小區最多可接受到的水流量)
-
最大流網路: 達到最大流的流量網路。(使得小區接收到最多水流量的分配方案路線圖)
增廣路演算法(\(EK\))
概念補充
-
增廣路 \((Augmenting Path)\): 一條在殘量網路中從 \(S\) 到 \(T\) 的路徑,路徑上所有邊的殘留容量都為正。(可以成功從水廠將水送到小區的一條路線)
-
增廣路定理 \((Augmenting Path Theorem)\): 流量網路達到最大流當且僅當殘量網路中沒有增廣路。(無法再找到一路線使得小區獲得更多的流量了)
-
增廣路方法 \((Ford−Fulkerson)\): 不斷地在殘量網路中找出一條從 \(S\) 到 \(T\) 的增廣路,然後根據木桶定律向匯點傳送流量並修改路徑上的所有邊的殘留容量,直到無法找到增廣路為止。該方法的基礎為增廣路定理,簡稱 \(FF\) 方法。(如果有一條路徑可以將水運到小區裡就執行,直到無法再運送時終止)
-
增廣路演算法 \((Edmonds−Karp)\): 基於增廣路方法的一種演算法,核心為 \(bfs\) 找最短增廣路,並按照 \(FF\) 方法執行操作。增廣路演算法的出現使得最大流問題被成功解決,簡稱 \(EK\) 演算法。
演算法流程
下面對 \(EK\) 演算法作詳細介紹。
\(1\) . 用 \(bfs\) 找到任意一條經過邊數最少的最短增廣路,並記錄路徑上各邊殘留容量的最小值 \(cyf\)(殘 \(c\) 餘 \(y\) \(flow\))。 (木桶定律。眾多水管一個也不能爆,如果讓最小的剛好不會爆,其它的也就安全了)
\(2\) . 根據 \(cyf\) 更新路徑上邊及其反向邊的殘留容量值。答案(最大流)加上 \(cyf\)。
\(3\) . 重複 \(1,2\) 直至找不到增廣路為止。
對於 \(2.\) 中的更新操作,利用連結串列的特性,從 \(2\) 開始儲存,那麼 \(3\) 與 \(2\) 就互為一對反向邊,\(5\) 與 \(4\) 也互為一對反向邊 \(\dots\).
只需要記錄增廣路上的每一條邊在連結串列中的位置下標,然後取出來之後用下標對 \(1\) 取異或就能快速得到它的反向邊。
理解
關於建圖:
在具體實現中,由於增廣路是在殘量網路中跑的,所以只需要用一個變數 \(flow\) 記錄殘留容量就足夠了,容量和流量一般不記錄。
為了保證演算法的最優性(即網路的流量要最大),可能在為某一條邊分配了流量後需要反悔,所以要建反向邊。在原圖中,正向邊的殘留容量初始化為容量,反向邊的殘留容量初始化為 \(0\)(可理解為反向邊容量為 \(0\) )。
當我們將邊 \((x,y)\)(在原圖中可能為正向也可能為反向)的殘留容量 \(flow\) 用去了 \(F\) 時,其流量增加了 \(F\),殘留容量 \(flow\) 應減少 \(F\)。根據斜對稱性,它的反邊 \((y,x)\)
流量增加了 \(−F\),殘留容量 \(flow′\) 應減去 \(−F\)(即加上 \(F\))。
那麼如果在以後找增廣路時選擇了這一條邊,就等價於:將之前流出去的流量的一部分(或者全部)反悔掉了個頭,跟隨著新的路徑流向了其它地方,而新的路徑上在到達這條邊之前所積蓄的流量 以及 之前掉頭掉剩下的流量 則順著之前的路徑流了下去。
同理,當使用了反向邊 \((y,x)\) 的殘留容量時也應是一樣的操作。
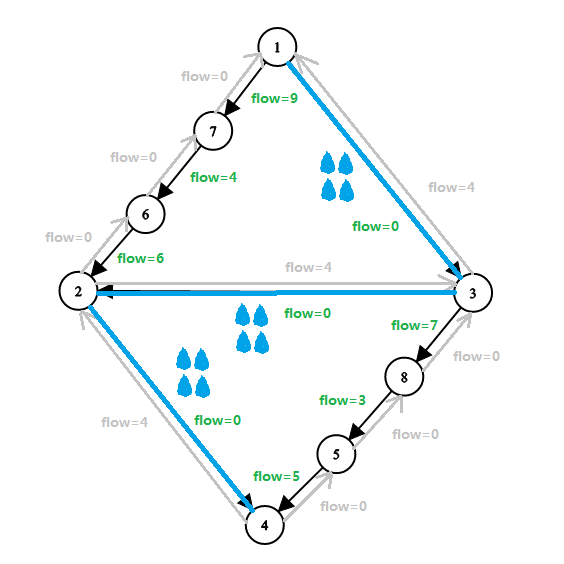
還是之前那個圖,下面是找到了一條最短增廣路 \(1→3→2→4\)(其中三條邊均為黑邊)後的情況:(不再顯示容量和流量,用 \(flow\) 表示殘留容量,灰色邊表示原圖上的反向邊,藍色小水滴表示水流量)
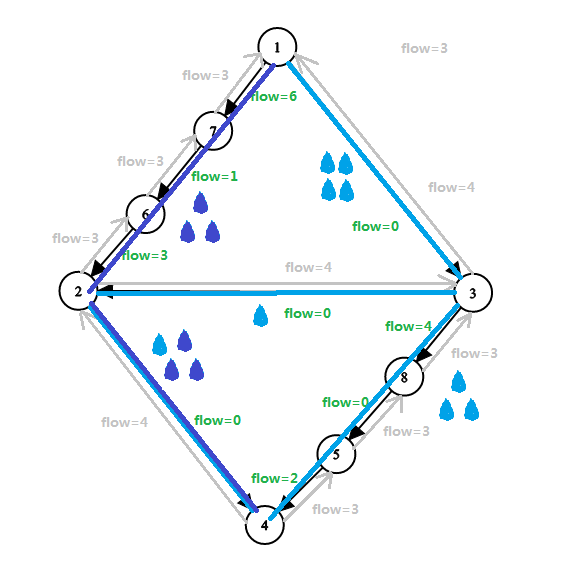
然後是第二條最短增廣路 \(1→7→6→2⇢3→8→5→4\)(其中 \(f(2,3)\) 為灰邊,其餘均為黑邊,紫色小水滴表示第二次新增的水流量):
注:由於在大部分題目中都不會直接使用容量和流量,所以通常會直接說某某之間連一條流量為某某的邊,在沒有特別說明的情況下,其要表示的含義就是殘留容量。後面亦不再強調“殘留”,直接使用“流量”。
複雜度
\(O(nm^{2})\)
code
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<queue>
#define Re register int
using namespace std;
const int N=1e4+3,M=1e5+3,inf=2e9;
int x,y,z,o=1,n,m,h,t,st,ed,maxflow,Q[N],cyf[N],pan[N],pre[N],head[N];
struct QAQ{int to,next,flow;}a[M<<1];
inline void in(Re &x){
int f=0;x=0;char c=getchar();
while(c<'0'||c>'9')f|=c=='-',c=getchar();
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
x=f?-x:x;
}
inline void add(Re x,Re y,Re z){a[++o].flow=z,a[o].to=y,a[o].next=head[x],head[x]=o;}
inline int bfs(Re st,Re ed){
for(Re i=0;i<=n;++i)pan[i]=0;
h=1,t=0,pan[st]=1,Q[++t]=st,cyf[st]=inf;//注意起點cfy的初始化
while(h<=t){
Re x=Q[h++];
for(Re i=head[x],to;i;i=a[i].next)
if(a[i].flow&&!pan[to=a[i].to]){//增廣路上的每條邊殘留容量均為正
cyf[to]=min(cyf[x],a[i].flow);
//用cyf[x]表示找到的路徑上從S到x途徑邊殘留容量最小值
Q[++t]=to,pre[to]=i,pan[to]=1;//記錄選擇的邊在連結串列中的下標
if(to==ed)return 1;//如果達到終點,說明最短增廣路已找到,結束bfs
}
}
return 0;
}
inline void EK(Re st,Re ed){
while(bfs(st,ed)==1){
Re x=ed;maxflow+=cyf[ed];//cyf[ed]即為當前路徑上邊殘留容量最小值
while(x!=st){//從終點開始一直更新到起點
Re i=pre[x];
a[i].flow-=cyf[ed];
a[i^1].flow+=cyf[ed];
x=a[i^1].to;//連結串列特性,反向邊指向的地方就是當前位置的父親
}
}
}
int main(){
in(n),in(m),in(st),in(ed);
while(m--)in(x),in(y),in(z),add(x,y,z),add(y,x,0);
EK(st,ed);
printf("%d",maxflow);
}
\(Dinic\)
在 \(EK\) 演算法中,每一次 \(bfs\) 最壞可能會遍歷整個殘量網路,但都只會找出一條最短增廣路。
那麼如果一次 \(bfs\) 能夠找到多條最短增廣路,速度就上去了。
\(Dinic\) 演算法便提供了該思路的一種實現方法。
網路流的演算法多且雜,對於初學者來說,在保證效率的前提下最佳化 \(Dinic\) 應該是最好寫的一種了。
演算法流程
\(1\) . 根據 \(bfs\) 的特性,找到 \(S\) 到每個點的最短路徑(經過最少的邊的路徑),根據路徑長度對殘量網路進行分層,給每個節點都給予一個層次,得到一張分層圖。
\(2\) . 根據層次反覆 \(dfs\) 遍歷殘量網路,一次 \(dfs\) 找到一條增廣路並更新,直至跑完能以當前層次到達 \(T\) 的所有路徑。
多路增廣
可以發現,一次 \(bfs\) 會找到 \([1,m]\) 條增廣路,大大減少了 \(bfs\) 次數,但 \(dfs\) 更新路徑上的資訊仍是在一條一條地進行,效率相較於 \(EK\) 並沒有多大變化。
為了做到真正地多路增廣,還需要進行最佳化。
在 \(dfs\) 時對於每一個點 \(x\),記錄一下 \(x⇝T\) 的路徑上往後走已經用掉的流量,如果已經達到可用的上限則不再遍歷 \(x\) 的其他邊,返回在 \(x\) 這裡往後所用掉的流量,回溯更新 \(S⇝x\) 上的資訊。
如果到達匯點則返回收到的流量,回溯更新 \(S⇝T\) 上的資訊。
弧最佳化
原理:
在一個分層圖當中,\(\forall x\in V\),任意一條從 \(x\) 出發處理結束的邊(弧),都成了 “廢邊”,在下一次到達 \(x\) 時不會再次使用。(水管空間已經被榨乾淨了,無法再透過更多的水流,直接跳過對這些邊的無用遍歷)
實現方法:
用陣列 ¥cur_{x}$ 表示上一次處理 \(x\) 時遍歷的最後一條邊(即 \(x\) 的當前弧),其使用方法與連結串列中的 \(head\) 相同,只是 \(cur\) 會隨著圖的遍歷不斷更新。由於大前提是在一個分層圖當中,所以每一次 \(bfs\) 分層後都要將 \(cur\) 初始化成 \(head\) 。
特別的,在稠密圖中最能體現當前弧最佳化的強大。
複雜度
\(O(n^{2}m)\)
code
bool bfs(){
memset(d,0,sizeof(d));
queue<int >q;
q.push(1);
d[1]=1;
while(q.size()){
int u=q.front();
q.pop();
for(int i=head[u];i;i=ad[i].nxt){
int v=ad[i].v,w=ad[i].w;
if(d[v]||!w){
continue;
}
q.push(v);
d[v]=d[u]+1;
if(v==f+n+n+dr+2)return 1;
}
}
return 0;
}
int dfs(int u,int flow){
if(u==n+n+f+dr+2)return flow;
int rest=flow,tot=0;
for(int i=head[u];i;i=ad[i].nxt){
int v=ad[i].v,w=ad[i].w;
if((!w)||d[u]+1!=d[v])continue;
int k=dfs(v,min(w,rest));
rest-=k;
tot+=k;
ad[i].w-=k;
ad[i^1].w+=k;
}
return tot;
}
void dinic(){
while(bfs())max_f+=dfs(1,0x7fffffff);
}
一道例題
[USACO07OPEN] Dining G
網路最大瘤解決二分圖匹配的連邊思路:
\(s→left→right→t\)
這道題貌似是個“三分圖”最大“匹配”(注意這裡加了引號)。
可以將食物、牛、飲料分別定義為:左部點,中部點,右部點。
但是這裡的“匹配”就不是原來的匹配了。
匹配本來的意思是:任意兩邊不共端點。
而在這裡,“匹配”的意思任意兩條從左部到右部的路徑沒有公共點。
但是建圖的方式還是可以仿照二分圖最大匹配的——
\(s→left→mid→right→t\)
但是這樣一來,如果您真正理解了網路最大瘤做二分圖最大匹配的原理時,你就會發現:
本來經過所有點的流量都應該小於等於1,但是在這裡經過mid點的流量可能會大於1!這樣一來,就會出現一個問題:有兩條路徑共mid點,與我們之前談到的“三分圖”最大“匹配”的定義不符。
這說明我們需要對mid點進行“限流”(沒錯,一開始我就是把這個東西稱為“限流”,後面才知道叫拆點)
限流的方法很簡單:在《挑戰程式設計競賽——第二版》的第3章第5節,214頁第二點有提到:
將一個點拆做入點和出點,連一條權值為限制流量的邊。
所以就可以這樣建圖:
\(s→left→mid→mid →right→t\)
然後跑 \(Dinic\) 即可(雖說看起來 \(EK\) 可過)。
最小割
1.概念
-
網路的割集\((Network Cut Set)\) : 把一個源點為 \(S\),匯點為 \(T\) 的網路中的所有點劃分成兩個點集 \(s\) 和 \(t\),\(S\in s,T\in t\),由 \(x\in s\) 連向 \(y\in t\) 的邊的集合稱為割集。可簡單理解為:對於一個源點為 \(S\),匯點為 \(T\) 的網路,若刪除一個邊集 \(E′\subseteq E\) 後可以使 \(S\) 與 \(T\) 不連通,則成 \(E′\) 為該網路的一個割集。(有壞人不想讓小區通水,用鋸子割掉了一些邊)
-
最小割 \((Minimum Cut)\) : 在一個網路中,使得邊容量之和最小的割集。(水管越大越難割,壞人想要最節省力氣的方案)
-
最大流最小割定理:$(Maximum Flow Minimum Cut Theorem) $:任意一個網路中的最大流等於最小割
費用流
概念
每條邊在容量 \(c\) 的基礎上還有費用 \(w\),表示在這條邊每流單位流量需要支付 \(w\) 的代價,由此可以定義最小費用最大流。
\(EK\)
只需將最大流 \(EK\) 演算法中的流程 \(1\) “ \(bfs\) 找到任意一條最短增廣路 ” 改為 “ \(Spfa\) 找到任意一條單位費用之和最小的增廣路 ”,即可得到最小費用最大流。
特別的,為了提供反悔機會,原圖中 \(\forall (x,y)\in E\) 的反向邊單位費用應為 \(−w(x,y)\) 。為什麼不用 \(dijkstra\)?原因就在這裡啊!)
#include<algorithm>
#include<cstdio>
#include<queue>
#define LL long long
#define Re register int
using namespace std;
const int N=5003,M=5e4+3,inf=2e9;
int x,y,z,w,o=1,n,m,h,t,st,ed,cyf[N],pan[N],pre[N],dis[N],head[N];LL mincost,maxflow;
struct QAQ{int w,to,next,flow;}a[M<<1];queue<int>Q;
inline void in(Re &x){
int f=0;x=0;char c=getchar();
while(c<'0'||c>'9')f|=c=='-',c=getchar();
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
x=f?-x:x;
}
inline void add(Re x,Re y,Re z,Re w){a[++o].flow=z,a[o].w=w,a[o].to=y,a[o].next=head[x],head[x]=o;}
inline void add_(Re a,Re b,Re flow,Re w){add(a,b,flow,w),add(b,a,0,-w);}
inline int SPFA(Re st,Re ed){
for(Re i=0;i<=ed;++i)dis[i]=inf,pan[i]=0;
Q.push(st),pan[st]=1,dis[st]=0,cyf[st]=inf;
while(!Q.empty()){
Re x=Q.front();Q.pop();pan[x]=0;
for(Re i=head[x],to;i;i=a[i].next)
if(a[i].flow&&dis[to=a[i].to]>dis[x]+a[i].w){
dis[to]=dis[x]+a[i].w,pre[to]=i;
cyf[to]=min(cyf[x],a[i].flow);
if(!pan[to])pan[to]=1,Q.push(to);
}
}
return dis[ed]!=inf;
}
inline void EK(Re st,Re ed){
while(SPFA(st,ed)){
Re x=ed;maxflow+=cyf[ed],mincost+=(LL)cyf[ed]*dis[ed];
while(x!=st){//和最大流一樣的更新
Re i=pre[x];
a[i].flow-=cyf[ed];
a[i^1].flow+=cyf[ed];
x=a[i^1].to;
}
}
}
int main(){
in(n),in(m),in(st),in(ed);
while(m--)in(x),in(y),in(z),in(w),add_(x,y,z,w);
EK(st,ed);
printf("%lld %lld",maxflow,mincost);
}