並查集的一些基本概念以及基本操作(初始化,合併,查詢等操作)

首先要明白的是為什麼會有並查集這種資料結構的出現,我們知道,對於一些比較常見的實際問題,舉個簡單的例子
比如說,我們要在一個無重複資料的陣列中尋找一個指定的元素,那麼最簡單的方法就是直接for迴圈一遍暴力查詢即可

時間複雜度為O(n),花費時間為線性時間,而現在如果我們把這個常規問題抽象化,即

在一些有N個元素的集合應用問題中，我們通常是在開始時讓每個元素構成一個單元素的集合，然後按一定順序將屬於同一組的元素所在的集合合併，其間要反覆查詢一個元素在哪個集合中。

這樣的問題看起來似乎很簡單，每次直接暴力查詢即可，但是我們需要注意的問題是，在資料量非常大的情況下，那麼時間複雜度將達到O（N*n）(n為查詢次數)，那麼這類問題在實際應用中，如果採取上述方法去做的話，耗費的時間將是巨大的。而如果用常規的資料結構去解決該類問題的話（順序結構，普通樹結構等），那麼計算機在空間上也無法承受。所以，並查集這種資料結構便應運而生了。

1.並查集的基本概念：

首先我們要給並查集下一個比較確切的概念：

下面是百度百科給並查集下的概念：

並查集是一種樹型的資料結構，用於處理一些不相交集合（Disjoint Sets）的合併及查詢問題。常常在使用中以森林來表示。集就是讓每個元素構成一個單元素的集合，也就是按一定順序將屬於同一組的元素所在的集合合併。

2.並查集的一些基本操作：

瞭解了並查集的一些基本概念之後，那麼必然涉及到並查集的一些基本操作（就像我們一開始學習連結串列這種資料結構時，在瞭解了基本概念之後，都會涉及到該種資料結構的一些基本操作），下面是並查集的幾種基本操作：

1.MAKE-SET(x)：即初始化操作，建立一個只包含元素 x 的集合。

通常並查集初始化操作是對每個元素都建立一個只包含該元素的集合。這意味著每個成員都是自身所在集合的代表，所以我們只需要將所有成員的父結點設為它自己就好了。

2.UNION(x, y)：即合併操作，將包含 x 和 y 的集合合併為一個新的集合。

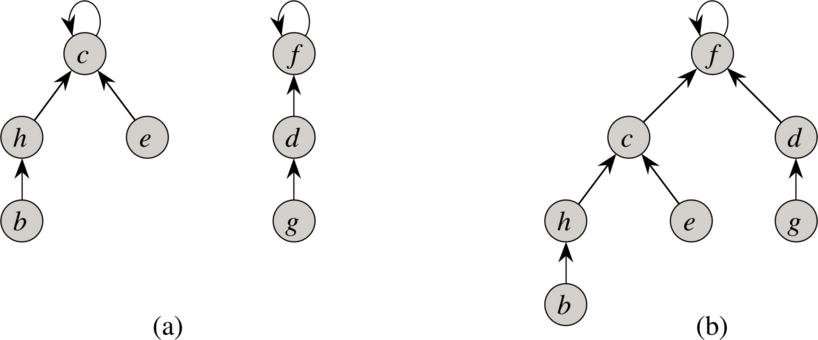
並查集的合併操作需要用到查詢操作的結果。合併兩個元素所在的集合，需要首先求出兩個元素所在集合的代表元素，也就是結點所在有根樹的根結點。接下來將其中一個根結點的父親設定為另一個根結點。這樣我們就把兩棵有根樹合併成一棵了。

如上圖所示，圖（a）為兩個合併前的集合對應的不相交森林，兩個集合對應的有根樹的根分別是 c 和 f。我們將兩個集合進行合併，就會得到圖（b）所示的新集合，集合對應的有根樹的根為 f。

3.FIND-SET(x)：即查詢操作，計算 x 所在的集合。

在不相交森林中，並查集的查詢操作，指的是查詢出指定元素所在有根樹的根結點是誰。我們可以通過每個指向父結點的邊回溯到結點所在有根樹的根，也就是對應集合的代表元素。

並查集的查詢操作最壞情況下的時間複雜度為O(n),其中 n 為總元素個數。最壞情況發生時，每次合併對應到森林上都是一個點連到一條鏈的一端。此時如果每次都查詢鏈的最底端，也就是最遠離根的位置的元素時，複雜度便是O(n)了。

為了改善時間效率，可以通過啟發式合併方法，將包含較少結點的樹接到包含較多結點的樹根上，可以防止樹退化成一條鏈。另外，我們也可以通過路徑壓縮的方法來進一步減少均攤複雜度。同時使用這兩種優化方法，可以將每次操作的時間複雜度優化至接近常數級。

3.並查集森林：

通常我們會用有根樹來表示集合，樹中的每一個結點都對應集合的一個成員，每棵樹表示一個集合。

每個成員都有一條指向父結點的邊，整個有根樹通過這些指向父結點的邊來維護。每棵樹的根就是這個集合的代表，並且這個代表的父結點是它自己。

通過這樣的表示方法，我們將不相交的集合轉化為一個森林，也叫不相交森林。

根據上面對並查集的描述，那麼我們能夠得到一些並查集的性質：
1.通常我們用森林來表示並查集，一棵有根樹表示一個集合

2.如果 a 和 b 屬於一個集合，b 和 c 屬於一個集合，（a和b 以及 b和c同屬的集合屬於不相交集合,即這兩個集合要麼是同一個集合,要麼這兩個集合相交部分為空）,則 a 和 c 也屬於一個集合

3.不加優化的並查集，最壞情況下查詢的時間複雜度為O（n）

那麼在有了以上的敘述之後，我們就要著手實現程式碼了：

首先我們先要宣告兩個陣列，分別用於記錄當前操作節點的父親節點和作為根節點時整棵樹的大小(也叫樹的秩):

#define size 101
int father[size],rank[size];

在儲存結構確定了之後，那麼我們則要對每個節點的父親節點初始化並且賦予秩的值：

//並查集初始化操作
void Init(int N){
    int i;
    for(i = 1;i < N;++i){
        father[i] = i;
        rank[i] = 1;        //father[i]用於記錄節點i的父親節點,而rank[i]則用於記錄
                            //節點i作為根節點時整棵樹的大小(也稱權重,用於記錄樹的節點個數)
    }
}

那麼當初始化操作確定之後，我們要做的就是查詢和合並操作了，如果待查詢的兩個資料中集合的代表資料（即樹的根）不是同一個的話，那麼我們則需要將這兩個集合合併成一個（即將兩棵有根樹合併成一棵有根樹，這樣的話方便後續資料的查詢），而合併操作則要涉及到怎麼樣將兩棵樹合併才能使得後序的查詢操作遍歷樹節點的次數儘量少？那麼這裡就涉及到了這兩個集合中代表元素的權重問題了。

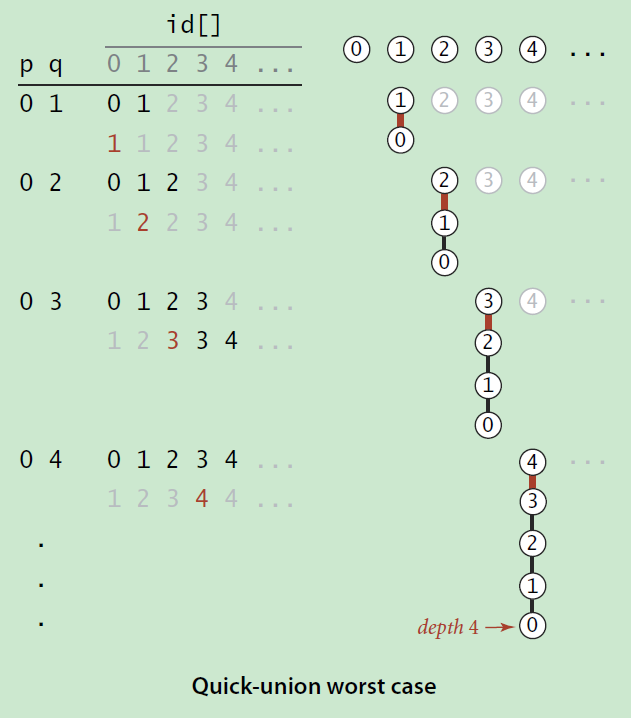
首先我們分析，如果不對兩棵有根樹的權重加以判斷，而是隨意連線兩棵樹的根，將其合併成一棵有根樹，那麼在最壞的情況下，最後n個元素合併之後，樹結構可能會退化成了鏈結構：

圖片來自《演算法》（第四版）
如上圖所示，這樣的話在後續查詢操作中，查詢操作的最壞時間複雜度則依然還是線性複雜度O（n）

O(

那麼為了防止這樣的問題出現，我們則需要在每次合併操作時，判斷兩棵樹根節點的權重，然後再將權重小的根節點指向權重大的根節點（即將小樹指向大樹）

原因其實很簡單：當把小樹接至大樹上時，那麼大樹上的節點尋找根節點的操作次數不變，而小樹上的節點尋找根節點的操作次數各加1即可。那麼總的增加的次數即為小樹的節點數。

而如果反過來，把大樹接至小樹上時，那麼小樹上的節點尋找根節點的操作次數不變，而大樹上的節點尋找根節點的操作次數各加1，那麼總的增加的次數即為大樹的節點數。

根據以上分析，為了儘量增加尋找根節點時的查詢效率，那麼顯然是將權重小的根節點指向權重大的根節點（即將小樹指向大樹）

有了這樣的分析之後，那麼我們就可以將查詢和合並操作封裝成兩個完整的函式：

//並查集的查詢操作,查詢當前操作到的節點的根節點
//在查詢操作中,我們需要將查詢的過程壓縮,即減少向上遍歷詢問次數
//那麼一般情況下會採取路徑壓縮的做法
//路徑壓縮：就是在每次查詢時，令查詢路徑上的每個節點都直接指向根節點

int find_set(int node){
    while(father[node] != node){
        node = father[node];
    }
    return node;
}

//並查集的合併操作,將兩個不相交的集合合併成一個,即將兩棵不同的有根樹
//通過小樹的根節點指向大樹的根節點,使得兩棵有根樹合併成合一課有根樹

int _union(int p,int q){
    int root1 = find_set(p);
    int root2 = find_set(q);
    if(root1==root2){
        return 0;     //如果當前操作到的兩個節點同屬於一個連通分量(即是同一棵樹中的節點)
                    //則不執行合併操作直接返回0,表示合併失敗
    }
    if(rank[root1] > rank[root2]){
        father[root2] = root1;         //小樹連線到大樹上,並且權值加至合併後
                                      //整棵完整的樹的樹根上
        rank[root1] += rank[root2];
    }
    else{
        father[root1] = root2;
        rank[root2] += rank[root1];
    }
    return 1;
}

但是我們仔細想想，既然前面已經做了按秩合併的優化，那麼是否這就是演算法的最佳優化效果呢？

我們試著看一下這張圖：

首先我們考慮，如果我們操作到的元素為a和b，那麼a找到根節點需要的操作次數為(n-1)次，b找到根節點需要的操作次數為(n-2)次,

那麼當節點數比較多的時候，尋找根節點的過程是可以再壓縮的，我們可以這樣想，a,b,c,d...乃至後面所有的節點（包括根節點）,在執行查詢的過程中，都是為了找到自己所屬的這個集合中的代表元素(也就是根節點)，那麼除了根節點以外的節點，在這個時候是沒有主次之分，也沒有像二叉樹那樣嚴格區分左右子樹的行為，所以呢，我們為了提高查詢根節點的效率，我們可以簡化查詢操作，將根節點以外的所有節點都直接接在根節點的後面，這樣的話能將查詢的時間均攤，並且使得演算法的效率接近常數級。

這種操作我們叫做路徑壓縮操作，具體實現我們可以在查詢的過程中，便查詢邊壓縮，如果待操作節點不是根節點，那麼就將其接至根節點的後面。我們可以用遞迴操作(注意棧溢位的問題)和非遞迴操作實現：

遞迴操作：

int find_set(int node) {
    if (father[node] != node) {
        father[node] = find_set(father[node]);   //在 find_set 函式中,當前結點不是根結點的情況下,
                                                 //將遞迴的結果賦值為當前結點的父節點,而遞迴結束的條件是
    }                                            //找到根節點,即if迴圈不成立的時候,遞迴結束,返回根節點至上一層呼叫該
    return father[node];                         //函式的地方,然後將上一層函式節點的父親節點賦值為根節點
                                                //隨後重複上述操作,將"父親節點(根節點)"帶回上一層函式並賦值,直到最外層呼叫遞迴的函式
                                                //該函式將"父親節點(根節點)"返回至_union函式
}

非遞迴操作（我們要先找到根節點，並將途經的節點一一儲存起來,然後再重新遍歷一次將途經節點的父節點均賦值為根節點）：

/*  非遞迴方法,使用迭代的方式尋找根節點
 *  需遍歷兩次節點(重複操作較多)
 */
int find_set(int node)
{
	//如果是直接孩子或樹根，則直接返回樹根
	if (father[node] == node)
		return father[node];

	int rec[size], root, k = 0;
	//退出迴圈時即找到了樹根i，因為此時father[i] == i;
	//查詢路徑上的結點已經儲存到rec陣列，樹根儲存為root
	for (; father[node] != node; node = father[node])
		rec[k++] = node;
	root = node;     //根節點
	//陣列中的元素其父親全部設定為root
	int i = 0;
	for (; i != k; i++)
		father[rec[i]] = root;
	return root;
}

因此經過以上 按秩合併操作和路徑壓縮優化後，則實現的完整程式碼如下（C語言實現）：

#include<stdio.h>
#define size 101

int father[size],rank[size];

//並查集初始化操作
void Init(int N){
    int i;
    for(i = 1;i < N;++i){
        father[i] = i;
        rank[i] = 1;        //father[i]用於記錄節點i的父親節點,而rank[i]則用於記錄
                            //節點i作為根節點時整棵樹的大小(也稱權重,用於記錄樹的節點個數)
    }
}

//並查集的查詢操作,查詢當前操作到的節點的根節點
//在查詢操作中,我們需要將查詢的過程壓縮,即減少向上遍歷詢問次數
//那麼一般情況下會採取路徑壓縮的做法
//路徑壓縮：就是在每次查詢時，令查詢路徑上的每個節點都直接指向根節點

int find_set(int node) {
    if (father[node] != node) {
        father[node] = find_set(father[node]);   //在 find_set 函式中,當前結點不是根結點的情況下,
                                                 //將遞迴的結果賦值為當前結點的父節點,而遞迴結束的條件是
    }                                            //找到根節點,即if迴圈不成立的時候,遞迴結束,返回根節點至上一層呼叫該
    return father[node];                         //函式的地方,然後將上一層函式節點的父親節點賦值為根節點
                                                //隨後重複上述操作,將"父親節點(根節點)"帶回上一層函式並賦值,直到最外層呼叫遞迴的函式
                                                //該函式將"父親節點(根節點)"返回至_union函式
}

//並查集的合併操作,將兩個不相交的集合合併成一個,即將兩棵不同的有根樹
//通過小樹的根節點指向大樹的根節點,使得兩棵有根樹合併成合一課有根樹

int _union(int p,int q){
    int root1 = find_set(p);
    int root2 = find_set(q);
    if(root1==root2){
        return 0;     //如果當前操作到的兩個節點同屬於一個連通分量(即是同一棵樹中的節點)
                    //則不執行合併操作直接返回0,表示合併失敗
    }
    if(rank[root1] > rank[root2]){
        father[root2] = root1;         //小樹連線到大樹上,並且權值加至合併後
                                      //整棵完整的樹的樹根上
        rank[root1] += rank[root2];
    }
    else{
        father[root1] = root2;
        rank[root2] += rank[root1];
    }
    return 1;
}

int main(){
    int i, m, x, y;
    Init(size);        //初始化操作
    scanf("%d",&m);    //m表示操作次數
    for (i = 0; i < m; ++i) {
        scanf("%d %d",&x,&y);
        int ans = _union(x, y);
        if (ans) {
            printf("success\n");
        }
        else {
            printf("failed\n");
        }
    }
    return 0;
}

C++語言實現：

#include <iostream>
#include<algorithm>
using namespace std;

class DisjointSet {
private:
    int *father, *rank;
public:
    DisjointSet(int size) {
        father = new int[size];
        rank = new int[size];
        for (int i = 0; i < size; ++i) {
            father[i] = i;
            rank[i] = 0;
        }
    }
    ~DisjointSet() {
        delete[] father;
        delete[] rank;
    }
    int find_set(int node) {
        if (father[node] != node) {
            father[node] = find_set(father[node]);
        }
        return father[node];
    }
    bool merge(int node1, int node2) {
        int ancestor1 = find_set(node1);
        int ancestor2 = find_set(node2);
        if (ancestor1 != ancestor2) {
            if (rank[ancestor1] > rank[ancestor2]) {
                swap(ancestor1, ancestor2);
            }
            father[ancestor1] = ancestor2;
            rank[ancestor2] = max(rank[ancestor1] + 1, rank[ancestor2]);
            return true;
        }
        return false;
    }
};

int main() {
    DisjointSet dsu(100);
    int m, x, y;
    cin >> m;
    for (int i = 0; i < m; ++i) {
        cin >> x >> y;
        bool ans = dsu.merge(x, y);
        if (ans) {
            cout << "success" << endl;
        } else {
            cout << "failed" << endl;
        }
    }
    return 0;
}

效果圖：

總結：並查集演算法涉及到很多演算法優化的思想，需要多練習熟悉，並且要深入理解並查集演算法。

除了學校oj外，另外還有一些並查集的題目可以試著做一做：

poj 2542    poj1182（較難，可仔細琢磨）

POJ 1308 1456 1611 1703 1733 1984 1986(LCA Tarjan演算法 + 並查集) 1988 2236 2492 2524。

HDU 3038

如有錯誤，還請指正，O(∩_∩)O謝謝