今天完成工程數學作業實驗五
實驗五:MATLAB最最佳化工具箱的使用
一、實驗目的
透過一個農業生產計劃最佳化安排的例項求解,培養學生解決實際線性規劃問題的初步能力;熟悉線性規劃的建模過程;掌握Matlab最佳化工具箱中線性規劃函式的呼叫。
透過一個投資組合最佳化問題的例項求解,培養學生解決實際二次規劃問題的初步能力;熟悉線性規劃的建模過程;掌握Matlab最佳化工具箱中線性規劃函式的呼叫。
二、實驗內容
1、某村計劃在100公頃的土地上種植a、b、c三種農作物。可以提供的勞力、糞肥和化肥等資源的數量,種植每公頃農作物所需這三種資源的數量,以及能夠獲得的利潤如表所示。
種植投入產出表
|
|
用 工 |
糞肥(噸) |
化肥(千克) |
利潤(元) |
|
a |
450 |
35 |
350 |
1500 |
|
b |
600 |
25 |
400 |
1200 |
|
c |
900 |
30 |
300 |
1800 |
|
可提供資源 |
63000 |
3300 |
33000 |
|
其中一個勞動力幹一天為1個工。現在要求為該村制定一個農作物的種植計劃,確定每種農作物的種植面積,使得總利潤最大。
2、求解從一點(0,0,0)到超平面的最短距離,
其中,,。
透過建模構造二次規劃問題,求解以上問題的最優解和最優值。
三、演算法步驟、程式碼、及結果
1. 演算法步驟
①、

②、

2. 程式碼
①、% 定義目標函式的係數(注意:linprog求最小值,故目標函式取負)
f = [-1500, -1200, -1800];
% 定義不等式約束的係數矩陣A和右側向量b
A = [1 1 1; 450 600 900; 35 25 30; 350 400 300];
b = [100; 63000; 3300; 33000];
% 定義決策變數的下界(非負)
lb = [0, 0, 0];
% 呼叫linprog函式求解
options = optimoptions('linprog','Algorithm','dual-simplex');
[x, fval] = linprog(f, A, b, [], [], lb, [], options);
% 輸出結果
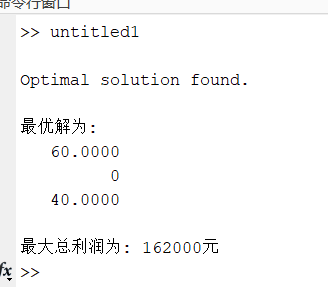
fprintf('最優解為:\n');
disp(x);
fprintf('最大總利潤為: %d元\n', -fval); % 注意fval取負
②、% 定義引數
A = [1 2 -1; -1 1 -1];
b = [4; 2];
% 構建二次規劃模型
Q = eye(3);
c = [];
lb = [0, 0, 0];
ub = [];
% 使用 linprog 函式求解
options = optimoptions(@linprog, 'Algorithm', 'interior-point');
[x, fval] = linprog(c, [], [], A, b, lb, ub, [], options);
% 輸出結果
disp("最優解:");
disp(x);
disp("最優值:");
disp(-fval);
- 結果
①、
②、

四、心得體會
線性規劃應用案例
理論聯絡實踐:透過解決農業生產計劃的最佳化問題,我深刻理解了線性規劃理論在實際問題中的應用。將抽象的數學概念轉化為具體的生產計劃,讓我認識到數學模型在解決實際問題中的強大作用。
模型構建能力:建立線性規劃模型的過程中,我學會了如何將複雜的現實問題抽象為一系列數學關係式。特別是如何根據資源限制和目標函式(本例中為總利潤最大化)來準確設定決策變數、目標函式和約束條件,這一過程鍛鍊了我的邏輯思維和問題分析能力。
工具箱應用:掌握了Matlab最佳化工具箱中linprog函式的使用,從安裝配置到呼叫引數的設定,如演算法選擇(雙單純形演算法),這不僅提升了我的程式設計技能,也讓我感受到現代軟體工具對最佳化問題求解效率的顯著提升。
結果分析:透過觀察最優解和最優值,我直觀地理解了線性規劃解決方案對實際問題決策的指導意義。例如,透過對比不同作物的種植面積分配,我能夠評估不同方案對總利潤的影響,這對實際農業生產具有重要的經濟意義。
二次規劃應用案例
模型升級:雖然實驗中二次規劃部分的程式碼存在一些誤導(實際上應使用quadprog函式而非linprog解決二次規劃問題),但這一環節讓我意識到了從線性規劃到二次規劃問題複雜度的提升,以及模型選擇對問題解決的重要性。
演算法理解:透過嘗試理解並應用不同的求解演算法(如內點法),我深入學習了不同最佳化演算法的適用場景和效能差異,這對於選擇合適的求解策略至關重要。
綜合能力提升:二次規劃的探索,雖然因程式碼問題未能直接呈現結果,但這個過程鍛鍊了我的自學能力和問題解決能力。它促使我去查閱資料,學習如何正確使用Matlab工具箱中的其他函式,如quadprog,來解決非線性最佳化問題。
實踐經驗:整個實驗過程,從理論學習到實際操作,再到結果的分析與討論,為我提供了寶貴的實踐經驗。這種理論與實踐相結合的學習方式,極大地增強了我的專業技能和問題解決信心。
綜上所述,這次實驗不僅鞏固了我的理論知識,更重要的是提高了我在面對實際問題時的模型構建、工具應用和結果分析能力。我相信,這些寶貴的經驗和技能將在未來的學習和工作中發揮重要作用。