- 因為沒有找到顯示上標的辦法,圖片也會被強制換行,有幾個符號需要給瀏覽器裝一個顯示 latex 公式的外掛才能正常顯示, Math Anywhere for chrome
- 開局一張圖,內容全靠編,本文內容基本是圍繞 圖3 展開的
- 閱讀第1節需要微積分基礎
- 第2節是對第一節內容的逐句翻譯, 程式碼非常囉嗦, 而且時間複雜度是 O(n^4), 對程式碼有潔癖的同學可以按照 1-> 5-> 3 的順序閱讀
- 第3節不需要計算微積分,瞭解概念即可
- 閱讀第5節需要線性代數基礎
- 考慮到矩陣微分比較複雜,且對於理解神經網路不是必須的,放到了比較靠後的位置
- 因為我沒有在別的地方找到以均方差為誤差函式的神經網路實現細節,所以給出了全部的計算細節,如果你算的結果和本文不一致(大機率是我打錯了),請檢視程式碼
- 參考書目是我參考的書,並沒有強烈推薦,淘寶連結是隨機點開的,非廣告。實際上 《MATLAB神經網路應用設計-第2版》 和 《矩陣分析與應用-第1版》 已經停印很久了,並不建議購買
本文主要參考: MIT 6.034, Lecture 12A: Neural Nets (網易的版本少了一課)
神經網路做什麼
神經網路[1]用於根據特徵判斷資料是不是某一類的問題,比如:
| 特徵1 | 特徵2 | 是不是鳥類 |
|---|---|---|
| 有羽毛 | 會飛 | 是 |
| 沒有羽毛 | 不會飛 | 不是 |
| 有羽毛 | 不會飛 | ? |
神經元
神經元模型如下 (圖1):
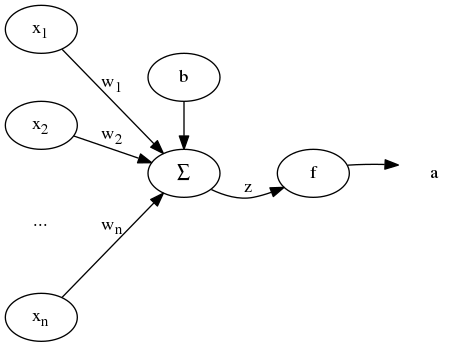
神經元的輸入為 [x1, x2, ..., xn] , 對每一項 xi 乘以權重 wi 以及偏置單元 b 求和得到加權和 z, 透過啟用函式(傳遞函式) f, 得到輸出 f(z) = a。 為了計算簡便, 令 x0 = 1 , w0 = b, 輸出為:
在經典模型中,啟用函式為 sigmoid 函式,其定義及導數如下: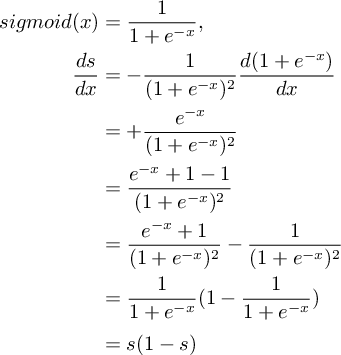
sigmoid 影像如下 (圖2):
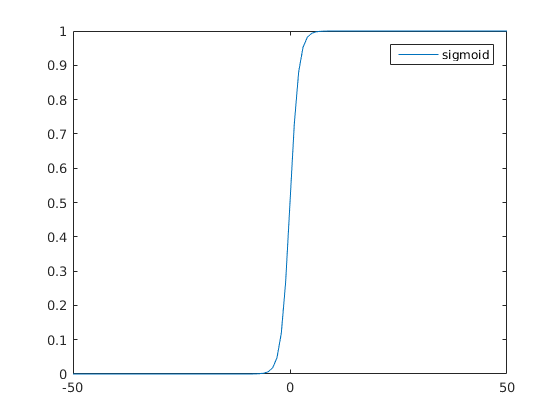
sigmoid 函式的作用是將離散的輸入壓縮為 (0, 1) 之間的連續值,使離散函式可導, 且其導數可以完全用因變數表示,方便計算。
神經網路
多個神經元組成神經網路 (圖3):
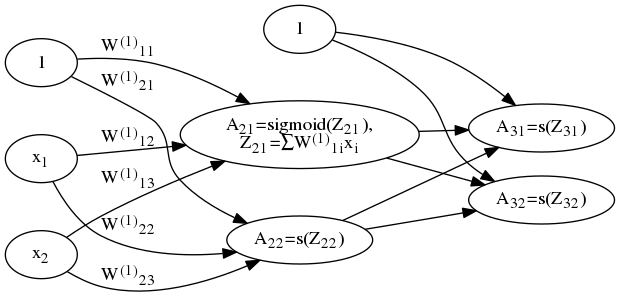
神經網路中第一層稱為輸入層,最後一層稱為輸出層,中間的層稱為隱藏層。 對於圖3所示網路,總共有 3 層,輸入層 L1 = {x1, x2, ..., xn}, 輸出層 L3, 和一個隱藏層 L2。 從第1層到第2層的引數矩陣為 $W^{(1)}$ , 第2層到第3層的引數矩陣為 $W^{(2)}$ 。引數矩陣形式如下:
以上是一個糟糕的例子,看不出 $W^{(l)}$ 的大小,實際上 $W^{(l)}$ 大小為 nl + 1 x (nl + 1) 。
前向傳遞
對於圖3所示網路,考慮一組輸入的情況,記第 l 層 sigmoid 單元的輸入為 $Z^{(l)}$ ,輸出為 $A^{(l)}$ , 由輸入及引數計算輸出: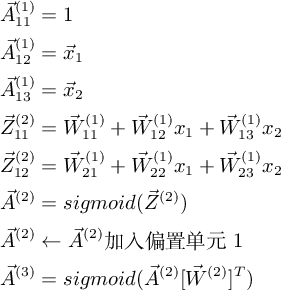
因為計算是從前向後進行的,稱為前向傳遞。
損失函式
定義輸出層輸出 $A^{(3)}$ 和樣本值 y 的均方差為損失函式(代價函式):
考慮結構風險最小化,加入正則化項:
另一個常見的損失函式是由最大似然估計[2]得出的:
反向傳遞
應用鏈式法則[3]從後向前依次求 J 關於 $W^{(2)}, W^{(1)}$ 的偏導[4]的過程稱為反向傳遞(BP)。 因為 BP 的向量化比較複雜,先考慮只有1組輸入的情況下的標量結果,即 X 的大小為 1 x n 。 先計算 J 關於 $W^{(2)}_{12}$ 和 $W^{(1)}_{12}$ 的偏導: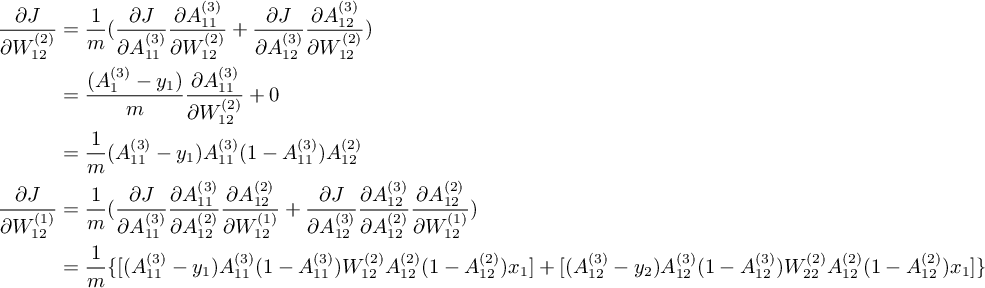
類似地應用鏈式法則,求出全部關於權重的偏導 ( $A^{(2)}_{11} = A^{(1)}_{11} = 1$ ) :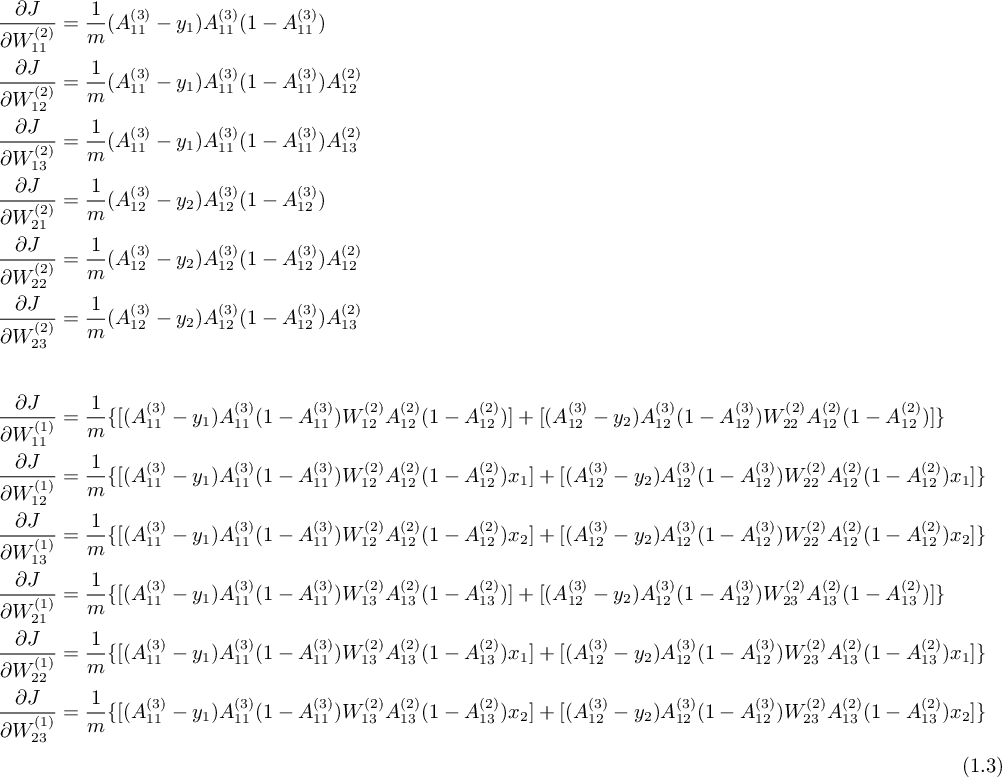
對比上式可以看出,在從後向前逐級計算偏導的過程中,存在著可以重複利用的項,所以(線性)增加層數帶來演算法複雜度的增加是線性的。
正則化項的偏導為:
最後,神經網路的輸出和樣本值接近意味著 J 儘可能小, 利用梯度下降[5]求解最佳化問題 $argmin{J(W)}$ ,計算權重 :
準備資料
以圖3所示網路對經典的 鳶尾花 分類。 原始資料格式如下:
| 萼片長(cm) | 萼片寬(cm) | 花瓣長(cm) | 花瓣寬(cm) | 分類 |
|---|---|---|---|---|
| 5.1 | 3.5 | 1.4 | 0.2 | Iris-setosa |
| 4.9 | 3.0 | 1.4 | 0.2 | Iris-setosa |
| ... | ... | ... | ... | ... |
| 7.0 | 3.2 | 4.7 | 1.4 | Iris-versicolor |
| 6.4 | 3.2 | 4.5 | 1.5 | Iris-versicolor |
| ... | ... | ... | ... | ... |
| 6.3 | 3.3 | 6.0 | 2.5 | Iris-virginica |
| 5.8 | 2.7 | 5.1 | 1.9 | Iris-virginica |
| ... | ... | ... | ... | ... |
資料前4列為特徵值,最後一列為分類,總共有150行, 每50行 為一種鳶尾花(3分類問題)。 因為圖3所示網路輸入和輸出單元都只有 2個,即只能處理 2 個特徵的 2 分類問題, 首先使用 PCA 演算法 將特徵壓縮到 2 維, 輸出只判斷是不是第 1 類。格式如下:
| 輸入特徵1 | 輸入特徵2 | 輸出 |
|---|---|---|
| -2.684207 | 0.326607 | 0 |
| -2.715391 | -0.169557 | 0 |
| 1.464061 | 0.504190 | 1 |
此處不用在意 PCA 是怎麼回事, 將2維資料看做原始資料即可。
前向傳播
vec2mat($v, $r, $n)將向量 v 按行展開為 r x n 的矩陣(大多數實現都是按列展開);fill2d($r, $c, $v)生成一個大小為 r x c ,值全為 v 的矩陣;fp(array $a1, array $w)使用輸入矩陣 a1 和權重矩陣展開後的向量 w 計算輸出矩陣。
// ##### 前向傳播 ################
function fp(array $a1, array $w)
{
$m = count($a1);
$n = count($a1[0]);
$ws = array_chunk($w, 6);
$w1 = vec2mat($ws[0], 2, 3);
$w2 = vec2mat($ws[1], 2, 3);
$A1 = fill2d($m, 3, 1);
$a2 = fill2d($m, 2, 0);
$A2 = fill2d($m, 3, 1);
$a3 = fill2d($m, 2, 0);
// 輸入加偏執單元
for ($i = 0; $i < $m; $i++) {
$A1[$i][0] = 1;
$A1[$i][1] = $a1[$i][0];
$A1[$i][2] = $a1[$i][1];
}
// compute A2, a3
for ($i = 0; $i < $m; $i++) {
// 1 -> 2 層
// 加權和
$z11 = $A1[$i][0] * $w1[0][0] + $A1[$i][1] * $w1[0][1] + $A1[$i][2] * $w1[0][2];
$z12 = $A1[$i][0] * $w1[1][0] + $A1[$i][1] * $w1[1][1] + $A1[$i][2] * $w1[1][2];
$a2[$i][0] = sigmoid($z11);
$a2[$i][1] = sigmoid($z12);
// A2 加入偏置單元
$A2[$i][0] = 1;
$A2[$i][1] = $a2[$i][0];
$A2[$i][2] = $a2[$i][1];
// 2 -> 3 層
$z21 = $A2[$i][0] * $w2[0][0] + $A2[$i][1] * $w2[0][1] + $A2[$i][2] * $w2[0][2];
$z22 = $A2[$i][0] * $w2[1][0] + $A2[$i][1] * $w2[1][1] + $A2[$i][2] * $w2[1][2];
$a3[$i][0] = sigmoid($z21);
$a3[$i][1] = sigmoid($z22);
}
return $a3;
}計算損失
- a3 是最後一層的輸出
- y 是樣本輸出
- m 是樣本數量
- w 是引數矩陣
- lambda 是正則化引數
// 計算損失
$J = 0;
for ($i = 0; $i < $m; $i++) {
$J += pow($a3[$i][0] - $y[$i][0], 2) + pow($a3[$i][1] - $y[$i][1], 2);
}
$J = $J / (2 * $m);
// 加入正則化項
$r = 0;
for ($i = 0; $i < 2; $i++) {
// $j 從1開始也可以
for ($j = 0; $j < 3; $j++) {
$r += pow($w1[$i][$j], 2);
$r += pow($w2[$i][$j], 2);
}
}
$r = $r * $lambda / (2 * $m);
// 結構風險最小化損失
$Jsrm = $J + $r;反向傳播
- Ai 是第 i 層的輸出
mat2vec(array $m)將矩陣 m 按行展開為向量(大多數實現是按列)
// 初始化 J 對 w2 的偏導
$p2 = fill2d(2, 3, 0);
// 初始化 J 對 w1 的偏導
$p1 = fill2d(2, 3, 0);
for ($i = 0; $i < $m; $i++) {
$delta1 = 1 / $m * ($a3[$i][0] - $y[$i][0]) * $a3[$i][0] * (1 - $a3[$i][0]);
$delta2 = 1 / $m * ($a3[$i][1] - $y[$i][1]) * $a3[$i][1] * (1 - $a3[$i][1]);
$p2[0][0] += $delta1 * $A2[$i][0];
$p2[0][1] += $delta1 * $A2[$i][1];
$p2[0][2] += $delta1 * $A2[$i][2];
$p2[1][0] += $delta2 * $A2[$i][0];
$p2[1][1] += $delta2 * $A2[$i][1];
$p2[1][2] += $delta2 * $A2[$i][2];
}
// 加入正則化項的偏導
$p2[0][0] += $lambda / $m * $p2[0][0]; // 這一項不加也可以
$p2[0][1] += $lambda / $m * $p2[0][1];
$p2[0][2] += $lambda / $m * $p2[0][2];
$p2[1][0] += $lambda / $m * $p2[1][0]; // 這一項不加也可以
$p2[1][1] += $lambda / $m * $p2[1][1];
$p2[1][2] += $lambda / $m * $p2[1][2];
for ($i = 0; $i < $m; $i++) {
$delta1 = 1 / $m * (
($a3[$i][0] - $y[$i][0]) * $a3[$i][0] * (1 - $a3[$i][0]) * $w2[0][1] +
($a3[$i][1] - $y[$i][1]) * $a3[$i][1] * (1 - $a3[$i][1]) * $w2[1][1]
) * $A2[$i][1] * (1 - $A2[$i][1]);
$delta2 = 1 / $m * (
($a3[$i][0] - $y[$i][0]) * $a3[$i][0] * (1 - $a3[$i][0]) * $w2[0][2] +
($a3[$i][1] - $y[$i][1]) * $a3[$i][1] * (1 - $a3[$i][1]) * $w2[1][2]
) * $A2[$i][2] * (1 - $A2[$i][2]);
$p1[0][0] += $delta1 * $A1[$i][0];
$p1[0][1] += $delta1 * $A1[$i][1];
$p1[0][2] += $delta1 * $A1[$i][2];
$p1[1][0] += $delta2 * $A1[$i][0];
$p1[1][1] += $delta2 * $A1[$i][1];
$p1[1][2] += $delta2 * $A1[$i][2];
}
// 加入正則化項的偏導
$p1[0][0] += $lambda / $m * $p1[0][0]; // 這一項不加也可以
$p1[0][1] += $lambda / $m * $p1[0][1];
$p1[0][2] += $lambda / $m * $p1[0][2];
$p1[1][0] += $lambda / $m * $p1[1][0]; // 這一項不加也可以
$p1[1][1] += $lambda / $m * $p1[1][1];
$p1[1][2] += $lambda / $m * $p1[1][2];
// 偏導矩陣轉向量
$p = array_merge(mat2vec($p1), mat2vec($p2));梯度下降
- w 是各權重矩陣展開後組合而成的向量
- p 是各偏導矩陣展開後組合而成的向量
- alpha 是學習率
- 返回下降後的權重向量
// w <- w - alpha * (partial J) / (partial w)
function gradDesc(array $w, float $alpha, array $partial)
{
$n = count($w);
for ($i = 0; $i < $n; $i++) {
$w[$i] = $w[$i] - $alpha * $partial[$i];
}
return $w;
}訓練和測試
code/php/run.php 顯示了訓練和測試的過程
<?php
require("snn.php");
// 初始化迭代次數
$iter = 300;
// 初始化梯度下降引數
$alpha1 = array_pad([], $iter, 0.1); // 固定引數
$alpha2 = range($iter * 0.01, 0, -0.01); // 遞減引數
// 初始化正則化引數
$lambda = 1;
// 載入資料
$fx = file('iris-2.data');
$fy = file('iris-y.data');
$y = [];
$x = [];
$xTest = [];
$yTest = [];
// 取樣本資料
for ($i = 0; $i < 40; $i++) {
$x[] = str_getcsv($fx[$i]);
if (intval($fy[$i]) < 1) {
$y[] = [1, 0];
} else {
$y[] = [0, 1];
}
}
for ($i = 50; $i < 130; $i++) {
$x[] = str_getcsv($fx[$i]);
if (intval($fy[$i]) < 1) {
$y[] = [1, 0];
} else {
$y[] = [0, 1];
}
}
// 取測試資料
for ($i = 40; $i < 50; $i++) {
$xTest[] = str_getcsv($fx[$i]);
$yTest[] = intval($fy[$i]);
}
for ($i = 130; $i < 150; $i++) {
$xTest[] = str_getcsv($fx[$i]);
$yTest[] = intval($fy[$i]);
}
// 0 -> [1, 0], 1 -> [0, 1]
// 隨機初始化引數矩陣
$w1 = [];
$w2 = [];
for ($i = 0; $i < 2; $i++) {
$w1r = [];
$w2r = [];
for ($j = 0; $j < 3; $j++) {
$w1r[] = (rand(1, 99) - 50) / 100;
$w2r[] = (rand(1, 99) -50) / 100;
}
$w1[] = $w1r;
$w2[] = $w2r;
}
// 迭代
$JHistory = [];
$w = array_merge(mat2vec($w1), mat2vec($w2));
for ($i = 0; $i < $iter; $i++) {
$res = compute($x, $y, $w, $lambda);
$JHistory[] = $res["J"];
// 使用固定學習率
// $w = gradDesc($w, $alpha1[$i], $res["P"]);
// 使用遞減學習率
$w = gradDesc($w, $alpha2[$i], $res["P"]);
}
// 在測試集上驗證
$a3 = fp($xTest, $w);
$JHistory[] = $res["J"];
$hatY = [];
$total = 0;
$correct = 0;
$m = count($xTest);
for ($i = 0; $i < $m; $i++) {
$arr = $a3[$i];
// [0, 1]-> 1; [1, 0] -> 0
if ($arr[0] > $arr[1]) {
$hat = 0;
} else {
$hat = 1;
}
$hatY[] = $hat;
// 比較預測值和實際值
if ($hat <= intval($yTest[$i])) {
$correct++;
}
$total++;
}
// 輸出正確率
echo "Correct: $correct / $total\n";
// output: Correct: 30 / 30
// 儲存最終估計值
$csv = fopen("haty.csv", "w");
fputcsv($csv, $hatY);
fclose($csv);
// 儲存損失歷史
$csv = fopen("historyCost.csv", "w");
fputcsv($csv, $JHistory);
fclose($csv);
經過調節引數最終輸出正確穩定到 1。 以下為迭代誤差影像: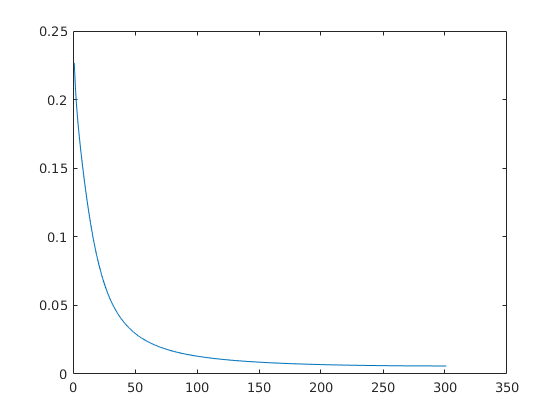
code/php/useApi.php 使用 fann 擴充套件對 4 特徵鳶尾花分類,
<?php
// 層數
$num_layers = 3;
// 第1層特徵數
$num_n1 = 4;
// 第2層特徵數
$num_n2 = 3;
// 第3層特徵數
$num_n3 = 3;
// 建立標準反向傳播神經網路
$fann = fann_create_standard($num_layers, $num_n1, $num_n2, $num_n3);
// 設定隱藏層啟用函式為 sigmoid
fann_set_activation_function_hidden($fann, FANN_SIGMOID);
// 設定輸出層啟用函式為 sigmoid
fann_set_activation_function_output($fann, FANN_SIGMOID);
// 設定訓練停止函式為 均方差
fann_set_train_stop_function($fann, FANN_STOPFUNC_MSE);
// 設定訓練演算法為每次求均方差後更新權重
fann_set_training_algorithm($fann, FANN_TRAIN_BATCH);
// 訓練次數
$iter = 1000;
// 使用者函式,無
$userFunc = 0;
// 誤差小於 $stopError 時停止訓練
$stopError = 1E-6;
// 由資料檔案進行訓練,
fann_train_on_file($fann, 'iris-4-train.data', $iter, $userFunc, $stopError);
// 儲存網路
fann_save($fann, 'fann.net');
// 讀測試資料
$x = fopen('iris-4-test-x.data', 'r');
// 執行測試
$hat = [];
while ($arr = fgetcsv($x)) {
$output = fann_run($fann, $arr);
arsort($output);
$hat[] = array_keys($output)[0];
}
fclose($x);
// 輸出預測值
echo join($hat, ","), PHP_EOL;
/*
* output:
* 0,0,0,0,0,0,0,0,0,0,1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2
*/
// 銷燬網路
fann_destroy($fann);
fann 使用的資料格式:
- 資料用空格和換行分割;
- 第 1 行 3 個數代表: "樣本數", "輸入特徵數", "輸出特徵數";
- 從第 2 行開始,依次為一行輸入, 一行輸出.
2 4 3
5.10 3.50 1.40 0.20
1 0 0
4.90 3.00 1.40 0.20
1 0 0梯度下降主要的問題在於,如果使用太大的學習率, 損失函式不能收斂,使用太小的學習率,函式將收斂到第一個遇到的區域性最小值。 區域性最小值會隨著神經元的增而增加。 對於這一問題, 本文采用的處理是, 學習率從大到小遞減(模擬退火)。 當隱藏層很多(深度學習網路),使用本文的方法幾乎不可能得到全域性最優解, 許多實現中用 遺傳演算法 求最佳化問題。
向量微分
由以下向量微分公式[6]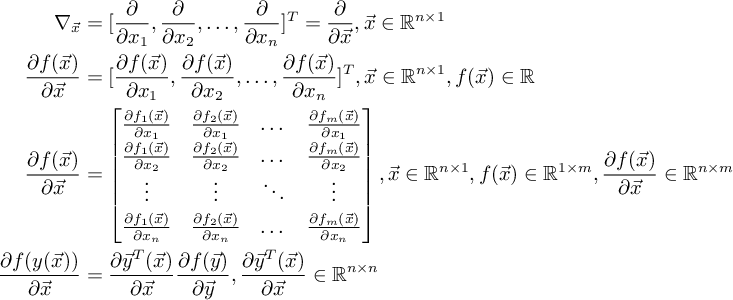
和 1.3式, 可以得出前向/反向傳播的一般情況。設:
那麼: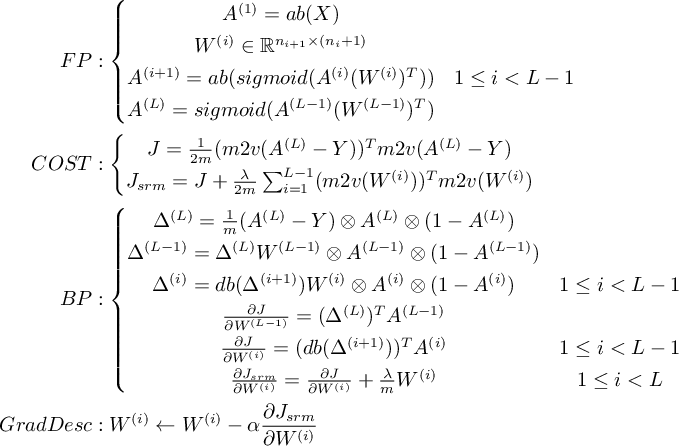
向量微分的性質可以直接推廣到矩陣。
矩陣 B = f(A),求 B 對 A 的導數 ∂B / ∂ A 即是 B 中每個元素分別對 A 中每個元素求導,可以分子 B 按行展開, 分母 A 按列展開, 或B按列展開,A按行展開,分別求導,使用哪一種展開規則都可以,只要保持一致(當使用不同的規則,有一種要轉置)即可。 然後將得到的微分單元按展開的規則逆向合併為一個矩陣,再由初等 行/列 變換化為最簡型。
Matlab/Octave 實現
[W, P] = initWeight(X, Y, hiddenLayer) 由輸入矩陣 X, 輸出矩陣 Y, 和隱藏層數目 hiddenLayer 初始化引數矩陣集合 W 和均方差對 W 的偏導矩陣集合 P
function [W, P] = initWeight(X, Y, hiddenLayer)
% 初始化引數和偏導矩陣%, 隱藏層單元數等於輸入層單元數, 全連線
% input:
% hidden_layer: scalar, number of hidden layer
% output:
% W: matrix cell array, weigth
% P: matrix cell array, partial
n1 = size(X, 2);
n2 = size(Y, 2);
for k = 1: hiddenLayer
W{k} = rand(n1, n1 + 1) - 0.5;
P{k} = zeros(n1, n1 + 1);
end
W{k + 1} = rand(n2, n1 + 1) - 0.5;
P{k + 1} = zeros(n1, n1 + 1);
endA = fp(X, W) 由輸入矩陣 X 和 引數矩陣集合 W 計算每層的輸出集合 A
function A = fp(X, W)
% 前向傳播
% input:
% X - matrix cell array
% W - matrix cell array
% output:
% A - matrix cell array
m = size(X, 1);
A{1} = [ones(m, 1), X];
for k = 1: length(W) - 1
A{k + 1} = [ones(m, 1), sigmoid(A{k} * (W{k})')];
end
A{k + 2} = sigmoid(A{k + 1} * (W{k + 1})');
endJ = cost(A, Y, W, lambda) 由輸出層輸出矩陣 X, 樣本輸出矩陣 Y, 引數矩陣集合 W, 正則化引數 lambda 計算正則化均方差 J
function J = cost(A, Y, W, lambda)
% 計算均方誤差
% input:
% A - matrix
% Y - matrix
% W - matrix cell array
% lambda - scalar
% output:
% J - scalar
m = size(Y, 1);
d = A - Y;
J = 1 / (2 * m) * d(:)' * d(:);
% 正則項
r = 0;
for k = 1: length(W)
w = W{k};
r = r + w(:)' * w(:);
end
r = lambda * r / (2 * m);
% 正則化誤差
J = J + r;
endP = bp(A, W, Y, lambda) 由每層輸出矩陣集合 A, 引數矩陣集合 W, 樣本輸出矩陣 Y, 正則化引數 lambda 計算均方差對 W 的偏導矩陣集合 P
function P = bp(A, W, Y, lambda)
% 後向傳播求偏導
% input:
% A - matrix cell array
% Y - matrix
% J - scalar
% output:
% P - matrix cell array
% 求每一層的偏導
m = size(Y, 1);
l = length(A);
Delta{l} = 1 / m * (A{l} - Y) .* (A{l} .* (1 - A{l}));
Delta{l - 1} = Delta{l} * W{l - 1} .* (A{l - 1} .* (1 - A{l - 1}));
for k = l - 2: -1: 2
% 偏置單元與前一層的偏導無關
D = Delta{k + 1}(:, 2: end);
Delta{k} = D * W{k} .* (A{k} .* (1 - A{k}));
end
% 求權重的偏導
l = length(W);
for k = 1: l - 1
D = Delta{k + 1}(:, 2: end);
P{k} = D' * A{k};
% 加入正則化項的偏導
P{k} = P{k} + lambda / m * W{k};
end
P{l} = (Delta{l + 1})' * A{l} + lambda / m * W{l};
endW = gradDesc(alpha, W, P) 由學習率 alpha, 引數矩陣集合 W, 均方差對 W 的偏導矩陣集合 P 計算梯度下降更新後的引數矩陣集合 W
function W = gradDesc(alpha, W, P)
% 梯度下降
% input:
% alpha - scalar, learning ratio
% W - matrix cell array, weight
% P - matrix cell array, partial
% output:
% W - matrix cell array, weight
for k = 1: length(W)
W{k} = W{k} - alpha * P{k};
end
endcode/matlab/run.m 使用以上函式測試鳶尾花分類
clear;close;clc;
% 準備資料
% matlab 可以使用 iris_dataset
% ##########################
% [X, Y] = iris_dataset;
% X = X';
% Y = Y';
% ##########################
% octave 需要手動下載資料
% ############################
data = load('iris-150x5.data');
X = data(:, 1:end-1);
y = data(:, end);
yu = unique(y);
yn = length(yu);
Y = zeros(length(y), yn);
for k = 1: yn
Y(:, k) = (y == yu(k));
end
% ############################
% 按列歸一化
for k = 1: size(X, 2)
X(:, k) = (X(:, k) - mean(X(:, k))) / (max(X(:, k)) - min(X(:, k)));
end
Xtrain = [X(1: 40, :); X(51: 90, :); X(101:140, :)];
Ytrain = [Y(1: 40, :); Y(51: 90, :); Y(101: 140, :)];
Xtest = [X(41: 50, :); X(91: 100, :); X(141: 150, :)];
Ytest = [Y(41: 50, :); Y(91: 100, :); Y(141: 150, :)];
% 建立一個神經網路
% 隱藏層數為: hidden_layer
% 連線方式為: 全連線
% 啟用單元為: sigmoid
% 隱藏層單元數為: 輸入層單元數
% 誤差為: 均方誤差
% 誤差傳遞方式: 反向傳播
% 最佳化演算法: 梯度下降
% 資料讀取方式: 每一行為一組資料
% 正則化項: l2
% 隱藏層
hiddenLayer = 2;
% 學習率, 其長度決定迭代次數
Alpha{1} = 10 * ones(500, 1);
Alpha{2} = 50: -0.1: 0.1;
% 正則化引數
lambda = 0.1;
% 訓練誤差
Jtrain = [];
% 測試誤差
Jtest = [];
[W, P] = initWeight(Xtrain, Ytrain, hiddenLayer);
A = fp(Xtrain, W);
color = '.rgbk';
for ia = 1: length(Alpha)
alpha = Alpha{ia};
iter = length(alpha);
for k = 1: iter
P = bp(A, W, Ytrain, lambda);
W = gradDesc(alpha(k), W, P);
A = fp(Xtrain, W);
Jtrain(k) = cost(A{hiddenLayer + 2}, Ytrain, W, lambda);
B = fp(Xtest, W);
Jtest(k) = cost(B{hiddenLayer + 2}, Ytest, W, lambda);
end
HatY = B{hiddenLayer + 2};
% 顯示結果, matlab 可以用 vec2ind
[value, index] = max(HatY');
disp(index);
plot(Jtrain, color(ia * 2)); hold on; plot(Jtest, color(ia * 2 + 1));
end
legend({'train(static)', 'test(static)', 'train(dynamic)', 'test(dynamic)'});
code/matlab/run.m 執行結果: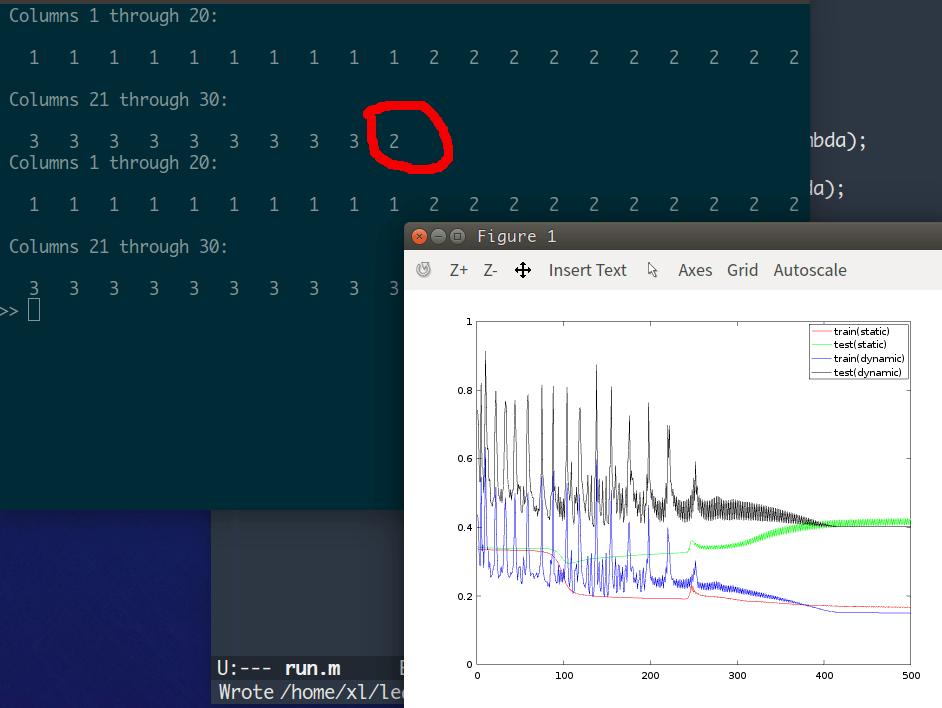
從上圖可以看出, 固定學習率為 10 的情況下,由於學習率稍大 (經測試 8 比較合適), 測試集的誤差 (綠線) 有小幅波動。 此時,即使對鳶尾花這個性質良好的資料分類,也有機率會出錯。
在這個例子中,初始學習率若小於 1, 函式也會收斂 (區域性最小值), 此時某一層的輸出會全為 0, 之後的輸出就沒有意義了, 對應輸出全為 1, 2, 3 中的一個。
硬體實現
圖3 所示網路只有加法單元, 乘法單元 和 s 單元,都是最基礎的數位電路原件,非常易於硬體實現, 用 FPGA 實現也非常容易。
神經網路的變化
從 圖3 可以看出,神經網路的變化在於神經元的啟用函式和連線方式, 比如:
- 當啟用函式使用卷積函式,構成卷積神經網路。
- 當連線中出現環路,構成遞迴神經網路,此時網路具有記憶,可以處理與順序有關的問題。
改變求最優解的方式不算改變神經網路。
過擬合
可以證明 , 隨著隱藏層的增加,神經網路可以以任意精度逼近任意連續函式。 神經網路的問題在於,對樣本的擬合能力太強,以至於不能很好的泛化到預測資料上。 matlab 中神經網路工具箱採用的做法是,將資料集隨機分出一部分作為測試集, 當訓練集和測試集的誤差都在減小則繼續迭代,若訓練集誤差下降而測試集誤差上升則 停止迭代。
另外,每次訓練隨機去掉一些神經元,也有助於削弱過擬合。
初始化權重的方式對神經網路有很大的影響。
更多內容參考[1]。
附件下載
下載地址 ,選擇附件: neuralNetwork.zip
檔案說明
- 如果環境為 Windows 或 OS X, 有可能資料檔案無法使用,執行
code/tools.py生成資料再複製到程式碼所在目錄即可 - 程式碼都是可以執行的,如果報錯,請檢查環境配置
code/matlab/SNN.m是一個物件導向的神經網路實現,需要稍作修改才能在 octave 中執行, 因為其中logsig和vec2ind函式是 matlab 才有的- 如果公式裡面的字看不清楚,可以檢視附件裡面的
nn.html,這個是 js 渲染的,可以無限放大 - 如果用 PHP 實現向量化運算, math-php, php-ml 是兩個現成的實現,但是它們的時間複雜度都是 O(n^3)。提供了一個用 php-cpp 封裝 arma 作為 PHP 擴充套件的例子:
linalgExtension, 時間複雜度大概是 O(n)。 對比了幾個 C 和 C++ 的庫,arma 基本是最好用的了
[1] 神經網路: MATLAB神經網路應用設計-第2版
[2] 最大似然估計: 機率論與數理統計,浙大第四版, ch7.1.2, p.152-153
[3] 鏈式法則: 高等數學(下), 同濟第七版, ch9.4, p.78-85
[4] 多元函式偏導數: 高等數學(下), 同濟第七版, ch9.2, p.65-71
[5] 梯度下降: 高等數學(下), 同濟第七版, ch9.7-9.8, p.103-111
[6] 向量微分: 矩陣分析與應用,清華第一版, ch5.1, p.255-271
本作品採用《CC 協議》,轉載必須註明作者和本文連結