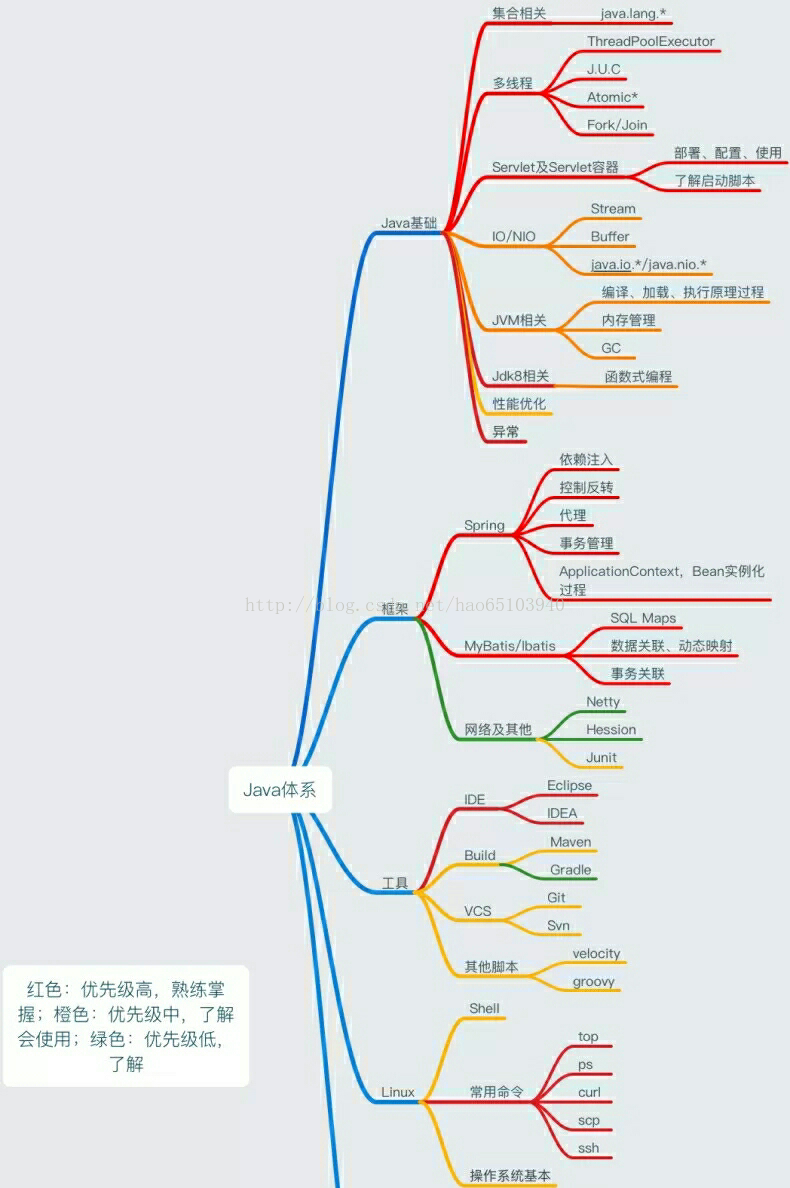
Java學習過程

個人分類： java

 

 

java詳細路線：

 

原文出自點選開啟連結

本文將告訴你學習Java需要達到的30個目標，學習過程中可能遇到的問題，及學習路線。希望能夠對你的學習有所幫助。對比一下自己，你已經掌握了這30條中的多少條了呢？

路線

Java發展到現在，按應用來分主要分為三大塊：J2SE,J2ME和J2EE。

這三塊相互補充，應用範圍不同。

J2SE就是Java2的標準版，主要用於桌面應用軟體的程式設計；

J2ME主要應用於嵌入是系統開發，如手機和PDA的程式設計；

J2EE是Java2的企業版，主要用於分散式的網路程式的開發，如電子商務網站和ERP系統。

先學習j2se

要學習j2ee就要先學習j2se，剛開始學習j2se先建議不要使用IDE，然後漸漸的過渡到使用IDE開發，畢竟用它方便嘛。學習j2se推薦兩本書，《java2核心技術一二卷》，《java程式設計思想》，《java模式》。其中《java程式設計思想》要研讀，精讀。這一段時間是基本功學習，時間會很長，也可能很短，這要看學習者自身水平而定。

不要被IDE糾纏

在學習java和j2ee過程中，你會遇到五花八門的IDE，不要被他們迷惑，學JAVA的時候，要學語言本身的東西，不要太在意IDE的附加功能，JAVA程式設計在不同IDE之間的轉換是很容易的，過於的在意IDE的功能反而容易耽誤對語言本身的理解。目前流行的IDE有jbuilder，eclipse和eclipse的加強版WSAD。用好其中一個就可以了，推薦從eclipse入手j2ee。因為Jbuilder更適合於寫j2se程式。

選擇和學習伺服器使用配置

當你有了j2se和IDE的經驗時，可以開始j2ee的學習了，web伺服器：tomcat，勿庸置疑，tomcat為學習web服務首選。而應用伺服器目前主要有三個：jboss、weblogic、websphere。有很多專案開始採用jboss，並且有大量的公司開始做websphere或weblogic向jboss應用伺服器的移植（節省成本），這裡要說的是，學習tomcat和jboss我認為是首選，也是最容易上手的。學習伺服器使用配置最好去詢問有經驗的人（有條件的話），因為他們或許一句話就能解決問題，你自己上網摸索可能要一兩天（我就幹過這種傻事），我們應該把主要時間放在學習原理和理論上，一項特定技術的使用永遠代替不了一個人的知識和學問。

學習web知識

如果你是在做電子商務網站等時，你可能要充當幾個角色，這是你還要學習：

html，可能要用到dreamwave等IDE。

Javascript，學會簡單的資料校驗，資料聯動顯示等等。

J2eeAPI學習

學習j2eeAPI和學習伺服器應該是一個迭代的過程。

先學習jsp和servlet程式設計，這方面的書很多，我建立看oreilly公司的兩本《jsp設計》和《java servlet程式設計》，oreilly出的書總是那本優秀，不得不佩服。

學習jdbc資料庫程式設計，j2ee專案大多都是MIS系統，訪問資料庫是核心。這本應屬於j2se學習中，這裡拿出來強調一下。

學習jndi api，它和學習ejb可以結合起來。

學習ejb api，推薦書《精通ejb》

經過上面的這些的學習，大概可以對付一般的應用了。

有人說跟著sun公司的《j2ee tutorial》一路學下來，當然也可以。

學習ejb設計模式和看程式碼（最重要）

設計模式是練內功，其重要性可以這麼說吧，如果你不會用設計模式的話，你將寫出一堆使用了ejb的垃圾，有慢又是一堆bug，其結果不如不用ejb實現（ejb不等於j2ee）

無論學習什麼語言，都應該看大量程式碼，你看的程式碼量不到一定數量，是學不好j2ee的。

目前有很多開源的工程可以作為教材：

jive論壇

petstore sun公司

dune sun公司

等等，研讀一個，並把它用到自己的工程中來。

J2ee其他學習

當你漸漸對j2ee瞭解到一定深度時，你要開始關注當前領域中的一些技術變化，J2ee是一塊百家爭鳴的領域，大家都在這裡提出自己的解決方案，例如structs，hiberate，ofbiz等等，學習這些東西要你的專案和目標而定，預先補充一下未嘗不可，但不用涉及太深，畢竟學習原理和理論是最最重要的事。

目前常見j2eeAPI

JavaServer Pages(JSP)技術1.2

Java Servlet技術2.3

JDBC API 2.0

Java XML處理API(JAXP)1.1

Enterprise JavaBeans技術2.0

Java訊息服務(JMS)1.0

Java命名目錄介面(JNDI)1.2

Java事務API(JTA) 1.0

JavaMail API 1.2

JavaBeans啟用架構(JAF)1.0

J2EE聯結器體系結構(JCA)1.0

Java認證和授權服務(JAAS)1.0

學習上面的某些API要以你的專案而定，瞭解所有他們總之是有好處的。

上面印證了大家說的一句話，java語言本身不難學，但是技術太多，所以學java很費勁。回想一下，基本上每個初學者，在剛學習java的時候可能都會問別人這麼一句話，你怎麼知道的哪個方法(api)在哪個包裡的？呵呵，無他，唯手熟爾。

1 基礎是王道。我們的基礎要紮實紮實再紮實。

以上面的整個流程來看java的技術分支很多，要想完全掌握是絕對不可能的。我們只有從中精通1到2個部分。但是java也是有通性的，所謂萬變不離其宗。java的所有程式設計思路都是“物件導向”的程式設計。所以大家在往更高境界發展以前一定要打好基礎，這樣不管以後是jree還是j3d都有應刃而解的感覺。在這裡強烈推薦“java程式設計思想”.

2 所謂打好基礎並不是說要熟悉所有的java程式碼。我說的意思是要了解java的結構。class,methode,object,各種套用import,extend 讓自己在結構上對java有個立體而且整體的瞭解即刻。其實java的學習不用固執於對程式碼的熟悉，1來java本身帶有很多demo，java2d

的所有問題幾乎都有demo的樣例。2來java是開放程式碼，即使沒有demo網路上也有很多高手把自己的程式碼分享。所以不要怕沒有參考，參考是到處都有的。

3 最後還有1點經驗和大家分享，對sun的api一定要學會活用，不論是學習還是作為參考api都有很大的幫助，在完全瞭解java的結構的基礎上，不論什麼方法都是可以通過api來找到的.所以不要怕找不到方法，瞭解結構，瞭解api就能找到方法。

重點

精通:能夠掌握此技術的85%技術要點以上，使用此技術時間超過兩年，並使用此技術成功實施5個以上的專案。能使用此技術優化效能或程式碼，做到最大可能的重用。

熟練：能夠掌握此技術的60%技術要點以上，使用此技術時間超過一年，並使用此技術成功實施3個以上的專案。能使用此技術實現軟體需求並有經驗的積累在實現之前能做優化設計儘可能的實現模組或程式碼的重用。

熟悉：能夠掌握此技術的50%技術要點以上，使用此技術時間超過半年上，並使用此技術成功實施1個以上的專案。能使用此技術實現軟體需求。

瞭解：可以在實際需要時參考技術文件或幫助檔案滿足你的需要，基本知道此項技術在你運用是所起的作用，能夠呼叫或者使用其根據規定提供給你的呼叫方式。

二：基本要求

1:html 掌握程度：熟練。原因：不會html你可能寫JSP?

2:javascript/jscript:掌握程度：熟悉。原因：client端的資料校驗、一些頁面處理需要你使用指令碼。

3:CSS 掌握程度：熟悉。原因：實現頁面風格的統一通常會使用css去實現。

4:java基礎程式設計 掌握程度：熟練。原因：不會java你能寫JSP?開玩笑吧。還有你必須非常熟悉以下幾個包java.lang;java.io;java.sql;java.util;java.text;javax.sevrlet;javax.servlet.http; javax.mail;等。

5:sql 掌握程度：熟練。原因：如果你不使用資料庫的話你也許不需要掌握sql。同時你必須對以下幾種資料庫中的一種以上的sql比較熟悉。Oracle,DB2,Mysql,Postgresql.

6:xml 掌握程度：瞭解 原因：AppServer的配置一般是使用XML來實現的。

7:ejb 掌握程度：瞭解 原因：很多專案中商業邏輯是由ejb來實現的，所以呢„„

8:以下幾種AppServer(engnier) 你需要了解一個以上。

a:)Tomcat b:)WebLogic c:)WebSphere d:)JRun e:)Resin 原因：你的jsp跑在什麼上面啊！

三：選擇要求(因專案而定)

1:LDAP 掌握程度：瞭解 原因：LADP越來越多的運用在許可權控制上面。

2:Struts 掌握程度：熟練 原因：如果符合MVC設計通常會使用Struts實現C。

3:Xsp 掌握程度：根據需要而定很多時候是不使用的，但在不需要使用ejb但jsp+servlet+bean實現不了的時候Xsp是一個非常不錯的選擇。

4:Linux 掌握程度：熟悉 原因：如果你的運用跑在Linux/Unix上你最少要知道rm ,mv,cp,vi,tar gzip/gunzip 是用來做什麼的吧。

四：工具的使用 1:UltraEdit(EditPlus)+jakarta-ant+jakarta-log4j; 2:Jubilder4-6 3:Visual Age For Java 4:VCafe

以上的工具你選擇你自己熟悉的吧。不過強烈建議你用log4j做除錯工具。

五：成長之路

1:html 學習時間，如果你的智商在80以上，15天時間應該夠用了。至少你能手寫出一個頁面來。

2:jacascript/jscript學習時間，這真的不好說，比較深奧的東西，夠用的話一個禮拜可以學寫皮毛。

3:css 學習時間,三天的時間你應該知道如何使用css了，不要求你寫，一般是美工來寫css。

4:java 學習時間，天才也的三個月吧。慢滿學吧。如果要精通，那我不知道需要多少時間了。用來寫

jsp,四個月應該夠了。

5:sql 學習時間，只需要知道insert ,delete ,update ,select,create/drop table的話一天你應該知道了。

6:xml 學習時間，我不知道我還沒有學會呢。呵呵。不過我知道DTD是用來做什麼的。

7:ejb 學習時間，基本的呼叫看3天你會呼叫了。不過是建立在你學會java的基礎上的。

8:熟悉AppServer,Tomcat四天你可以掌握安裝，配置。把jsp跑起來了。如果是WebLogic也夠了，但要使用ejb那不關你的事情吧。SA做什麼去了。

9:熟悉Linux那可得需要不少時間。慢慢看man吧。

10：Struts如果需要你再學習。

目標

1.你需要精通物件導向分析與設計(OOA/OOD)、涉及模式(GOF，J2EEDP)以及綜合模式。你應該十分了解UML，尤其是class，object，interaction以及statediagrams。

2. 你需要學習JAVA語言的基礎知識以及它的核心類庫(collections，serialization，streams， networking， multithreading，reflection，event，handling，NIO，localization，以及其他)。

3.你應該瞭解JVM，classloaders，classreflect，以及垃圾回收的基本工作機制等。你應該有能力反編譯一個類檔案並且明白一些基本的彙編指令。

4. 如果你將要寫客戶端程式，你需要學習WEB的小應用程式(applet)，必需掌握GUI設計的思想和方法，以及桌面程式的SWING，AWT， SWT。你還應該對UI部件的JAVABEAN元件模式有所瞭解。JAVABEANS也被應用在JSP中以把業務邏輯從表現層中分離出來。

5.你需要學習java資料庫技術，如JDBCAPI並且會使用至少一種persistence/ORM構架，例如Hibernate，JDO， CocoBase，TopLink，InsideLiberator(國產JDO紅工廠軟體)或者iBatis。

6.你還應該瞭解物件關係的阻抗失配的含義，以及它是如何影響業務物件的與關係型資料庫的互動，和它的執行結果，還需要掌握不同的資料庫產品運茫 熱?oracle，mysql，mssqlserver。

7.你需要學習JAVA的沙盒安全模式(classloaders，bytecodeverification，managers，policyandpermissions，

codesigning， digitalsignatures，cryptography，certification，Kerberos，以及其他)還有不同的安全/認證 API，例如JAAS(JavaAuthenticationandAuthorizationService)，JCE (JavaCryptographyExtension)，JSSE(JavaSecureSocketExtension)，以及JGSS (JavaGeneralSecurityService)。

8.你需要學習Servlets，JSP，以及JSTL(StandardTagLibraries)和可以選擇的第三方TagLibraries。

9.你需要熟悉主流的網頁框架，例如JSF，Struts，Tapestry，Cocoon，WebWork，以及他們下面的涉及模式，如MVC/MODEL2。

10.你需要學習如何使用及管理WEB伺服器，例如tomcat，resin，Jrun，並且知道如何在其基礎上擴充套件和維護WEB程式。

11.你需要學習分散式物件以及遠端API，例如RMI和RMI/IIOP。

12.你需要掌握各種流行中介軟體技術標準和與java結合實現，比如Tuxedo、CROBA，當然也包括javaEE本身。

13.你需要學習最少一種的XMLAPI，例如JAXP(JavaAPIforXMLProcessing)，JDOM(JavaforXMLDocumentObjectModel)，DOM4J，或JAXR(JavaAPIforXMLRegistries)。

14. 你應該學習如何利用JAVAAPI和工具來構建WebService。例如JAX-RPC(JavaAPIforXML/RPC)，SAAJ (SOAPwithAttachmentsAPIforJava)，JAXB(JavaArchitectureforXMLBinding)，JAXM (JavaAPIforXMLMessaging)， JAXR(JavaAPIforXMLRegistries)，或者JWSDP(JavaWebServicesDeveloperPack)。

15.你需要學習一門輕量級應用程式框架，例如Spring，PicoContainer，Avalon，以及它們的IoC/DI風格(setter，constructor，interfaceinjection)。

16. 你需要熟悉不同的J2EE技術，例如JNDI(JavaNamingandDirectoryInterface)，JMS (JavaMessageService)，JTA/JTS(JavaTransactionAPI/JavaTransactionService)， JMX (JavaManagementeXtensions)，以及JavaMail。

17.你需要學習企業級 JavaBeans(EJB)以及它們的不同元件模式：Stateless/StatefulSessionBeans，EntityBeans(包含 Bean- ManagedPersistence[BMP]或者Container-ManagedPersistence[CMP]和它的EJB-QL)，或者 Message-DrivenBeans(MDB)。

18.你需要學習如何管理與配置一個J2EE應用程式伺服器，如WebLogic，JBoss等，並且利用它的附加服務，例如簇類，連線池以及分散式處理支援。你還需要了解如何在它上面封裝和配置應用程式並且能夠監控、調整它的效能。

19.你需要熟悉面向方面的程式設計以及面向屬性的程式設計(這兩個都被很容易混淆的縮

寫為AOP)，以及他們的主流JAVA規格和執行。例如AspectJ和AspectWerkz。

20. 你需要熟悉對不同有用的API和frame work等來為你服務。例如Log4J(logging/tracing)，Quartz (scheduling)，JGroups(networkgroupcommunication)，JCache (distributedcaching)， Lucene(full-textsearch)，JakartaCommons等等。

21.如果你將要對接或者正和舊的系統或者本地平臺，你需要學習JNI (JavaNativeInterface) and JCA (JavaConnectorArchitecture)。

22.你需要熟悉JINI技術以及與它相關的分散式系統，比如掌握CROBA。

23.你需要JavaCommunityProcess(JCP)以及他的不同JavaSpecificationRequests(JSRs)，例如Portlets(168)，JOLAP(69)，DataMiningAPI(73)，等等。

24.你應該熟練掌握一種JAVAIDE例如sunOne，netBeans，IntelliJIDEA或者Eclipse。(有些人更喜歡VI或EMACS來編寫檔案。隨便你用什麼了：)

25.JAVA(精確的說是有些配置)是冗長的，它需要很多的人工程式碼(例如EJB)，所以你需要熟悉程式碼生成工具，例如XDoclet。

26.你需要熟悉一種單元測試體系(JNunit)，並且學習不同的生成、部署工具(Ant，Maven)。

27.你需要熟悉一些在JAVA開發中經常用到的軟體工程過程。例如RUP(RationalUnifiedProcess)andAgilemethodologies。

28.你需要能夠深入瞭解加熟練操作和配置不同的作業系統，比如GNU/linux，sunsolaris，macOS等，做為跨平臺軟體的開發者。

29.你還需要緊跟java發展的步伐，比如現在可以深入的學習javaME，以及各種java新規範，技術的運用，如新起的web富客戶端技術。

30.你必需要對opensource有所瞭解，因為至少java的很多技術直接是靠開源來驅動發展的，如java3D技術。(BlogJava-Topquan's Blog)

原文出自點選開啟連結

當然學習了基礎知識，也少不了瞭解一些資料結構與演算法

資料結構是以某種形式將資料組織在一起的集合，它不僅儲存資料，還支援訪問和處理資料的操作。演算法是為求解一個問題需要遵循的、被清楚指定的簡單指令的集合。下面是自己整理的常用資料結構與演算法相關內容，如有錯誤，歡迎指出。

為了便於描述，文中涉及到的程式碼部分都是用Java語言編寫的，其實Java本身對常見的幾種資料結構，線性表、棧、佇列等都提供了較好的實現，就是我們經常用到的Java集合框架，有需要的可以閱讀這篇文章。Java - 集合框架完全解析

1. 一、線性表

2. 1.陣列實現

3. 2.連結串列

4. 二、棧與佇列

5. 三、樹與二叉樹

6. 1.樹

7. 2.二叉樹基本概念

8. 3.二叉查詢樹

9. 4.平衡二叉樹

10. 5.紅黑樹

11. 四、圖

12. 五、總結

一、線性表

線性表是最常用且最簡單的一種資料結構，它是n個資料元素的有限序列。

實現線性表的方式一般有兩種，一種是使用陣列儲存線性表的元素，即用一組連續的儲存單元依次儲存線性表的資料元素。另一種是使用連結串列儲存線性表的元素，即用一組任意的儲存單元儲存線性表的資料元素（儲存單元可以是連續的，也可以是不連續的）。

陣列實現

陣列是一種大小固定的資料結構，對線性表的所有操作都可以通過陣列來實現。雖然陣列一旦建立之後，它的大小就無法改變了，但是當陣列不能再儲存線性表中的新元素時，我們可以建立一個新的大的陣列來替換當前陣列。這樣就可以使用陣列實現動態的資料結構。

• 程式碼1 建立一個更大的陣列來替換當前陣列

1. int[] oldArray = new int[10];

2.  

3. int[] newArray = new int[20];

4.  

5. for (int i = 0; i < oldArray.length; i++) {

6. newArray[i] = oldArray[i];

7. }

8.  

9. // 也可以使用System.arraycopy方法來實現陣列間的複製

10. // System.arraycopy(oldArray, 0, newArray, 0, oldArray.length);

11.  

12. oldArray = newArray;

• 程式碼2 在陣列位置index上新增元素e

1. //oldArray 表示當前儲存元素的陣列

2. //size 表示當前元素個數

3. public void add(int index, int e) {

4.  

5. if (index > size || index < 0) {

6. System.out.println("位置不合法...");

7. }

8.  

9. //如果陣列已經滿了 就擴容

10. if (size >= oldArray.length) {

11. // 擴容函式可參考程式碼1

12. }

13.  

14. for (int i = size - 1; i >= index; i--) {

15. oldArray[i + 1] = oldArray[i];

16. }

17.  

18. //將陣列elementData從位置index的所有元素往後移一位

19. // System.arraycopy(oldArray, index, oldArray, index + 1,size - index);

20.  

21. oldArray[index] = e;

22.  

23. size++;

24. }

上面簡單寫出了陣列實現線性表的兩個典型函式，具體我們可以參考Java裡面的ArrayList集合類的原始碼。陣列實現的線性表優點在於可以通過下標來訪問或者修改元素，比較高效，主要缺點在於插入和刪除的花費開銷較大，比如當在第一個位置前插入一個元素，那麼首先要把所有的元素往後移動一個位置。為了提高在任意位置新增或者刪除元素的效率，可以採用鏈式結構來實現線性表。

連結串列

連結串列是一種物理儲存單元上非連續、非順序的儲存結構，資料元素的邏輯順序是通過連結串列中的指標連結次序實現的。連結串列由一系列節點組成，這些節點不必在記憶體中相連。每個節點由資料部分Data和鏈部分Next，Next指向下一個節點，這樣當新增或者刪除時，只需要改變相關節點的Next的指向，效率很高。

單連結串列的結構

下面主要用程式碼來展示連結串列的一些基本操作，需要注意的是，這裡主要是以單連結串列為例，暫時不考慮雙連結串列和迴圈連結串列。

• 程式碼3 連結串列的節點

1. class Node<E> {

2.  

3. E item;

4. Node<E> next;

5.  

6. //建構函式

7. Node(E element) {

8. this.item = element;

9. this.next = null;

10. }

11. }

• 程式碼4 定義好節點後，使用前一般是對頭節點和尾節點進行初始化

1. //頭節點和尾節點都為空 連結串列為空

2. Node<E> head = null;

3. Node<E> tail = null;

• 程式碼5 空連結串列建立一個新節點

1. //建立一個新的節點 並讓head指向此節點

2. head = new Node("nodedata1");

3.  

4. //讓尾節點也指向此節點

5. tail = head;

• 程式碼6 連結串列追加一個節點

1. //建立新節點 同時和最後一個節點連線起來

2. tail.next = new Node("node1data2");

3.  

4. //尾節點指向新的節點

5. tail = tail.next;

• 程式碼7 順序遍歷連結串列

1. Node<String> current = head;

2. while (current != null) {

3. System.out.println(current.item);

4. current = current.next;

5. }

• 程式碼8 倒序遍歷連結串列

1. static void printListRev(Node<String> head) {

2. //倒序遍歷連結串列主要用了遞迴的思想

3. if (head != null) {

4. printListRev(head.next);

5. System.out.println(head.item);

6. }

7. }

• 程式碼 單連結串列反轉

1. //單連結串列反轉 主要是逐一改變兩個節點間的連結關係來完成

2. static Node<String> revList(Node<String> head) {

3.  

4. if (head == null) {

5. return null;

6. }

7.  

8. Node<String> nodeResult = null;

9.  

10. Node<String> nodePre = null;

11. Node<String> current = head;

12.  

13. while (current != null) {

14.  

15. Node<String> nodeNext = current.next;

16.  

17. if (nodeNext == null) {

18. nodeResult = current;

19. }

20.  

21. current.next = nodePre;

22. nodePre = current;

23. current = nodeNext;

24. }

25.  

26. return nodeResult;

27. }

上面的幾段程式碼主要展示了連結串列的幾個基本操作，還有很多像獲取指定元素，移除元素等操作大家可以自己完成，寫這些程式碼的時候一定要理清節點之間關係，這樣才不容易出錯。

連結串列的實現還有其它的方式，常見的有迴圈單連結串列，雙向連結串列，迴圈雙向連結串列。 迴圈單連結串列 主要是連結串列的最後一個節點指向第一個節點，整體構成一個鏈環。 雙向連結串列 主要是節點中包含兩個指標部分，一個指向前驅元，一個指向後繼元，JDK中LinkedList集合類的實現就是雙向連結串列。** 迴圈雙向連結串列** 是最後一個節點指向第一個節點。

二、棧與佇列

棧和佇列也是比較常見的資料結構，它們是比較特殊的線性表，因為對於棧來說，訪問、插入和刪除元素只能在棧頂進行，對於佇列來說，元素只能從佇列尾插入，從佇列頭訪問和刪除。

棧

棧是限制插入和刪除只能在一個位置上進行的表，該位置是表的末端，叫作棧頂，對棧的基本操作有push(進棧)和pop(出棧)，前者相當於插入，後者相當於刪除最後一個元素。棧有時又叫作LIFO(Last In First Out)表，即後進先出。

棧的模型

下面我們看一道經典題目，加深對棧的理解。

關於棧的一道經典題目

上圖中的答案是C，其中的原理可以好好想一想。

因為棧也是一個表，所以任何實現表的方法都能實現棧。我們開啟JDK中的類Stack的原始碼，可以看到它就是繼承類Vector的。當然，Stack是Java2前的容器類，現在我們可以使用LinkedList來進行棧的所有操作。

佇列

佇列是一種特殊的線性表，特殊之處在於它只允許在表的前端（front）進行刪除操作，而在表的後端（rear）進行插入操作，和棧一樣，佇列是一種操作受限制的線性表。進行插入操作的端稱為隊尾，進行刪除操作的端稱為隊頭。

佇列示意圖

我們可以使用連結串列來實現佇列，下面程式碼簡單展示了利用LinkedList來實現佇列類。

• 程式碼9 簡單實現佇列類

1. public class MyQueue<E> {

2.  

3. private LinkedList<E> list = new LinkedList<>();

4.  

5. // 入隊

6. public void enqueue(E e) {

7. list.addLast(e);

8. }

9.  

10. // 出隊

11. public E dequeue() {

12. return list.removeFirst();

13. }

14. }

普通的佇列是一種先進先出的資料結構，而優先佇列中，元素都被賦予優先順序。當訪問元素的時候，具有最高優先順序的元素最先被刪除。優先佇列在生活中的應用還是比較多的，比如醫院的急症室為病人賦予優先順序，具有最高優先順序的病人最先得到治療。在Java集合框架中，類PriorityQueue就是優先佇列的實現類，具體大家可以去閱讀原始碼。

三、樹與二叉樹

樹型結構是一類非常重要的非線性資料結構，其中以樹和二叉樹最為常用。在介紹二叉樹之前，我們先簡單瞭解一下樹的相關內容。

樹

** 樹 是由n（n>=1）個有限節點組成一個具有層次關係的集合。它具有以下特點：每個節點有零個或多個子節點；沒有父節點的節點稱為 根 節點；每一個非根節點有且只有一個 父節點 **；除了根節點外，每個子節點可以分為多個不相交的子樹。

樹的結構

二叉樹基本概念

• 定義

二叉樹是每個節點最多有兩棵子樹的樹結構。通常子樹被稱作“左子樹”和“右子樹”。二叉樹常被用於實現二叉查詢樹和二叉堆。

• 相關性質

二叉樹的每個結點至多隻有2棵子樹(不存在度大於2的結點)，二叉樹的子樹有左右之分，次序不能顛倒。

二叉樹的第i層至多有2(i-1)個結點；深度為k的二叉樹至多有2k-1個結點。

一棵深度為k，且有2^k-1個節點的二叉樹稱之為** 滿二叉樹 **；

深度為k，有n個節點的二叉樹，當且僅當其每一個節點都與深度為k的滿二叉樹中，序號為1至n的節點對應時，稱之為** 完全二叉樹 **。

• 三種遍歷方法

在二叉樹的一些應用中，常常要求在樹中查詢具有某種特徵的節點，或者對樹中全部節點進行某種處理，這就涉及到二叉樹的遍歷。二叉樹主要是由3個基本單元組成，根節點、左子樹和右子樹。如果限定先左後右，那麼根據這三個部分遍歷的順序不同，可以分為先序遍歷、中序遍歷和後續遍歷三種。

(1) 先序遍歷 若二叉樹為空，則空操作，否則先訪問根節點，再先序遍歷左子樹，最後先序遍歷右子樹。 (2) 中序遍歷 若二叉樹為空，則空操作，否則先中序遍歷左子樹，再訪問根節點，最後中序遍歷右子樹。(3) 後序遍歷 若二叉樹為空，則空操作，否則先後序遍歷左子樹訪問根節點，再後序遍歷右子樹，最後訪問根節點。

給定二叉樹寫出三種遍歷結果

• 樹和二叉樹的區別

(1) 二叉樹每個節點最多有2個子節點，樹則無限制。 (2) 二叉樹中節點的子樹分為左子樹和右子樹，即使某節點只有一棵子樹，也要指明該子樹是左子樹還是右子樹，即二叉樹是有序的。 (3) 樹決不能為空，它至少有一個節點，而一棵二叉樹可以是空的。

上面我們主要對二叉樹的相關概念進行了介紹，下面我們將從二叉查詢樹開始，介紹二叉樹的幾種常見型別，同時將之前的理論部分用程式碼實現出來。

二叉查詢樹

• 定義

二叉查詢樹就是二叉排序樹，也叫二叉搜尋樹。二叉查詢樹或者是一棵空樹，或者是具有下列性質的二叉樹： (1) 若左子樹不空，則左子樹上所有結點的值均小於它的根結點的值；(2) 若右子樹不空，則右子樹上所有結點的值均大於它的根結點的值；(3) 左、右子樹也分別為二叉排序樹；(4) 沒有鍵值相等的結點。

典型的二叉查詢樹的構建過程

• 效能分析

對於二叉查詢樹來說，當給定值相同但順序不同時，所構建的二叉查詢樹形態是不同的，下面看一個例子。

不同形態平衡二叉樹的ASL不同

可以看到，含有n個節點的二叉查詢樹的平均查詢長度和樹的形態有關。最壞情況下，當先後插入的關鍵字有序時，構成的二叉查詢樹蛻變為單支樹，樹的深度為n，其平均查詢長度(n+1)/2(和順序查詢相同），最好的情況是二叉查詢樹的形態和折半查詢的判定樹相同，其平均查詢長度和log2(n)成正比。平均情況下，二叉查詢樹的平均查詢長度和logn是等數量級的，所以為了獲得更好的效能，通常在二叉查詢樹的構建過程需要進行“平衡化處理”，之後我們將介紹平衡二叉樹和紅黑樹，這些均可以使查詢樹的高度為O(log(n))。

• 程式碼10 二叉樹的節點

1.  

2. class TreeNode<E> {

3.  

4. E element;

5. TreeNode<E> left;

6. TreeNode<E> right;

7.  

8. public TreeNode(E e) {

9. element = e;

10. }

11. }

二叉查詢樹的三種遍歷都可以直接用遞迴的方法來實現：

• 程式碼12 先序遍歷

1. protected void preorder(TreeNode<E> root) {

2.  

3. if (root == null)

4. return;

5.  

6. System.out.println(root.element + " ");

7.  

8. preorder(root.left);

9.  

10. preorder(root.right);

11. }

• 程式碼13 中序遍歷

1. protected void inorder(TreeNode<E> root) {

2.  

3. if (root == null)

4. return;

5.  

6. inorder(root.left);

7.  

8. System.out.println(root.element + " ");

9.  

10. inorder(root.right);

11. }

• 程式碼14 後序遍歷

1. protected void postorder(TreeNode<E> root) {

2.  

3. if (root == null)

4. return;

5.  

6. postorder(root.left);

7.  

8. postorder(root.right);

9.  

10. System.out.println(root.element + " ");

11. }

• 程式碼15 二叉查詢樹的簡單實現

1. /**

2. * @author JackalTsc

3. */

4. public class MyBinSearchTree<E extends Comparable<E>> {

5.  

6. // 根

7. private TreeNode<E> root;

8.  

9. // 預設建構函式

10. public MyBinSearchTree() {

11. }

12.  

13. // 二叉查詢樹的搜尋

14. public boolean search(E e) {

15.  

16. TreeNode<E> current = root;

17.  

18. while (current != null) {

19.  

20. if (e.compareTo(current.element) < 0) {

21. current = current.left;

22. } else if (e.compareTo(current.element) > 0) {

23. current = current.right;

24. } else {

25. return true;

26. }

27. }

28.  

29. return false;

30. }

31.  

32. // 二叉查詢樹的插入

33. public boolean insert(E e) {

34.  

35. // 如果之前是空二叉樹 插入的元素就作為根節點

36. if (root == null) {

37. root = createNewNode(e);

38. } else {

39. // 否則就從根節點開始遍歷 直到找到合適的父節點

40. TreeNode<E> parent = null;

41. TreeNode<E> current = root;

42. while (current != null) {

43. if (e.compareTo(current.element) < 0) {

44. parent = current;

45. current = current.left;

46. } else if (e.compareTo(current.element) > 0) {

47. parent = current;

48. current = current.right;

49. } else {

50. return false;

51. }

52. }

53. // 插入

54. if (e.compareTo(parent.element) < 0) {

55. parent.left = createNewNode(e);

56. } else {

57. parent.right = createNewNode(e);

58. }

59. }

60. return true;

61. }

62.  

63. // 建立新的節點

64. protected TreeNode<E> createNewNode(E e) {

65. return new TreeNode(e);

66. }

67.  

68. }

69.  

70. // 二叉樹的節點

71. class TreeNode<E extends Comparable<E>> {

72.  

73. E element;

74. TreeNode<E> left;

75. TreeNode<E> right;

76.  

77. public TreeNode(E e) {

78. element = e;

79. }

80. }

81.  

上面的程式碼15主要展示了一個自己實現的簡單的二叉查詢樹，其中包括了幾個常見的操作，當然更多的操作還是需要大家自己去完成。因為在二叉查詢樹中刪除節點的操作比較複雜，所以下面我詳細介紹一下這裡。

• 二叉查詢樹中刪除節點分析

要在二叉查詢樹中刪除一個元素，首先需要定位包含該元素的節點，以及它的父節點。假設current指向二叉查詢樹中包含該元素的節點，而parent指向current節點的父節點，current節點可能是parent節點的左孩子，也可能是右孩子。這裡需要考慮兩種情況：

1. current節點沒有左孩子，那麼只需要將patent節點和current節點的右孩子相連。
2. current節點有一個左孩子，假設rightMost指向包含current節點的左子樹中最大元素的節點，而parentOfRightMost指向rightMost節點的父節點。那麼先使用rightMost節點中的元素值替換current節點中的元素值，將parentOfRightMost節點和rightMost節點的左孩子相連，然後刪除rightMost節點。

1. // 二叉搜尋樹刪除節點

2. public boolean delete(E e) {

3.  

4. TreeNode<E> parent = null;

5. TreeNode<E> current = root;

6.  

7. // 找到要刪除的節點的位置

8. while (current != null) {

9. if (e.compareTo(current.element) < 0) {

10. parent = current;

11. current = current.left;

12. } else if (e.compareTo(current.element) > 0) {

13. parent = current;

14. current = current.right;

15. } else {

16. break;

17. }

18. }

19.  

20. // 沒找到要刪除的節點

21. if (current == null) {

22. return false;

23. }

24.  

25. // 考慮第一種情況

26. if (current.left == null) {

27. if (parent == null) {

28. root = current.right;

29. } else {

30. if (e.compareTo(parent.element) < 0) {

31. parent.left = current.right;

32. } else {

33. parent.right = current.right;

34. }

35. }

36. } else { // 考慮第二種情況

37. TreeNode<E> parentOfRightMost = current;

38. TreeNode<E> rightMost = current.left;

39. // 找到左子樹中最大的元素節點

40. while (rightMost.right != null) {

41. parentOfRightMost = rightMost;

42. rightMost = rightMost.right;

43. }

44.  

45. // 替換

46. current.element = rightMost.element;

47.  

48. // parentOfRightMost和rightMost左孩子相連

49. if (parentOfRightMost.right == rightMost) {

50. parentOfRightMost.right = rightMost.left;

51. } else {

52. parentOfRightMost.left = rightMost.left;

53. }

54. }

55.  

56. return true;

57. }

平衡二叉樹

平衡二叉樹又稱AVL樹，它或者是一棵空樹，或者是具有下列性質的二叉樹：它的左子樹和右子樹都是平衡二叉樹，且左子樹和右子樹的深度之差的絕對值不超過1。

平衡二叉樹

AVL樹是最先發明的自平衡二叉查詢樹演算法。在AVL中任何節點的兩個兒子子樹的高度最大差別為1，所以它也被稱為高度平衡樹，n個結點的AVL樹最大深度約1.44log2n。查詢、插入和刪除在平均和最壞情況下都是O（log n）。增加和刪除可能需要通過一次或多次樹旋轉來重新平衡這個樹。

紅黑樹

紅黑樹是平衡二叉樹的一種，它保證在最壞情況下基本動態集合操作的事件複雜度為O(log n)。紅黑樹和平衡二叉樹區別如下：(1) 紅黑樹放棄了追求完全平衡，追求大致平衡，在與平衡二叉樹的時間複雜度相差不大的情況下，保證每次插入最多隻需要三次旋轉就能達到平衡，實現起來也更為簡單。(2) 平衡二叉樹追求絕對平衡，條件比較苛刻，實現起來比較麻煩，每次插入新節點之後需要旋轉的次數不能預知。點選檢視更多

四、圖

• 簡介

圖是一種較線性表和樹更為複雜的資料結構，線上性表中，資料元素之間僅有線性關係，在樹形結構中，資料元素之間有著明顯的層次關係，而在圖形結構中，節點之間的關係可以是任意的，圖中任意兩個資料元素之間都可能相關。圖的應用相當廣泛，特別是近年來的迅速發展，已經滲入到諸如語言學、邏輯學、物理、化學、電訊工程、電腦科學以及數學的其他分支中。

• 相關閱讀

因為圖這部分的內容還是比較多的，這裡就不詳細介紹了，有需要的可以自己搜尋相關資料。

(1) 《百度百科對圖的介紹》
(2) 《資料結構之圖（儲存結構、遍歷）》

這篇文章是常見資料結構與演算法整理總結的下篇，上一篇主要是對常見的資料結構進行集中總結，這篇主要是總結一些常見的演算法相關內容，文章中如有錯誤，歡迎指出。

1. 一、概述

2. 二、查詢演算法

3. 三、排序演算法

4. 四、其它演算法

5. 五、常見演算法題

6. 六、總結

一、概述

以前看到這樣一句話，語言只是工具，演算法才是程式設計的靈魂。的確，演算法在電腦科學中的地位真的很重要，在很多大公司的筆試面試中，演算法掌握程度的考察都佔據了很大一部分。不管是為了面試還是自身程式設計能力的提升，花時間去研究常見的演算法還是很有必要的。下面是自己對於演算法這部分的學習總結。

演算法簡介

演算法是指解題方案的準確而完整的描述，是一系列解決問題的清晰指令，演算法代表著用系統的方法描述解決問題的策略機制。對於同一個問題的解決，可能會存在著不同的演算法，為了衡量一個演算法的優劣，提出了空間複雜度與時間複雜度這兩個概念。

時間複雜度

一般情況下，演算法中基本操作重複執行的次數是問題規模n的某個函式f(n)，演算法的時間度量記為 ** T(n) = O(f(n)) **，它表示隨問題規模n的增大，演算法執行時間的增長率和f(n)的增長率相同，稱作演算法的漸近時間複雜度，簡稱時間複雜度。這裡需要重點理解這個增長率。

1. 舉個例子，看下面3個程式碼：

2.  

3. 1、{++x;}

4.  

5. 2、for(i = 1; i <= n; i++) { ++x; }

6.  

7. 3、for(j = 1; j <= n; j++)

8. for(j = 1; j <= n; j++)

9. { ++x; }

10.  

11. 上述含有 ++x 操作的語句的頻度分別為1 、n 、n^2，

12.  

13. 假設問題的規模擴大了n倍，3個程式碼的增長率分別是1 、n 、n^2

14.  

15. 它們的時間複雜度分別為O(1)、O(n )、O(n^2)

16.  

空間複雜度

空間複雜度是對一個演算法在執行過程中臨時佔用儲存空間大小的量度，記做S(n)=O(f(n))。一個演算法的優劣主要從演算法的執行時間和所需要佔用的儲存空間兩個方面衡量。

二、查詢演算法

查詢和排序是最基礎也是最重要的兩類演算法，熟練地掌握這兩類演算法，並能對這些演算法的效能進行分析很重要，這兩類演算法中主要包括二分查詢、快速排序、歸併排序等等。

順序查詢

順序查詢又稱線性查詢。它的過程為：從查詢表的最後一個元素開始逐個與給定關鍵字比較，若某個記錄的關鍵字和給定值比較相等，則查詢成功，否則，若直至第一個記錄，其關鍵字和給定值比較都不等，則表明表中沒有所查記錄查詢不成功，它的缺點是效率低下。

二分查詢

• 簡介

二分查詢又稱折半查詢，對於有序表來說，它的優點是比較次數少，查詢速度快，平均效能好。

二分查詢的基本思想是將n個元素分成大致相等的兩部分，取a[n/2]與x做比較，如果x=a[n/2],則找到x，演算法中止；如果x<a[n/2]，則只要在陣列a的左半部分繼續搜尋x，如果x>a[n/2]，則只要在陣列a的右半部搜尋x。

二分查詢的時間複雜度為O(logn)

• 實現

1. //給定有序查詢表array 二分查詢給定的值data

2. //查詢成功返回下標 查詢失敗返回-1

3.  

4. static int funBinSearch(int[] array, int data) {

5.  

6. int low = 0;

7. int high = array.length - 1;

8.  

9. while (low <= high) {

10.  

11. int mid = (low + high) / 2;

12.  

13. if (data == array[mid]) {

14. return mid;

15. } else if (data < array[mid]) {

16. high = mid - 1;

17. } else {

18. low = mid + 1;

19. }

20. }

21. return -1;

22. }

三、排序演算法

排序是計算機程式設計中的一種重要操作，它的功能是將一個資料元素（或記錄）的任意序列，重新排列成一個按關鍵字有序的序列。下面主要對一些常見的排序演算法做介紹，並分析它們的時空複雜度。

常見排序演算法

常見排序演算法效能比較：

圖片來自網路

上面這張表中有穩定性這一項，排序的穩定性是指如果在排序的序列中，存在前後相同的兩個元素的話，排序前和排序後他們的相對位置不發生變化。

下面從氣泡排序開始逐一介紹。

氣泡排序

• 簡介

氣泡排序的基本思想是：設排序序列的記錄個數為n，進行n-1次遍歷，每次遍歷從開始位置依次往後比較前後相鄰元素，這樣較大的元素往後移，n-1次遍歷結束後，序列有序。

例如，對序列(3,2,1,5)進行排序的過程是：共進行3次遍歷，第1次遍歷時先比較3和2，交換，繼續比較3和1,交換，再比較3和5，不交換，這樣第1次遍歷結束，最大值5在最後的位置，得到序列(2,1,3,5)。第2次遍歷時先比較2和1，交換，繼續比較2和3，不交換，第2次遍歷結束時次大值3在倒數第2的位置，得到序列(1,2,3,5)，第3次遍歷時，先比較1和2，不交換，得到最終有序序列(1,2,3,5)。

需要注意的是，如果在某次遍歷中沒有發生交換，那麼就不必進行下次遍歷，因為序列已經有序。

• 實現

1. // 氣泡排序 注意 flag 的作用

2. static void funBubbleSort(int[] array) {

3.  

4. boolean flag = true;

5.  

6. for (int i = 0; i < array.length - 1 && flag; i++) {

7.  

8. flag = false;

9.  

10. for (int j = 0; j < array.length - 1 - i; j++) {

11.  

12. if (array[j] > array[j + 1]) {

13.  

14. int temp = array[j];

15. array[j] = array[j + 1];

16. array[j + 1] = temp;

17.  

18. flag = true;

19. }

20. }

21. }

22.  

23. for (int i = 0; i < array.length; i++) {

24. System.out.println(array[i]);

25. }

26. }

• 分析

最佳情況下氣泡排序只需一次遍歷就能確定陣列已經排好序，不需要進行下一次遍歷，所以最佳情況下，時間複雜度為** O(n) **。

最壞情況下氣泡排序需要n-1次遍歷，第一次遍歷需要比較n-1次，第二次遍歷需要n-2次，...，最後一次需要比較1次，最差情況下時間複雜度為** O(n^2) **。

簡單選擇排序

• 簡介

簡單選擇排序的思想是：設排序序列的記錄個數為n，進行n-1次選擇，每次在n-i+1(i = 1,2,...,n-1)個記錄中選擇關鍵字最小的記錄作為有效序列中的第i個記錄。

例如，排序序列(3,2,1,5)的過程是，進行3次選擇，第1次選擇在4個記錄中選擇最小的值為1，放在第1個位置，得到序列(1,3,2,5)，第2次選擇從位置1開始的3個元素中選擇最小的值2放在第2個位置，得到有序序列(1,2,3,5)，第3次選擇因為最小的值3已經在第3個位置不需要操作，最後得到有序序列（1,2,3,5）。

• 實現

1. static void funSelectionSort(int[] array) {

2.  

3. for (int i = 0; i < array.length - 1; i++) {

4.  

5. int mink = i;

6.  

7. // 每次從未排序陣列中找到最小值的座標

8. for (int j = i + 1; j < array.length; j++) {

9.  

10. if (array[j] < array[mink]) {

11. mink = j;

12. }

13. }

14.  

15. // 將最小值放在最前面

16. if (mink != i) {

17. int temp = array[mink];

18. array[mink] = array[i];

19. array[i] = temp;

20. }

21. }

22.  

23. for (int i = 0; i < array.length; i++) {

24. System.out.print(array[i] + " ");

25. }

26. }

• 分析

簡單選擇排序過程中需要進行的比較次數與初始狀態下待排序的記錄序列的排列情況** 無關。當i=1時，需進行n-1次比較；當i=2時，需進行n-2次比較；依次類推，共需要進行的比較次數是(n-1)+(n-2)+…+2+1=n(n-1)/2，即進行比較操作的時間複雜度為 O(n^2) ，進行移動操作的時間複雜度為 O(n) 。總的時間複雜度為 O(n^2) **。

最好情況下，即待排序記錄初始狀態就已經是正序排列了，則不需要移動記錄。最壞情況下，即待排序記錄初始狀態是按第一條記錄最大，之後的記錄從小到大順序排列，則需要移動記錄的次數最多為3（n-1）。

簡單選擇排序是不穩定排序。

直接插入排序

• 簡介

直接插入的思想是：是將一個記錄插入到已排好序的有序表中，從而得到一個新的、記錄數增1的有序表。

例如，排序序列(3,2,1,5)的過程是，初始時有序序列為(3)，然後從位置1開始，先訪問到2，將2插入到3前面，得到有序序列(2,3)，之後訪問1,找到合適的插入位置後得到有序序列(1,2,3)，最後訪問5，得到最終有序序列(1,2,3,5).

• 實現

1. static void funDInsertSort(int[] array) {

2.  

3. int j;

4.  

5. for (int i = 1; i < array.length; i++) {

6.  

7. int temp = array[i];

8.  

9. j = i - 1;

10.  

11. while (j > -1 && temp < array[j]) {

12.  

13. array[j + 1] = array[j];

14.  

15. j--;

16. }

17.  

18. array[j + 1] = temp;

19.  

20. }

21.  

22. for (int i = 0; i < array.length; i++) {

23. System.out.print(array[i] + " ");

24. }

25. }

• 分析

最好情況下，當待排序序列中記錄已經有序時，則需要n-1次比較，不需要移動，時間複雜度為** O(n) 。最差情況下，當待排序序列中所有記錄正好逆序時，則比較次數和移動次數都達到最大值，時間複雜度為 O(n^2) 。平均情況下，時間複雜度為 O(n^2) **。

希爾排序

希爾排序又稱“縮小增量排序”，它是基於直接插入排序的以下兩點性質而提出的一種改進：(1) 直接插入排序在對幾乎已經排好序的資料操作時，效率高，即可以達到線性排序的效率。(2) 直接插入排序一般來說是低效的，因為插入排序每次只能將資料移動一位。點選檢視更多關於希爾排序的內容

歸併排序

• 簡介

歸併排序是分治法的一個典型應用，它的主要思想是：將待排序序列分為兩部分，對每部分遞迴地應用歸併排序，在兩部分都排好序後進行合併。

例如，排序序列(3,2,8,6,7,9,1,5)的過程是，先將序列分為兩部分，(3,2,8,6)和(7,9,1,5)，然後對兩部分分別應用歸併排序，第1部分(3,2,8,6)，第2部分(7,9,1,5)，對兩個部分分別進行歸併排序，第1部分繼續分為(3,2)和(8,6)，(3,2)繼續分為(3)和(2)，(8,6)繼續分為(8)和(6)，之後進行合併得到(2,3)，(6,8)，再合併得到(2,3,6,8)，第2部分進行歸併排序得到(1,5,7,9)，最後合併兩部分得到(1,2,3,5,6,7,8,9)。

• 實現

1. //歸併排序

2. static void funMergeSort(int[] array) {

3.  

4. if (array.length > 1) {

5.  

6. int length1 = array.length / 2;

7. int[] array1 = new int[length1];

8. System.arraycopy(array, 0, array1, 0, length1);

9. funMergeSort(array1);

10.  

11. int length2 = array.length - length1;

12. int[] array2 = new int[length2];

13. System.arraycopy(array, length1, array2, 0, length2);

14. funMergeSort(array2);

15.  

16. int[] datas = merge(array1, array2);

17. System.arraycopy(datas, 0, array, 0, array.length);

18. }

19.  

20. }

21.  

22. //合併兩個陣列

23. static int[] merge(int[] list1, int[] list2) {

24.  

25. int[] list3 = new int[list1.length + list2.length];

26.  

27. int count1 = 0;

28. int count2 = 0;

29. int count3 = 0;

30.  

31. while (count1 < list1.length && count2 < list2.length) {

32.  

33. if (list1[count1] < list2[count2]) {

34. list3[count3++] = list1[count1++];

35. } else {

36. list3[count3++] = list2[count2++];

37. }

38. }

39.  

40. while (count1 < list1.length) {

41. list3[count3++] = list1[count1++];

42. }

43.  

44. while (count2 < list2.length) {

45. list3[count3++] = list2[count2++];

46. }

47.  

48. return list3;

49. }

• 分析

歸併排序的時間複雜度為O(nlogn)，它是一種穩定的排序，java.util.Arrays類中的sort方法就是使用歸併排序的變體來實現的。

快速排序

• 簡介

快速排序的主要思想是：在待排序的序列中選擇一個稱為主元的元素，將陣列分為兩部分，使得第一部分中的所有元素都小於或等於主元，而第二部分中的所有元素都大於主元，然後對兩部分遞迴地應用快速排序演算法。

• 實現

1. // 快速排序

2. static void funQuickSort(int[] mdata, int start, int end) {

3. if (end > start) {

4. int pivotIndex = quickSortPartition(mdata, start, end);

5. funQuickSort(mdata, start, pivotIndex - 1);

6. funQuickSort(mdata, pivotIndex + 1, end);

7. }

8. }

9.  

10. // 快速排序前的劃分

11. static int quickSortPartition(int[] list, int first, int last) {

12.  

13. int pivot = list[first];

14. int low = first + 1;

15. int high = last;

16.  

17. while (high > low) {

18.  

19. while (low <= high && list[low] <= pivot) {

20. low++;

21. }

22.  

23. while (low <= high && list[high] > pivot) {

24. high--;

25. }

26.  

27. if (high > low) {

28. int temp = list[high];

29. list[high] = list[low];

30. list[low] = temp;

31. }

32. }

33.  

34. while (high > first && list[high] >= pivot) {

35. high--;

36. }

37.  

38. if (pivot > list[high]) {

39. list[first] = list[high];

40. list[high] = pivot;

41. return high;

42. } else {

43. return first;

44. }

45. }

• 分析

在快速排序演算法中，比較關鍵的一個部分是主元的選擇。在最差情況下，劃分由n個元素構成的陣列需要進行n次比較和n次移動，因此劃分需要的時間是O(n)。在最差情況下，每次主元會將陣列劃分為一個大的子陣列和一個空陣列，這個大的子陣列的規模是在上次劃分的子陣列的規模上減1，這樣在最差情況下演算法需要(n-1)+(n-2)+...+1= ** O(n^2) **時間。

最佳情況下，每次主元將陣列劃分為規模大致相等的兩部分，時間複雜度為** O(nlogn) **。

堆排序

• 簡介

在介紹堆排序之前首先需要了解堆的定義，n個關鍵字序列K1，K2，…，Kn稱為堆，當且僅當該序列滿足如下性質（簡稱為堆性質）：(1) ki <= k(2i）且 ki <= k(2i+1) (1 ≤ i≤ n/2），當然，這是小根堆，大根堆則換成>=號。

如果將上面滿足堆性質的序列看成是一個完全二叉樹，則堆的含義表明，完全二叉樹中所有的非終端節點的值均不大於（或不小於）其左右孩子節點的值。

堆排序的主要思想是：給定一個待排序序列，首先經過一次調整，將序列構建成一個大頂堆，此時第一個元素是最大的元素，將其和序列的最後一個元素交換，然後對前n-1個元素調整為大頂堆，再將其第一個元素和末尾元素交換，這樣最後即可得到有序序列。

• 實現

1. //堆排序

2. public class TestHeapSort {

3.  

4. public static void main(String[] args) {

5. int arr[] = { 5, 6, 1, 0, 2, 9 };

6. heapsort(arr, 6);

7. System.out.println(Arrays.toString(arr));

8. }

9.  

10. static void heapsort(int arr[], int n) {

11.  

12. // 先建大頂堆

13. for (int i = n / 2 - 1; i >= 0; i--) {

14. heapAdjust(arr, i, n);

15. }

16.  

17. for (int i = 0; i < n - 1; i++) {

18. swap(arr, 0, n - i - 1);

19. heapAdjust(arr, 0, n - i - 1);

20. }

21. }

22.  

23. // 交換兩個數

24. static void swap(int arr[], int low, int high) {

25. int temp = arr[low];

26. arr[low] = arr[high];

27. arr[high] = temp;

28. }

29.  

30. // 調整堆

31. static void heapAdjust(int arr[], int index, int n) {

32.  

33. int temp = arr[index];

34.  

35. int child = 0;

36.  

37. while (index * 2 + 1 < n) {

38.  

39. child = index * 2 + 1;

40.  

41. // child為左右孩子中較大的那個

42. if (child != n - 1 && arr[child] < arr[child + 1]) {

43. child++;

44. }

45. // 如果指定節點大於較大的孩子 不需要調整

46. if (temp > arr[child]) {

47. break;

48. } else {

49. // 否則繼續往下判斷孩子的孩子 直到找到合適的位置

50. arr[index] = arr[child];

51. index = child;

52. }

53. }

54.  

55. arr[index] = temp;

56. }

57. }

58.  

• 分析

由於建初始堆所需的比較次數較多，所以堆排序不適宜於記錄數較少的檔案。堆排序時間複雜度也為O(nlogn)，空間複雜度為O(1)。它是不穩定的排序方法。與快排和歸併排序相比，堆排序在最差情況下的時間複雜度優於快排，空間效率高於歸併排序。

四、其它演算法

在上面的篇幅中，主要是對查詢和常見的幾種排序演算法作了介紹，這些內容都是基礎的但是必須掌握的內容，尤其是二分查詢、快排、堆排、歸併排序這幾個更是面試高頻考察點。（這裡不禁想起百度一面的時候讓我寫二分查詢和堆排序，二分查詢還行，然而堆排序當時一臉懵逼...）下面主要是介紹一些常見的其它演算法。

遞迴

• 簡介

在平常解決一些程式設計或者做一些演算法題的時候，經常會用到遞迴。程式呼叫自身的程式設計技巧稱為遞迴。它通常把一個大型複雜的問題層層轉化為一個與原問題相似的規模較小的問題來求解。上面介紹的快速排序和歸併排序都用到了遞迴的思想。

• 經典例子

斐波那契數列，又稱黃金分割數列、因數學家列昂納多·斐波那契以兔子繁殖為例子而引入，故又稱為“兔子數列”，指的是這樣一個數列：0、1、1、2、3、5、8、13、21、34、……在數學上，斐波納契數列以如下被以遞迴的方法定義：F（0）=0，F（1）=1，F（n）=F(n-1)+F(n-2)（n≥2，n∈N*）。

1. //斐波那契數列 遞迴實現

2. static long funFib(long index) {

3.  

4. if (index == 0) {

5. return 0;

6. } else if (index == 1) {

7. return 1;

8. } else {

9. return funFib(index - 1) + funFib(index - 2);

10. }

11. }

上面程式碼是斐波那契數列的遞迴實現，然而我們不難得到它的時間複雜度是O(2^n)，遞迴有時候可以很方便地解決一些問題，但是它也會帶來一些效率上的問題。下面的程式碼是求斐波那契數列的另一種方式，效率比遞迴方法的效率高。

1. static long funFib2(long index) {

2.  

3. long f0 = 0;

4. long f1 = 1;

5. long f2 = 1;

6.  

7. if (index == 0) {

8. return f0;

9. } else if (index == 1) {

10. return f1;

11. } else if (index == 2) {

12. return f2;

13. }

14.  

15. for (int i = 3; i <= index; i++) {

16. f0 = f1;

17. f1 = f2;

18. f2 = f0 + f1;

19. }

20.  

21. return f2;

22. }

分治演算法

分治演算法的思想是將待解決的問題分解為幾個規模較小但類似於原問題的子問題，遞迴地求解這些子問題，然後合併這些子問題的解來建立最終的解。分治演算法中關鍵地一步其實就是遞迴地求解子問題。關於分治演算法的一個典型例子就是上面介紹的歸併排序。檢視更多關於分治演算法的內容

動態規劃

動態規劃與分治方法相似，都是通過組合子問題的解來求解待解決的問題。但是，分治演算法將問題劃分為互不相交的子問題，遞迴地求解子問題，再將它們的解組合起來，而動態規劃應用於子問題重疊的情況，即不同的子問題具有公共的子子問題。動態規劃方法通常用來求解最優化問題。檢視更多關於動態規劃的內容

動態規劃典型的一個例子是最長公共子序列問題。

常見的演算法還有很多，比如貪心演算法，回溯演算法等等，這裡都不再詳細介紹，想要熟練掌握，還是要靠刷題，刷題，刷題，然後總結。

五、常見演算法題

下面是一些常見的演算法題彙總。

不使用臨時變數交換兩個數

1. static void funSwapTwo(int a, int b) {

2.  

3. a = a ^ b;

4. b = b ^ a;

5. a = a ^ b;

6.  

7. System.out.println(a + " " + b);

8. }

判斷一個數是否為素數

1. static boolean funIsPrime(int m) {

2.  

3. boolean flag = true;

4.  

5. if (m == 1) {

6. flag = false;

7. } else {

8.  

9. for (int i = 2; i <= Math.sqrt(m); i++) {

10. if (m % i == 0) {

11. flag = false;

12. break;

13. }

14. }

15. }

16.  

17. return flag;

18. }