攬貨最短路徑解決方案演算法 - C# 蟻群優化演算法實現

weixin_34037977發表於2018-02-25
演算法C#優化

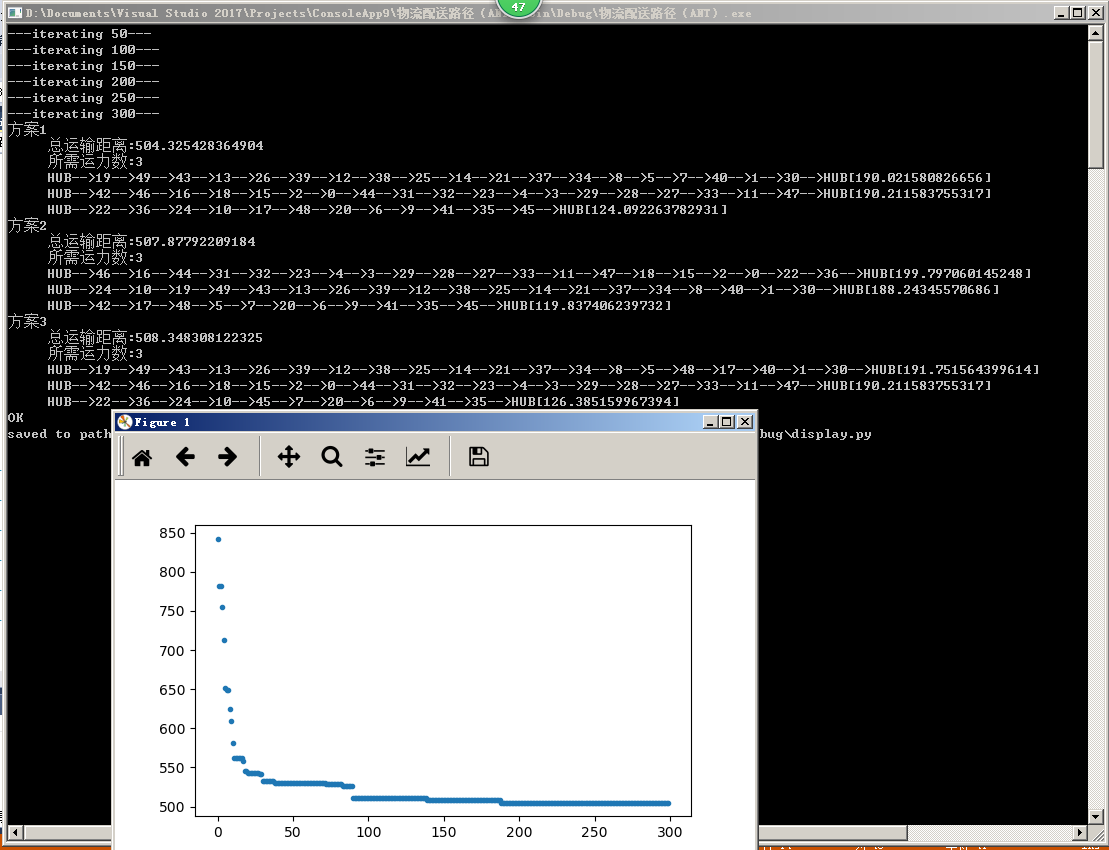
需求為（自己編的，非實際專案）：

某配送中心進行攬貨，目標客戶數為50個客戶，配送中心目前的運力資源如下：

  1. 現有車輛5臺
  2. 單臺運力最大行駛距離200千米
  3. 單臺運力最大載重公斤1噸

問：運力怎樣走法才能以最低的成本完成針對這50個客戶的攬貨行為

是個最優化問題（運籌學），我們只考慮簡化後的模型，不考慮路面交通、時間視窗這些複雜計算，用蟻群優化演算法來實現接近最優解的計算。

關於蟻群優化演算法的理論請看這篇文章：https://www.cnblogs.com/asxinyu/p/Path_Optimization_Tsp_Problem_Ant_System_CSharp.html

裡面的基本演算法已經寫明瞭，也有demo，本文是針對如何適應到具體業務的介紹（本文用的蟻群核心程式碼也是上文中改來的）

蟻群主要步驟為：

  1. 初始化（如資訊素）
  2. 開始迭代
    1. 構造各個螞蟻，以及螞蟻走的路徑（核心是針對後續節點的SELECT）
    2. 計算適應度
    3. 加入優秀螞蟻到跟蹤列表
    4. 更新資訊素（根據適應度）
  3. 結束迭代
  4. 給出報告

原文章裡用的是TSP做DEMO，比較難看清楚如何應用到實際業務邏輯中

同樣的，最困惑的核心中的核心，類似遺傳演算法，也是適應度值的計算，有的地方是一步一步增加vlaue，比如單純距離的增加，但是複雜點的都沒法這麼操作，而是要看整體路徑的指標（包括懲罰等）

由於蟻群優化演算法和本文程式碼都能下載，所以只介紹適應度value的計算

下載

 

class FitnessValueCalculator
    {
        private static int 擁有運力車輛數 = 5;
        private static int 單臺運力最大行駛距離 = 200;
        private static int 單臺運力最大載重公斤 = 1000;
        private static double 懲罰權重 = 20;

        public static double Calculator(ShortestDeliverAnt ant)
        {
            var paths = new List<string>();

            var distances = new List<double>();
            var weights = new List<double>();

            double 當前行駛距離 = 0;
            double 當前運力載重 = 0;
            string 當前行駛路徑 = "";
            int 當前所需運力數 = 1;

            //計算樞紐到第一個客戶配送距離
            當前行駛路徑 += "HUB-->" + ant.PathNodes.First();
            當前行駛距離 += ant.DistanceHelper.hub.DistanceTo(ant.DistanceHelper.customers[ant.PathNodes.First()]);
            當前運力載重 += ant.DistanceHelper.customers[ant.PathNodes.First()].需求量_公斤;

            foreach (var path in ant.Edges)
            {
                var fromNodeId = path.Key;
                var toNodeId = path.Value;

                var fromNode = ant.DistanceHelper.customers[fromNodeId];
                var toNode = ant.DistanceHelper.customers[toNodeId];

                double newAddedDistance2Customer = 0;
                double newAddedDistance2Hub = 0;
                double newAddedWeight = 0;

                newAddedDistance2Customer = fromNode.DistanceTo(toNode);
                newAddedDistance2Hub = toNode.DistanceTo(ant.DistanceHelper.hub);

                newAddedWeight = toNode.需求量_公斤;

                if (當前行駛距離 + newAddedDistance2Customer + newAddedDistance2Hub <= 單臺運力最大行駛距離
                    &&
                    當前運力載重 <= 單臺運力最大載重公斤)
                {
                    當前行駛距離 += newAddedDistance2Customer;
                    當前運力載重 += newAddedWeight;
                    當前行駛路徑 += "-->" + toNodeId;
                }
                else
                {
                    //加當前客戶距離、以及回到HUB的距離
                    當前行駛距離 += fromNode.DistanceTo(ant.DistanceHelper.hub);
                    distances.Add(當前行駛距離);

                    weights.Add(當前運力載重);

                    當前行駛路徑 += "-->HUB";
                    paths.Add(當前行駛路徑);

                    //RESET
                    當前行駛距離 = 0;
                    當前行駛距離 += ant.DistanceHelper.hub.DistanceTo(toNode);

                    當前運力載重 = 0;
                    當前運力載重 += toNode.需求量_公斤;

                    當前行駛路徑 = "";
                    當前行駛路徑 += "HUB-->" + toNodeId;

                    當前所需運力數++;
                }
            }

            //回到樞紐
            當前行駛距離 += ant.DistanceHelper.customers[ant.PathNodes.Last()].DistanceTo(ant.DistanceHelper.hub);
            distances.Add(當前行駛距離);

            當前行駛路徑 += "-->HUB";
            paths.Add(當前行駛路徑);



            int 懲罰係數 = 0;
            if (當前所需運力數 > 擁有運力車輛數)
                懲罰係數 = 當前所需運力數 - 擁有運力車輛數;


            ant.運輸距離順序 = distances;
            ant.運輸路徑 = paths;

            ant.Total行駛距離 = distances.Sum();
            ant.Total運力數 = 當前所需運力數;

            return ant.Total行駛距離 + 懲罰係數 * 懲罰權重;
        }
    }

 

ant.DistanceHelper.hub: 是配送中心的info，有地址資訊
ant.DistanceHelper.customers: 是50個客戶的info，也有地址資訊
目前為了簡化，是以街道距離來計算距離的
目前程式碼只是單目標優化演算法，非多目標優化，後續研究研究再發文。
上述程式碼其實就是第一輛車從配送中心開出到第一個客戶位置，然後加上客戶需求（攬的貨物重量）
接著判斷能否開到下一個客戶那裡攬貨，如果里程、重量都在限制條件只能，就開過去，不滿足條件就開回樞紐；然後繼續判斷第二輛車，也是這麼個邏輯
最終車輛的數量就是完成這50個客戶攬貨所需的運力數
萬一碰到所需運力超出了限制（程式碼中為5輛車），這時就需要懲罰，由於最終函式返回是double，而且是越小代表越優越，因此碰到了需要懲罰的情況，實際就是大幅度的增加返回值（適應度值）
紅色部分就是懲罰變數部分。

各種優化演算法的核心寫完框架後基本就不怎麼變化了，最易變的其實是適應度函式的計算，如果適應度計算中用到了預測技術，還得在上面那函式裡調機器學習的程式碼，感覺強化學習中動作施加後給出的反饋值也是這麼個值

程式碼下載

 

相關文章