權重隨機演算法的java實現

weixin_34037977發表於2017-06-30
隨機演算法Java

一、概述

　　平時，經常會遇到權重隨機演算法，從不同權重的N個元素中隨機選擇一個，並使得總體選擇結果是按照權重分佈的。如廣告投放、負載均衡等。

　　如有4個元素A、B、C、D，權重分別為1、2、3、4，隨機結果中A:B:C:D的比例要為1:2:3:4。

　　總體思路：累加每個元素的權重A(1)-B(3)-C(6)-D(10)，則4個元素的的權重管轄區間分別為[0,1)、[1,3)、[3,6)、[6,10)。然後隨機出一個[0,10)之間的隨機數。落在哪個區間，則該區間之後的元素即為按權重命中的元素。

　　實現方法：

利用TreeMap，則構造出的一個樹為:
　　　　B(3)
　　　 /      \
        /         \
     A(1)     D(10)
               /
             /
         C(6)

然後，利用treemap.tailMap().firstKey()即可找到目標元素。

當然，也可以利用陣列+二分查詢來實現。

二、原始碼

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
package com.xxx.utils;
 
import com.google.common.base.Preconditions;
import org.apache.commons.math3.util.Pair;
import org.slf4j.Logger;
import org.slf4j.LoggerFactory;
 
import java.util.List;
import java.util.SortedMap;
import java.util.TreeMap;
 
 
public class WeightRandom<K,V extends Number> {
    private TreeMap<Double, K> weightMap = new TreeMap<Double, K>();
    private static final Logger logger = LoggerFactory.getLogger(WeightRandom.class);
 
    public WeightRandom(List<Pair<K, V>> list) {
        Preconditions.checkNotNull(list, "list can NOT be null!");
        for (Pair<K, V> pair : list) {
            double lastWeight = this.weightMap.size() == 0 ? 0 : this.weightMap.lastKey().doubleValue();//統一轉為double
            this.weightMap.put(pair.getValue().doubleValue() + lastWeight, pair.getKey());//權重累加
        }
    }
 
    public K random() {
        double randomWeight = this.weightMap.lastKey() * Math.random();
        SortedMap<Double, K> tailMap = this.weightMap.tailMap(randomWeight, false);
        return this.weightMap.get(tailMap.firstKey());
    }
 
}

　　

　　

三、效能

4個元素A、B、C、D，其權重分別為1、2、3、4，執行1億次，結果如下：

元素 命中次數 誤差率
A 10004296 0.0430%
B 19991132 0.0443%
C 30000882 0.0029%
D 40003690 0.0092%

從結果，可以看出，準確率在99.95%以上。

 

四、另一種實現

利用B+樹的原理。葉子結點存放元素，非葉子結點用於索引。非葉子結點有兩個屬性，分別儲存左右子樹的累加權重。如下圖：

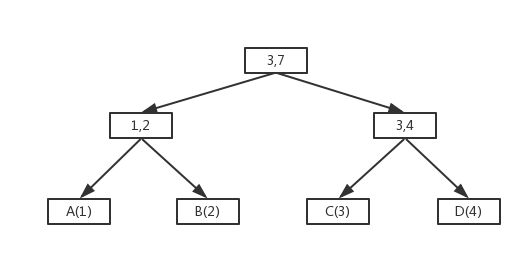
看到這個圖，聰明的你應該知道怎麼隨機了吧。

此方法的優點是：更改一個元素，只須修改該元素到根結點那半部分的權值即可。

end

相關文章