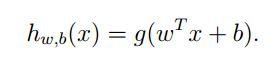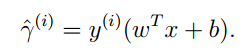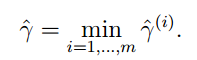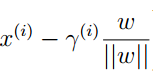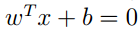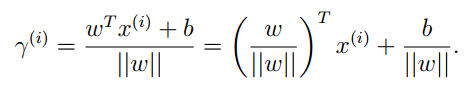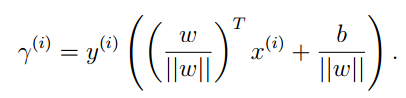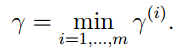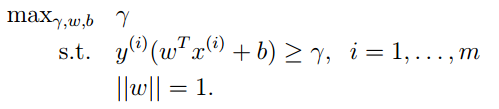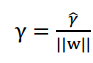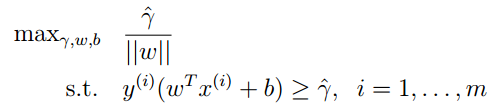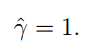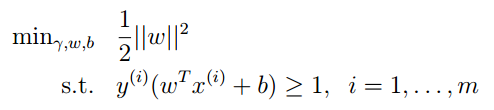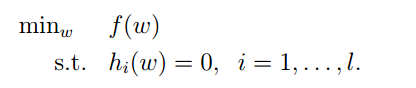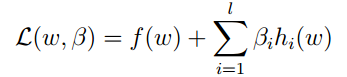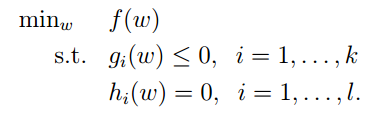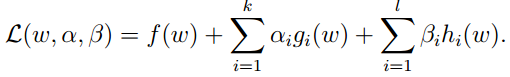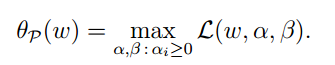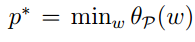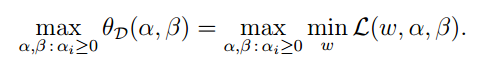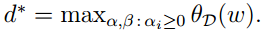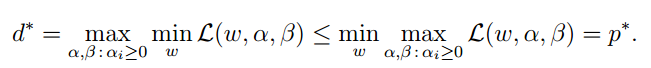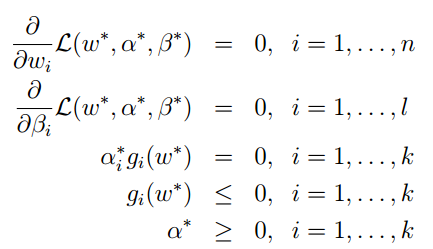這篇部落格主要解說了Ng的課第六、七個視訊,涉及到的內容包含,函式間隔和幾何間隔、最優間隔分類器 ( Optimal Margin
Classifier)、原始/對偶問題 ( Primal/Dual Problem)、 SVM 的對偶問題幾個部分。
- 函式間隔和幾何間隔
函式間隔( functional margin) 與幾何間隔( geometric margin)是理解SVM的基礎和前提。
如果y∈{-1,1},而不再是0,1,我們能夠將分類器函式表演示樣例如以下:
這裡的b引數事實上就是原來的X0,那麼我們能夠知道,W和B決定了一個確定的超平面。
給定一個訓練樣本,我們定義函式間隔:
則當y(i)=1的時候,為了使函式間隔最大,我們要使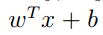
接下來我們能夠定義全域性的函式間隔:
也就是說全域性的函式間隔取決於函式間隔最小的那個樣本點。
但同一時候也不難發現這裡有一個問題,如果同一時候加大 w 和 b。則能夠非常easy的新增函式間隔。可是這樣對實際求解是沒有意義的的。我們為了限制 w 和 b。須要新增歸一化條件。
接下來引入幾何間隔:
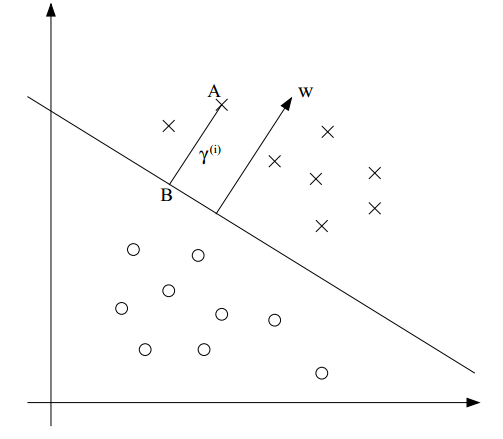
對於上面的圖片,如果切割面上有一點B,它是A在這個切割面上的投影。這個間隔我們用γ表示,那麼我們非常easy知道BA的方向事實上就是切割面的梯度方向。其單位向量是: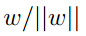
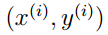
這樣我們不難表示出B點的座標:
將座標代入切割面方程
我們得到下式:
所以:
對於全域性的γ,我們須要乘上類別:
這就是點到平面的幾何間隔。我們不難看出,當||W||=1時。幾何間隔就是函式間隔。相同我們能夠定義全域性幾何間隔:
- 最優間隔分類器
我們的目標是尋找到一個超平面。使得這個平面與離它近期的點距離最大,而不關心其它的點到平面的距離。
形式化表演示樣例如以下:
接下來的目標就是求得這個切割面的引數W和b。可是我們看到上述函式的約束條件是||W||=1。這是一個球面,典型的非凸優化問題,難以求解。我們要進行適當的變換。考慮幾何間隔和函式間隔的關係:
我們能夠將原問題轉化為:
我們最好還是再令:
那麼原問題就是求取1/||W||的最大值。也就是||W||平方的最大值,原問題進一步能夠轉化為以下問題:
這個問題就變成了一個典型的二次規劃問題,原問題變得能夠求解。
- 拉格朗日對偶
為了求解上述問題。我們先看下一種最簡單的等式約束:
對於上述問題。我們一般能夠用拉格朗日乘子法來求解。引入變數β:
構造出上述拉格朗日乘式子。則原問題能夠通過分別對W和β求偏導數
並令偏導數為0來求解出W和β。詳細的數學證明就不在此解說了,本科《微積分》都學過。
以下我們就是要將等式的情況推廣到不等式,考慮到以下的求解問題:
存在不等式約束條件。依舊構造拉格朗日表示式:
由於兩個表示式。我們要引入αβ兩個變數。
依照之前的求解方法,這個問題求解會遇到一個非常大的問題:
由於g(W)<0,我們將α=正無窮,則表示式值變為負無窮,這樣是沒有意義的。因此我們必須避免這種情況,定義下式:
我們令α>0,則僅僅有 g 和 h 滿足約束時。 θ(w)為 f(w),也就是:
這樣原問題求 min f(w)就等價於求minθ(w)。
我們令:
又一次定義一個函式:
並令:
則有下列關係:
也就是最小值的最大值小於或等於最大值的最小值。這個問題是原問題的對偶問題。相對於原問題僅僅是更換了 min 和 max 的順序,在這裡取等號。條件例如以下描寫敘述:
①如果約束不等式 gi都是凸 ( convex)函式(線性函式都屬於凸函式)
②約束等式 hi 都是仿射( affine)函式(形如h(w)=wTx+b)
③而且存在 w使得對於全部的 i,gi(W)< 0
在這些如果下,肯定存在 ω∗, α∗, β∗,使得ω∗是原始問題的解, α∗, β∗是對偶問題的解,且P∗ = d∗ = L(ω∗, α∗, β∗)。這種ω∗, α∗, β∗須要滿足 KKT( Karush-Kuhn-Tucker)條件。 KKT條件例如以下:
如果ω∗, α∗, β∗滿足了庫恩-塔克條件,那麼他們就是原問題和對偶問題的解。
從上式能夠看出來:
α∗> 0,那麼gi(w∗) = 0。
滿足gi(w∗) = 0的w 處於可行域的邊界上。這時候的W才幹真正實用。內部的點,滿足gi(w∗) <0都是沒有意義的。這就引出了SVM的支援向量的概念。