圖論-BFS解無權有向圖最短路徑距離

weixin_33816946發表於2017-06-29

概述

本篇部落格主要內容：

對廣度優先搜尋演算法（Breadth-First-Search）進行介紹；
介紹用鄰接表的儲存結構實現一個圖（附C++實現原始碼）；
介紹用BFS演算法求解無權有向圖（附C++實現原始碼）。

廣度優先搜尋演算法（Breadth-First-Search）

廣度優先搜尋演算法（Breadth-First-Search）又被翻譯為寬度優先搜尋或橫向優先搜尋，簡稱BFS。

BFS是一種盲目搜尋法。其系統地展開並檢查圖中的所有頂點。BFS也是最簡便的圖搜尋演算法之中的一個，其相似思想被Dijkstra演算法和Prim演算法採用。
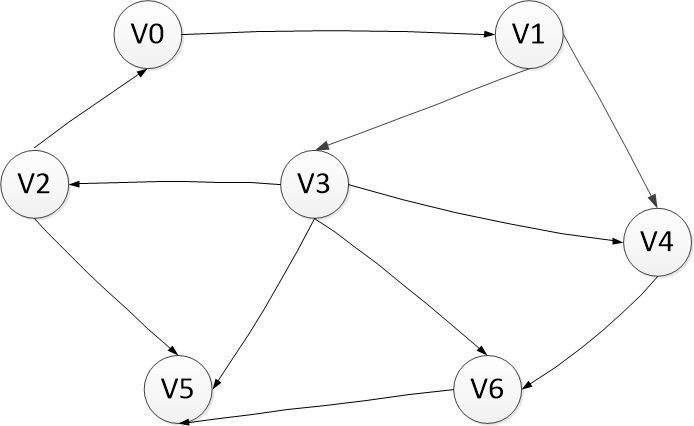
通過一個樣例來介紹BFS的思想，例如以下圖所看到的有一張由六個頂點組成的有向圖，當中圖中的每條邊的權值都是1（也能夠看做無權圖）。求解從一個頂點(源點)出發到圖中所有頂點的距離。

這裡寫圖片描寫敘述

選擇V2作為源點。尋找距離V2距離為2的頂點。找到V2;
尋找距離V2距離為1的頂點，找V2的出邊，找到V0和V5；
尋找距離V2距離為2的頂點。因為頂點V5的出度是0，所以找V0的出邊，找到V1;
尋找距離V2距離為3的頂點，找V1的出邊，找到V3和V4
尋找距離V2距離為4的頂點，找V3的出邊，找到V5和V6
於是圖中所有的頂點都被訪問過一次
總結一下搜尋的順序就是：V2–>V0–>V5–>V1–>V3–V4–>V5–>V6

這樣的搜尋圖的方法被稱為廣度優先搜尋（Breadth-First-Search）。該方法按層處理頂點。距離源點近期的那些頂點首先被求值，而最遠的那些頂點最後被求職。這非常像樹的層序遍歷（level-order-traversal）。

圖的鄰接表實現

用鄰接表實現一張圖。這裡採用的是兩個兩層連結串列的結構，當中一層連結串列儲存頂點資訊。每個頂點上有一個連結串列儲存該頂點的出邊。例如以下列虛擬碼所看到的：

#include <list>
class Edge {
    // ...
};

class VertexNode {
    std::list<Edge*> edgeAdj;    /* 頂點的鄰接表 */
    // ...
};
class Graph {
    // 頂點集合
    std::list<VertexNode*> vertexSet;
    //...

以下的程式碼給出邊的定義。
邊有三個屬性和三個方法：
- 屬性：權重、弧（有向邊）的起點和終點指標；
- 方法：獲取弧的起點、終點和權值

typedef class VertexNode _VertexNode;
// 邊的定義
class Edge {

    int weight;         /* 邊的權值 */
    _VertexNode * ori;  /* 弧的起點*/
    _VertexNode * des;  /* 弧的終點*/

public:

    Edge(int _weight,_VertexNode *_ori,_VertexNode *_des): weight(_weight),ori(_ori),des(_des){};
    ~Edge() {};

    // 獲取弧的起點
    _VertexNode* getOri() {return ori;};

    // 獲取弧的終點
    _VertexNode* getDes() {return des;};

    // 獲取弧的權值
    int getWeight() {return weight;};

};

以下程式碼給出了頂點的定義。頂點具有五個屬性和十個方法。

屬性的含義和方法的功能在程式碼的凝視中都有說明，這裡有兩點說明：

VISIT_STATUS狀態表示該頂點是否被訪問過。解決頂點反覆訪問的去重；
頂點定義key屬性，是頂點的標號。方便給大家演示。

typedef enum  _VISIT_STATUS{
    NO_VISIT,       /* 未訪問過此點 */
    VISIT_NO_ADJ,   /* 訪問過此點，但未訪問過其鄰接表 */
    VISIT_ADJ,      /* 訪問過此點和其鄰接表 */
} VISIT_STATUS;

class VertexNode {
    long key;               /* 頂點的關鍵字，用於標識該頂點*/
    int value;              /* 頂點附著的資訊 */
    std::list<Edge*> edgeAdj;/* 頂點的鄰接表 */
    VISIT_STATUS status;    /* 標識此頂點的訪問狀態 */
    int distence;           /* 此頂點與搜尋頂點的距離 */
    std::list<Edge*>::iterator iter_edge;/* 用於遍歷鄰接表 */
public:

    VertexNode(long _key,int _value) : key(_key), \
        value(_value) { distence = 0xFFFF;status = NO_VISIT; };
    ~VertexNode() {};

    // 獲取該頂點的關鍵字
    long getKey() { return key;};

    // 設定此頂點的關鍵字
    void setKey(long _key) { key = _key;};

    // 在頂點上加入一條弧
    void addEdge(Edge* _edge);

    // 在頂點上刪除一條弧
    void removeEdge(Edge* _edge);

    // 獲取鄰接表第一條邊
    Edge * getEdgeHeader() {
        iter_edge = edgeAdj.begin();
        return *iter_edge;
    };

    bool nextEdge(Edge **_edge) {
        iter_edge++;
        if (iter_edge != edgeAdj.end()) {
            *_edge = *iter_edge;
            return true;
        }
        return false;
    };

    // 獲取頂點的訪問狀態
    VISIT_STATUS getStatus() { return status;};

    // 設定頂點的訪問狀態
    void setStatus(VISIT_STATUS _status) {status = _status;};

    // 獲取出發點到此點的最小距離
    int getDistence() {return distence;};

    // 設定出發點到此點的最小距離
    void setDistence(int _distence) {distence = _distence;};

};

OKay，看過了邊和頂點的定義，以下程式碼給出圖的定義。主要有一個屬性vertexSet和三個方法組成。當中vertexSet屬性主要表示圖中頂點的集合。

typedef std::map<long, int>  DistenceOfGraph;

class Graph {
    // 頂點集合
    std::list<VertexNode*> vertexSet;

public:

    Graph() {};
    ~Graph() {};

    /* 功能找出key == _searchKey的頂點到圖中所有其他頂點的距離。注：不可達的頂點距離為0xFFFF
     * Input <long _searchKey> 查詢關鍵字
     * Output map<long, int>&dis 輸出結果。long 為關鍵字。int 為輸出結果
     */
    void bfs(long _searchKey,DistenceOfGraph &dis);

    // 列印圖中的所有頂點
    void printNode();

    // 列印頂點鍵值為key的邊
    void printEdge(long key);

    // 尋找頂點關鍵字為key的頂點，若找到由_node變數返回
    bool findNode(long key,VertexNode **_node);

    // 向圖中新增一個頂點
    VertexNode* addNode(long key,int value);

    // 向圖中新增一條邊
    void addEdge(long keyOri,long keyDes,int weight);

};

okay，如今我們已經完畢了圖的鄰接表儲存方式的定義，以上圖中的各方法將在後面詳細實現。

BFS演算法求解無權有向圖

在本文第一部分廣度優先搜尋那部分給出了一個求解無權有向圖的問題。以下我將結合此問題運用上面介紹的圖的鄰接表結構儲存來介紹BFS演算法的實現。

廣度優先搜尋過程中在訪問V1頂點鄰接表過程中，將V0和V5頂點後快取，然後處理V0,再將V0頂點鄰接表中的點快取起來。這個過程用到的快取結構事實上就是一個佇列。

在遍歷某一頂點的鄰接表的同一時候，將鄰接表中臨接的頂點快取到佇列中。依次處理。
還有就是一個去除反覆訪問的問題。為每個已經計算過距離的頂點。設定到達此點距離，並更新其狀態由未訪問過該頂點到訪問過該頂點但未訪問過其鄰接表。
OKay，說明了這兩點我們能夠一起看bfs方法的程式碼了。

// 通過輸入結點關鍵字_searchKey，找到該頂點
// 找到該頂點到圖中其他可達頂點的最小距離
void Graph::bfs(long _searchKey,DistenceOfGraph& dis) {
    queue<VertexNode*> queueCache;
    int distence = 0;
    // 若不存在此關鍵字，則返回
    VertexNode *node = NULL;
    if (!findNode(_searchKey, &node)) {
        return ;
    }

    // 查詢點距離查詢點的距離為0
    node->setDistence(0);
    node->setStatus(VISIT_NO_ADJ);
    (dis).insert(pair<long, int>(_searchKey,0));

    // 廣度優先遍歷圖
    while (IsNotNull(node)) {
        // 若頂點的鄰接表已經被訪問。則繼續訪問下一個頂點
        if ( JudgeNodeStatusVisitAdj(node) ) {
            // queue next
            QueueNext();
            continue;
        }

        // 遍歷頂點得所有臨界頂點
        Edge * edgeTmp = node->getEdgeHeader();
        while (IsNotNull(edgeTmp)) {
            // 獲取頂點的臨接點
            VertexNode * nodeTmp = edgeTmp->getDes();

            // 若該頂點未訪問過，則將此點加入佇列，並設定到此點的距離
            if (JudgeNodeStatusNoVisit(nodeTmp)) {
                queueCache.push(nodeTmp);
                distence = edgeTmp->getOri()->getDistence() + edgeTmp->getWeight();
                (dis).insert(pair<long, int>(GetDesNodeKey((edgeTmp)),distence));
                edgeTmp->getDes()->setDistence(distence);
                nodeTmp->setStatus(VISIT_NO_ADJ);

            }

            EdgeNext(edgeTmp);
        }

        QueueNext();
    }



    return;
}

相信到這裡，bfs演算法已經非常清晰了，那麼我在最後給出完整的實現程式碼和單元測試程式。

完整程式碼

標頭檔案：

#include <stdio.h>


#ifndef _GRAPH_BFS_H
#define _GRAPH_BFS_H

#include <list>
#include <map>

#define IsNotNull(a) (a)
#define IsNull(a) !(a)
#define JudgeNodeStatusVisitAdj(a) (a)->getStatus() == VISIT_ADJ
#define JudgeNodeStatusNoVisit(a) (a)->getStatus() == NO_VISIT
#define GetDistence(_edge) (_edge)->getOri()->getDistence() + (_edge)->getWeight()
#define GetOriNodeKey(_edge) (_edge)->getOri()->getKey()
#define GetDesNodeKey(_edge) (_edge)->getDes()->getKey()
#define EdgeNext(_edge) if (!node->nextEdge(&(_edge))) { break;}
#define QueueNext() if (queueCache.empty()) {break;} node = queueCache.front();queueCache.pop()
#define DistenceInsert(_dis,_edge) \
        DistenceOfGraph::iterator it = (_dis).find(GetOriNodeKey((_edge))); \
        if (it == (_dis).end() || GetDistence((_edge)) < it->second) { \
            cout<<"insert key = "<<GetOriNodeKey((_edge))<<"distence = "<<GetDistence((_edge))<<endl;\
            (_dis).insert(pair<long, int>(GetOriNodeKey((_edge)),GetDistence((_edge)))); \
        }


typedef class VertexNode _VertexNode;
typedef enum  _VISIT_STATUS{
    NO_VISIT,       /* 未訪問過此點 */
    VISIT_NO_ADJ,   /* 訪問過此點。但未訪問過其鄰接表 */
    VISIT_ADJ,      /* 訪問過此點和其鄰接表 */
} VISIT_STATUS;
typedef std::map<long, int>DistenceOfGraph;

// 邊
class Edge {

    int weight;         /* 邊的權值 */
    _VertexNode * ori;  /* 弧的起點*/
    _VertexNode * des;  /* 弧的終點*/

public:

    Edge(int _weight,_VertexNode *_ori,_VertexNode *_des): weight(_weight),ori(_ori),des(_des){};
    ~Edge() {};

    // 獲取弧的起點
    _VertexNode* getOri() {return ori;};

    // 獲取弧的終點
    _VertexNode* getDes() {return des;};

    // 獲取弧的權值
    int getWeight() {return weight;};

};

//頂點
class VertexNode {
    long key;               /* 頂點的關鍵字，用於標識該頂點*/
    int value;              /* 頂點附著的資訊 */
    std::list<Edge*> edgeAdj;    /* 頂點的鄰接表 */
    VISIT_STATUS status;    /* 標識此頂點的訪問狀態 */
    int distence;           /* 此頂點與搜尋頂點的距離 */
    std::list<Edge*>::iterator iter_edge;/* 用於遍歷鄰接表 */
public:

    VertexNode(long _key,int _value) : key(_key), \
        value(_value) { distence = 0xFFFF;status = NO_VISIT; };
    ~VertexNode() {};

    // 獲取該頂點的關鍵字
    long getKey() { return key;};

    // 設定此頂點的關鍵字
    void setKey(long _key) { key = _key;};

    // 在頂點上加入一條弧
    void addEdge(Edge* _edge);

    // 在頂點上刪除一條弧
    void removeEdge(Edge* _edge);

    // 獲取鄰接表第一條邊
    Edge * getEdgeHeader() {
        iter_edge = edgeAdj.begin();
        return *iter_edge;
    };

    bool nextEdge(Edge **_edge) {
        iter_edge++;
        if (iter_edge != edgeAdj.end()) {
            *_edge = *iter_edge;
            return true;
        }
        return false;
    };

    // 獲取頂點的訪問狀態
    VISIT_STATUS getStatus() { return status;};

    // 設定頂點的訪問狀態
    void setStatus(VISIT_STATUS _status) {status = _status;};

    // 獲取出發點到此點的最小距離
    int getDistence() {return distence;};

    // 設定出發點到此點的最小距離
    void setDistence(int _distence) {distence = _distence;};

};

class Graph {
    // 頂點集合
    std::list<VertexNode*> vertexSet;

public:

    Graph() {};
    ~Graph() {};

    /* 功能找出key == _searchKey的頂點到圖中所有其他頂點的距離。注：不可達的頂點距離為0xFFFF
     * Input <long _searchKey> 查詢關鍵字
     * Output map<long, int>&dis 輸出結果。long 為關鍵字。int 為輸出結果
     */
    void bfs(long _searchKey,DistenceOfGraph &dis);

    // 列印圖中的所有頂點
    void printNode();

    // 列印頂點鍵值為key的邊
    void printEdge(long key);

    // 尋找頂點關鍵字為key的頂點。若找到由_node變數返回
    bool findNode(long key,VertexNode **_node);

    // 向圖中新增一個頂點
    VertexNode* addNode(long key,int value);

    // 向圖中新增一條邊
    void addEdge(long keyOri,long keyDes,int weight);

};

// 此測試程式測試上面Graph中的bfs方法
int testGraphBfs();
#endif

程式碼實現的原始檔：

//
//  graph_bfs.cpp
//  100-alg-tests
//
//  Created by bobkentt on 15-8-8.
//  Copyright (c) 2015年 kedong. All rights reserved.
//
#include <iostream>
#include <queue>
#include <map>
#include <vector>
#include <list>
#include "graph_bfs.h"

using namespace std;

#define _DEBUG_ 1

void VertexNode::addEdge(Edge* _edge) {
    if (IsNull(_edge)) {
        cout<<"add an NULL edge."<<endl;
        exit(-1);
    }

#ifdef _DEBUG_
    cout<<"addEdge ori's key = "<<_edge->getOri()->getKey();
    cout<<",des's key ="<<_edge->getDes()->getKey()<<endl;;
#endif

    edgeAdj.push_back(_edge);

    return ;
}

bool Graph::findNode(long key,VertexNode **_node) {
    list<VertexNode*> &VS = vertexSet;
    list<VertexNode*>::iterator end = VS.end();
    list<VertexNode*>::iterator it;
    VertexNode *node = NULL;

    // 遍歷頂點集，找到開始結點A
    for (it = VS.begin(); it != end; it++) {
        node = *it;
        if (node->getKey() == key)
        {
            break;
        }
    }
    if (it == end) {
        // 結點中
        cout<<"graph::isNodeExist cannot find key = "<<key<<"in graph."<<endl;
        _node = NULL;
        return false;
    }
    *_node = node;
    return true;
}

VertexNode* Graph::addNode(long key,int value) {
    VertexNode * node = new VertexNode(key,value);

    vertexSet.push_back(node);

    return node;
}


void Graph::addEdge(long keyOri,long keyDes,int weight) {
    VertexNode *ori = NULL;
    VertexNode *des = NULL;

    // 在圖中查詢這兩個頂點
    if (!findNode(keyOri, &ori) || !findNode(keyDes, &des)) {
        cout<<"Graph::addEdge failed:未找到該頂點"<<endl;

        exit(-1);
    }

    // 建立此弧
    Edge * edge = new Edge(weight,ori,des);

    // 在圖中弧的起點的鄰接表中。加入此弧
    ori->addEdge(edge);

    return ;
}

// 通過輸入結點關鍵字_searchKey，找到該頂點
// 找到該頂點到圖中其他可達頂點的最小距離
void Graph::bfs(long _searchKey,DistenceOfGraph& dis) {
    queue<VertexNode*> queueCache;
    int distence = 0;
    // 若不存在此關鍵字，則返回
    VertexNode *node = NULL;
    if (!findNode(_searchKey, &node)) {
        return ;
    }

    // 查詢點距離查詢點的距離為0
    node->setDistence(0);
    node->setStatus(VISIT_NO_ADJ);
    (dis).insert(pair<long, int>(_searchKey,0));

    // 廣度優先遍歷圖
    while (IsNotNull(node)) {
        // 若頂點的鄰接表已經被訪問，則繼續訪問下一個頂點
        if ( JudgeNodeStatusVisitAdj(node) ) {
            // queue next
            QueueNext();
            continue;
        }

        // 遍歷頂點得所有臨界頂點
        Edge * edgeTmp = node->getEdgeHeader();
        while (IsNotNull(edgeTmp)) {
            // 獲取頂點的臨接點
            VertexNode * nodeTmp = edgeTmp->getDes();

            // 若該頂點未訪問過，則將此點加入佇列，並設定到此點的距離
            if (JudgeNodeStatusNoVisit(nodeTmp)) {
                queueCache.push(nodeTmp);
                distence = edgeTmp->getOri()->getDistence() + edgeTmp->getWeight();
                (dis).insert(pair<long, int>(GetDesNodeKey((edgeTmp)),distence));
                edgeTmp->getDes()->setDistence(distence);
                nodeTmp->setStatus(VISIT_NO_ADJ);

            }

            EdgeNext(edgeTmp);
        }

        QueueNext();
    }



    return;
}

void Graph::printNode() {
    list<VertexNode*>::iterator it = vertexSet.begin();
    cout<<"The nodes of Graph's keys = ";
    for (; it != vertexSet.end(); it++) {
        VertexNode * node = *it;
        cout<<node->getKey()<<" ";
    }
    cout<<endl;
    return ;
}

int testGraphBfs() {
    Graph G;

    // 畫出圖中所有的點
    for (int i = 0; i <= 6; i++) {
        G.addNode(i, i);
    }

    G.printNode();

    // 畫出圖中所有的邊
    G.addEdge(0, 1, 1);/* V0-->V1 */
    G.addEdge(0, 3, 1);/* V0-->V3 */
    G.addEdge(1, 3, 1);/* V1-->V3 */
    G.addEdge(1, 4, 1);/* V1-->V4 */
    G.addEdge(2, 0, 1);/* V2-->V0 */
    G.addEdge(2, 5, 1);/* V2-->V5 */
    G.addEdge(3, 2, 1);/* V3-->V2 */
    G.addEdge(3, 4, 1);/* V3-->V4 */
    G.addEdge(3, 5, 1);/* V3-->V5 */
    G.addEdge(3, 6, 1);/* V3-->V6 */
    G.addEdge(4, 6, 1);/* V4-->V6 */
    G.addEdge(6, 5, 1);/* V6-->V5 */

    // 選擇V3作為源點，求V3到其他所有的點的距離
    DistenceOfGraph dis;
    G.bfs(2, dis);

    // debug "for each dis"
    map<long,int>::iterator iter = dis.begin();
    for (; iter != dis.end(); iter++) {
        cout<<"key = "<<iter->first<<", dis = "<<iter->second<<endl;
    }


    return 0;
}

int main(int argc, const char * argv[]) {
    testGraphBfs();
    return 0;
}

Okay,今天就寫到這裡了。12點半了，困困噠。我要睡了，明天繼續，這周把DFS、Dijkstra、Prim演算法都實現一遍。
ps：這篇博文寫的匆忙，有哪些不好，或者不正確的地方請朋友們指正。

BFS求無權圖的單源最短路徑-鄰接矩陣儲存
2020-11-18
矩陣
圖論系列之「廣度優先遍歷及無權圖的最短路徑(ShortPath)」
2021-05-24
圖論
圖論-有向圖縮點
2018-04-22
圖論
Python 圖_系列之基於<連結表>實現無向圖最短路徑搜尋
2022-04-05
Python
圖論最短路總結
2020-07-03
圖論
DS圖—圖的最短路徑（不含程式碼框架）
2020-12-10
框架
圖論之有權圖「帶權圖的表示」
2021-05-25
圖論
圖的最短路徑演算法彙總
2020-11-30
演算法
演算法學習之路|有向無環圖（DAG）求最長路
2018-02-11
演算法
《圖論》——最短路徑 Dijkstra演算法(戴克斯特拉演算法)
2015-08-01
圖論演算法
最短路徑問題,BFS,408方向,思路與實現分析
2021-06-14
圖的單源最短路徑（Dijkstra演算法）
2017-12-19
演算法
SCU - 4444 別樣最短路徑-大資料完全圖
2015-10-01
大資料
圖論—尤拉回路/路徑
2024-03-24
圖論
用SQL解決有向圖問題
2009-03-06
SQL
《圖論》——廣度優先遍歷演算法(BFS)
2015-07-30
圖論演算法
圖 - 每對頂點間最短路徑----Floyd演算法
2013-09-02
演算法
二叉樹最大距離(直徑)
2017-05-17
二叉樹
用SQL解決有向圖問題(轉)
2019-03-23
SQL
圖論之有權圖「帶權圖的表示及相鄰節點迭代器」
2021-05-25
圖論
Python修改柱狀圖邊緣柱子與圖邊界的距離
2023-02-07
Python
演算法與資料結構之-圖的最短路徑
2019-03-04
演算法資料結構
資料結構學習（C++）——圖【4】（最短路徑） (轉)
2007-08-16
資料結構C++
JavaScript圖片橫向無縫滾動詳解
2018-09-07
JavaScript
計算地圖中兩點之間的距離
2022-01-17
地圖
傳說中的推土機距離基礎，最優傳輸理論瞭解一下
2018-10-04
最無恥的 HTTP 常用狀態碼圖解
2018-11-27
HTTP圖解
[簡易版]有向無環圖(DAG)前端視覺化
2018-11-25
前端視覺化
ggplot2中繪圖設定x軸、y軸名稱距離框線的距離
2024-03-08
繪圖
圖論之帶權圖「最小生成樹之Prim」
2021-05-26
圖論
UVA 10859 有向無環圖的動態規劃
2014-08-16
動態規劃
Python基於Excel資料加以反距離加權空間插值並掩膜圖層
2024-04-10
PythonExcel
win 10桌面圖示距離太大怎麼調小_win10桌面圖示間距突然變大如何恢復
2020-07-24
Win10
最優傳輸理論你理解了，傳說中的推土機距離重新瞭解一下
2018-10-10
有向圖的強連通性（java）
2019-01-25
Java
有向圖的拓撲排序——DFS
2022-12-30
排序
圖論之帶權圖「最小生成樹(Minimum Span Tree)」
2021-05-26
圖論
圖論之帶權圖「最小生成樹prim的優化」
2021-05-26
圖論優化

圖論-BFS解無權有向圖最短路徑距離

概述

廣度優先搜尋演算法（Breadth-First-Search）

圖的鄰接表實現

BFS演算法求解無權有向圖

完整程式碼

相關文章