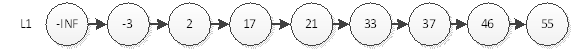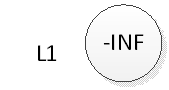【轉】跳躍表-原理及Java實現

原文地址：點選進入
引言：

上週現場面試阿里巴巴研發工程師終面，被問到如何讓連結串列的元素查詢接近線性時間。筆者苦思良久，繳械投降。面試官告知回去可以看一下跳躍表，遂出此文。

1、跳躍表的引入
我們知道，普通單連結串列查詢一個元素的時間複雜度為O(n)，即使該單連結串列是有序的，我們也不能通過2分的方式縮減時間複雜度。

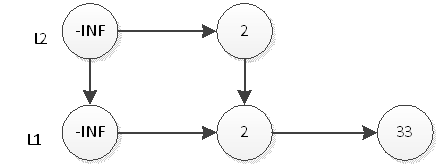
如上圖，我們要查詢元素為55的結點，必須從頭結點，迴圈遍歷到最後一個節點，不算-INF(負無窮)一共查詢8次。那麼用什麼辦法能夠用更少的次數訪問55呢？最直觀的，當然是新開闢一條捷徑去訪問55。

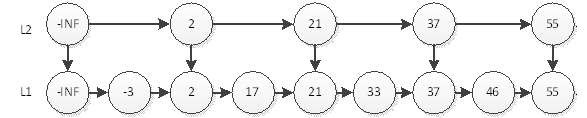
如上圖，我們要查詢元素為55的結點，只需要在L2層查詢4次即可。在這個結構中，查詢結點為46的元素將耗費最多的查詢次數5次。即先在L2查詢46，查詢4次後找到元素55，因為連結串列是有序的，46一定在55的左邊，所以L2層沒有元素46。然後我們退回到元素37，到它的下一層即L1層繼續搜尋46。非常幸運，我們只需要再查詢1次就能找到46。這樣一共耗費5次查詢。

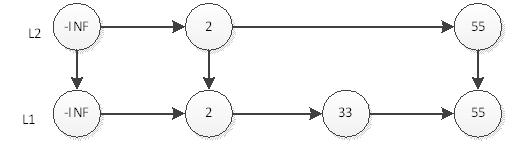
那麼，如何才能更快的搜尋55呢？有了上面的經驗，我們就很容易想到，再開闢一條捷徑。

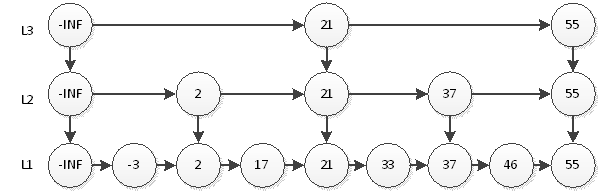
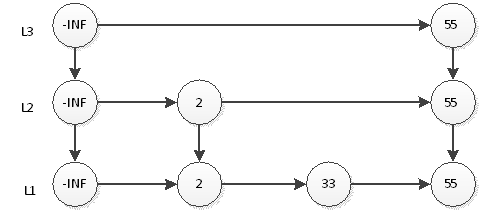
如上圖，我們搜尋55只需要2次查詢即可。這個結構中，查詢元素46仍然是最耗時的，需要查詢5次。即首先在L3層查詢2次，然後在L2層查詢2次，最後在L1層查詢1次，共5次。很顯然，這種思想和2分非常相似，那麼我們最後的結構圖就應該如下圖。

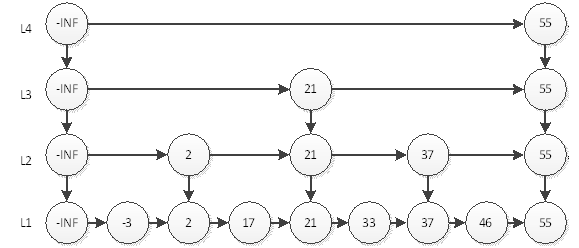
我們可以看到，最耗時的訪問46需要6次查詢。即L4訪問55，L3訪問21、55，L2訪問37、55，L1訪問46。我們直覺上認為，這樣的結構會讓查詢有序連結串列的某個元素更快。那麼究竟演算法複雜度是多少呢？

如果有n個元素，因為是2分，所以層數就應該是log n層 (本文所有log都是以2為底)，再加上自身的1層。以上圖為例，如果是4個元素，那麼分層為L3和L4，再加上本身的L2，一共3層；如果是8個元素，那麼就是3+1層。最耗時間的查詢自然是訪問所有層數，耗時logn+logn，即2logn。為什麼是2倍的logn呢？我們以上圖中的46為例，查詢到46要訪問所有的分層，每個分層都要訪問2個元素，中間元素和最後一個元素。所以時間複雜度為O(logn)。

至此為止，我們引入了最理想的跳躍表，但是如果想要在上圖中插入或者刪除一個元素呢？比如我們要插入一個元素22、23、24……，自然在L1層，我們將這些元素插入在元素21後，那麼L2層，L3層呢？我們是不是要考慮插入後怎樣調整連線，才能維持這個理想的跳躍表結構。我們知道，平衡二叉樹的調整是一件令人頭痛的事情，左旋右旋左右旋……一般人還真記不住，而調整一個理想的跳躍表將是一個比調整平衡二叉樹還複雜的操作。幸運的是，我們並不需要通過複雜的操作調整連線來維護這樣完美的跳躍表。有一種基於概率統計的插入演算法，也能得到時間複雜度為O(logn)的查詢效率，這種跳躍表才是我們真正要實現的。

2、容易實現的跳躍表
容易實現的跳躍表，它允許簡單的插入和刪除元素，並提供O(logn)的查詢時間複雜度，以下我們簡稱為跳躍表。

先討論插入，我們先看理想的跳躍表結構，L2層的元素個數是L1層元素個數的1/2，L3層的元素個數是L2層的元素個數的1/2，以此類推。從這裡，我們可以想到，只要在插入時儘量保證上一層的元素個數是下一層元素的1/2，我們的跳躍表就能成為理想的跳躍表。那麼怎麼樣才能在插入時保證上一層元素個數是下一層元素個數的1/2呢？很簡單，拋硬幣就能解決了！假設元素X要插入跳躍表，很顯然，L1層肯定要插入X。那麼L2層要不要插入X呢？我們希望上層元素個數是下層元素個數的1/2，所以我們有1/2的概率希望X插入L2層，那麼拋一下硬幣吧，正面就插入，反面就不插入。那麼L3到底要不要插入X呢？相對於L2層，我們還是希望1/2的概率插入，那麼繼續拋硬幣吧！以此類推，元素X插入第n層的概率是(1/2)的n次。這樣，我們能在跳躍表中插入一個元素了。

在此還是以上圖為例：跳躍表的初試狀態如下圖，表中沒有一個元素：

如果我們要插入元素2，首先是在底部插入元素2，如下圖：

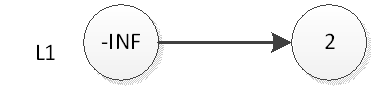
然後我們拋硬幣，結果是正面，那麼我們要將2插入到L2層，如下圖

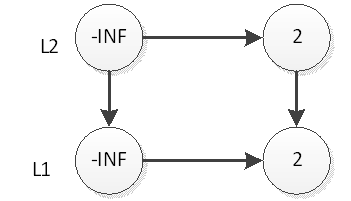
繼續拋硬幣，結果是反面，那麼元素2的插入操作就停止了，插入後的表結構就是上圖所示。接下來，我們插入元素33，跟元素2的插入一樣，現在L1層插入33，如下圖：

然後拋硬幣，結果是反面，那麼元素33的插入操作就結束了，插入後的表結構就是上圖所示。接下來，我們插入元素55，首先在L1插入55，插入後如下圖：

繼續拋硬幣，結果又是正面，那麼L3層需要插入55，如下圖：

繼續拋硬幣，結果又是正面，那麼要在L4插入55，結果如下圖：

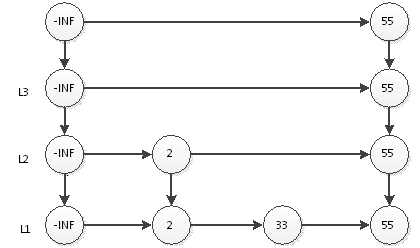
繼續拋硬幣，結果是反面，那麼55的插入結束，表結構就如上圖所示。

以此類推，我們插入剩餘的元素。當然因為規模小，結果很可能不是一個理想的跳躍表。但是如果元素個數n的規模很大，學過概率論的同學都知道，最終的表結構肯定非常接近於理想跳躍表。

當然，這樣的分析在感性上是很直接的，但是時間複雜度的證明實在複雜，在此我就不深究了，感興趣的可以去看關於跳躍表的paper。

再討論刪除，刪除操作沒什麼講的，直接刪除元素，然後調整一下刪除元素後的指標即可。跟普通的連結串列刪除操作完全一樣。

再來討論一下時間複雜度，插入和刪除的時間複雜度就是查詢元素插入位置的時間複雜度，這不難理解，所以是O(logn)。

3、JAVA實現
在章節2中，我們採用拋硬幣的方式來決定新元素插入的最高層數，這當然不能在程式中實現。程式碼中，我們採用隨機數生成的方式來獲取新元素插入的最高層數。我們先估摸一下n的規模，然後定義跳躍表的最大層數maxLevel，那麼底層，也就是第0層，元素是一定要插入的，概率為1；最高層，也就是maxLevel層，元素插入的概率為1/2^maxLevel。

我們先隨機生成一個範圍為0~2^maxLevel-1的一個整數r。那麼元素r小於2^(maxLevel-1)的概率為1/2，r小於2^(maxLevel-2)的概率為1/4，……，r小於2的概率為1/2^(maxLevel-1)，r小於1的概率為1/2^maxLevel。

舉例，假設maxLevel為4，那麼r的範圍為0~15，則r小於8的概率為1/2，r小於4的概率為1/4，r小於2的概率為1/8，r小於1的概率為1/16。1/16正好是maxLevel層插入元素的概率，1/8正好是maxLevel層插入的概率，以此類推。

通過這樣的分析，我們可以先比較r和1，如果r<1，那麼元素就要插入到maxLevel層以下；否則再比較r和2，如果r<2，那麼元素就要插入到maxLevel-1層以下；再比較r和4，如果r<4，那麼元素就要插入到maxLevel-2層以下……如果r>2^(maxLevel - 1)，那麼元素就只要插入在底層即可。

以上分析是隨機數演算法的關鍵。演算法跟實現跟語言無關，但是Java程式設計師還是更容易看明白Java程式碼實現的跳躍表，以下貼一下別人的java程式碼實現。作者找不到了，就這樣吧。

 1 /***************************  SkipList.java  *********************/
 2 
 3 import java.util.Random;
 4 
 5 public class SkipList<T extends Comparable<? super T>> {
 6     private int maxLevel;
 7     private SkipListNode<T>[] root;
 8     private int[] powers;
 9     private Random rd = new Random();
10     SkipList() {
11         this(4);
12     }
13     SkipList(int i) {
14         maxLevel = i;
15         root = new SkipListNode[maxLevel];
16         powers = new int[maxLevel];
17         for (int j = 0; j < maxLevel; j++)
18             root[j] = null;
19         choosePowers();
20     }
21     public boolean isEmpty() {
22         return root[0] == null;
23     }
24     public void choosePowers() {
25         powers[maxLevel-1] = (2 << (maxLevel-1)) - 1;    // 2^maxLevel - 1
26         for (int i = maxLevel - 2, j = 0; i >= 0; i--, j++)
27            powers[i] = powers[i+1] - (2 << j);           // 2^(j+1)
28     }
29     public int chooseLevel() {
30         int i, r = Math.abs(rd.nextInt()) % powers[maxLevel-1] + 1;
31         for (i = 1; i < maxLevel; i++)
32             if (r < powers[i])
33                 return i-1; // return a level < the highest level;
34         return i-1;         // return the highest level;
35     }
36     // make sure (with isEmpty()) that search() is called for a nonempty list;
37     public T search(T key) { 
38         int lvl;
39         SkipListNode<T> prev, curr;            // find the highest nonnull
40         for (lvl = maxLevel-1; lvl >= 0 && root[lvl] == null; lvl--); // level;
41         prev = curr = root[lvl];
42         while (true) {
43             if (key.equals(curr.key))          // success if equal;
44                  return curr.key;
45             else if (key.compareTo(curr.key) < 0) { // if smaller, go down,
46                  if (lvl == 0)                 // if possible
47                       return null;      
48                  else if (curr == root[lvl])   // by one level
49                       curr = root[--lvl];      // starting from the
50                  else curr = prev.next[--lvl]; // predecessor which
51             }                                  // can be the root;
52             else {                             // if greater,
53                  prev = curr;                  // go to the next
54                  if (curr.next[lvl] != null)   // non-null node
55                       curr = curr.next[lvl];   // on the same level
56                  else {                        // or to a list on a lower level;
57                       for (lvl--; lvl >= 0 && curr.next[lvl] == null; lvl--);
58                       if (lvl >= 0)
59                            curr = curr.next[lvl];
60                       else return null;
61                  }
62             }
63         }
64     }
65     public void insert(T key) {
66         SkipListNode<T>[] curr = new SkipListNode[maxLevel];
67         SkipListNode<T>[] prev = new SkipListNode[maxLevel];
68         SkipListNode<T> newNode;
69         int lvl, i;
70         curr[maxLevel-1] = root[maxLevel-1];
71         prev[maxLevel-1] = null;
72         for (lvl = maxLevel - 1; lvl >= 0; lvl--) {
73             while (curr[lvl] != null && curr[lvl].key.compareTo(key) < 0) { 
74                 prev[lvl] = curr[lvl];           // go to the next
75                 curr[lvl] = curr[lvl].next[lvl]; // if smaller;
76             }
77             if (curr[lvl] != null && key.equals(curr[lvl].key)) // don't 
78                 return;                          // include duplicates;
79             if (lvl > 0)                         // go one level down
80                 if (prev[lvl] == null) {         // if not the lowest
81                       curr[lvl-1] = root[lvl-1]; // level, using a link
82                       prev[lvl-1] = null;        // either from the root
83                 }
84                 else {                           // or from the predecessor;
85                      curr[lvl-1] = prev[lvl].next[lvl-1];
86                      prev[lvl-1] = prev[lvl];
87                 }
88         }
89         lvl = chooseLevel();                // generate randomly level 
90         newNode = new SkipListNode<T>(key,lvl+1); // for newNode;
91         for (i = 0; i <= lvl; i++) {        // initialize next fields of
92             newNode.next[i] = curr[i];      // newNode and reset to newNode
93             if (prev[i] == null)            // either fields of the root
94                  root[i] = newNode;         // or next fields of newNode's
95             else prev[i].next[i] = newNode; // predecessors;
96         }
97     }
98 }