演算法筆記_082:藍橋杯練習 12-1三角形（Java）

weixin_33896726發表於2017-03-16
演算法筆記Java

目錄

1 問題描述

2 解決方案

 

1 問題描述

問題描述
　　為二維空間中的點設計一個結構體，在此基礎上為三角形設計一個結構體。分別設計獨立的函式計算三角形的周長、面積、中心和重心。輸入三個點，輸出這三個點構成的三角形的周長、面積、外心和重心。結果保留小數點後2位數字。
樣例輸出
與上面的樣例輸入對應的輸出。
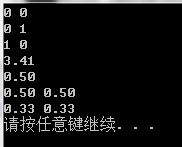
例：
資料規模和約定
　　輸入資料中每一個數的範圍。
　　例：doule型表示資料。

 

2 解決方案

本題主要考查三角形相關數學知識，剛開始做的時候，我對重心和外心的計算公式一點都記不起來，無語中...，後來，計算外心的時候，也出錯，因為沒有單獨劃分出橫座標相等的情況，導致計算出錯。

 

具體程式碼如下：

import java.util.Scanner;

public class Main {
    
    //計算三角形三條邊的長
    public double[] getABC(double[][] point) {
        double[] edge = new double[3];
        double x1 = point[0][0], y1 = point[0][1];
        double x2 = point[1][0], y2 = point[1][1];
        double x3 = point[2][0], y3 = point[2][1];
        edge[0] = (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2);
        edge[0] = Math.sqrt(edge[0]);
        edge[1] = (x1 - x3) * (x1 - x3) + (y1 - y3) * (y1 - y3);
        edge[1] = Math.sqrt(edge[1]);
        edge[2] = (x2 - x3) * (x2 - x3) + (y2 - y3) * (y2 - y3);
        edge[2] = Math.sqrt(edge[2]);
        return edge;
    }
    
    //計算三角形的周長
    public double getL(double[][] point) {
        double[] edge = getABC(point);
        return edge[0] + edge[1] + edge[2];
    }
    
    //計算三角形的面積
    public double getS(double[][] point) {
        double[] edge = getABC(point);
        double p = (edge[0] + edge[1] + edge[2]) / 2;
        double S = p * (p - edge[0]) * (p - edge[1]) * (p - edge[2]);  //海倫公式
        S = Math.sqrt(S);
        return S;
    }
    
    //計算三角形的外心（PS：三角形外接圓的圓心，外心到三個頂點距離相等）
    public double[] getExcenter(double[][] point) {
        double[] center = new double[2];
        double x1 = point[0][0], y1 = point[0][1];
        double x2 = point[1][0], y2 = point[1][1];
        double x3 = point[2][0], y3 = point[2][1];
        double a , b , c , d ;
           a = (x1*x1 + y1*y1 - x2*x2 - y2*y2) * (x1 - x3) / 2;
           b = (x1*x1 + y1*y1 - x3*x3 - y3* y3) * (x1 - x2) / 2;
           c = (y1 - y2) * (x1 - x3);
           d = (y1 - y3) * (x1 - x2);
        center[1] = (a - b) / (c - d);  //外心的縱座標
        double e, f;
        if(x1 != x2) {   //防止出現兩點的橫座標相等的情況
            e = (x1*x1 + y1*y1 - x2*x2 - y2*y2) / (2 * (x1 - x2));
            f = (y1 - y2) / (x1 - x2);
            center[0] = e - f * center[1];  //外心的橫座標
        } else if(x1 != x3) {
            e = (x1*x1 + y1*y1 - x3*x3 - y3*y3) / (2 * (x1 - x3));
            f = (y1 - y3) / (x1 - x3);
            center[0] = e - f * center[1];
        } else if(x2 != x3) {
            e = (x2*x2 + y2*y2 - x3*x3 - y3*y3) / (2 * (x2 - x3));
            f = (y2 - y3) / (x2 - x3);
            center[0] = e - f * center[1];
        }
        return center;  
    }
    
    //計算三角形的重心（PS：三角形中三條邊的中線交點）
    public double[] getBarycenter(double[][] point) {
        double[] center = new double[2];
        double x1 = point[0][0], y1 = point[0][1];
        double x2 = point[1][0], y2 = point[1][1];
        double x3 = point[2][0], y3 = point[2][1];
        center[0] = (x1 + x2 + x3) / 3;  //重心的橫座標
        center[1] = (y1 + y2 + y3) / 3;  //重心的縱座標
        return center;
    }
    
    //輸出題意結果
    public void printResult(double[][] point) {
        double L = getL(point);
        double S = getS(point);
        double[] exCenter = getExcenter(point);
        double[] baryCenter = getBarycenter(point);
        System.out.printf("%.2f\n",L);
        System.out.printf("%.2f\n",S);
        System.out.printf("%.2f",exCenter[0]);
        System.out.printf(" %.2f\n",exCenter[1]);
        System.out.printf("%.2f",baryCenter[0]);
        System.out.printf(" %.2f\n",baryCenter[1]);
        
    }
    
    public static void main(String[] args) {
        Main test = new Main();
        Scanner in = new Scanner(System.in);
        double[][] point = new double[3][2];
        for(int i = 0;i < 3;i++) {
            point[i][0] = in.nextDouble();
            point[i][1] = in.nextDouble();
        }
        test.printResult(point);
    }
}

 

相關文章