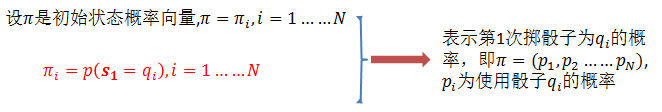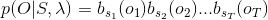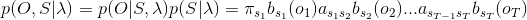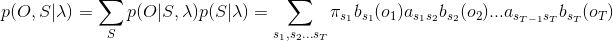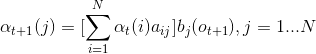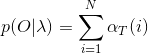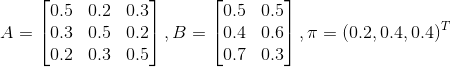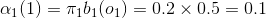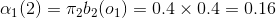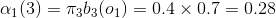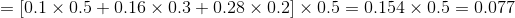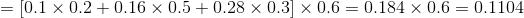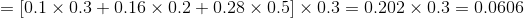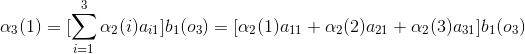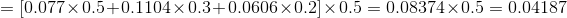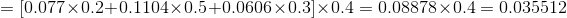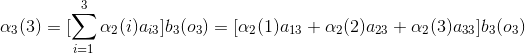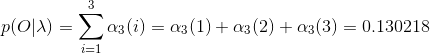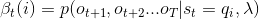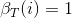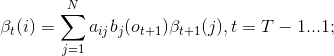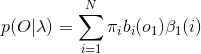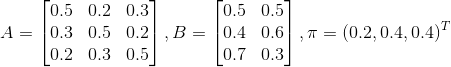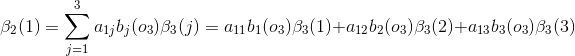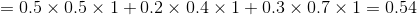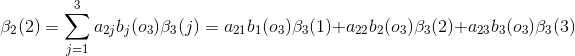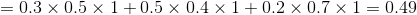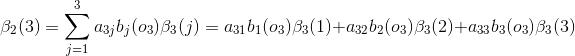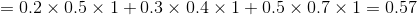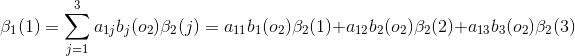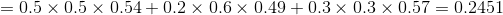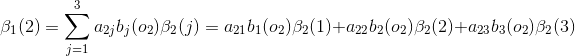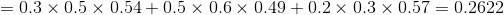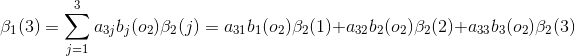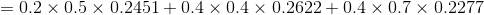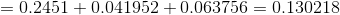隱馬爾科夫模型前向後向演算法
本文是自己學習隱馬爾科夫模型的一個總結,為了自己以後方便查閱,也算作是李航老師的《統計學習方法》的一個總結,若有疑問,歡迎討論。
推薦閱讀知乎上Yang Eninala寫的《如何用簡單易懂的例子解釋隱馬爾可夫模型?》,寫的非常好。我會聯絡兩者,來作為自己的一篇學習筆記。
隱馬爾可夫模型: 隱馬爾可夫模型是關於時序的概率模型,描述由一個隱藏的馬爾可夫鏈隨機生成不可觀測的狀態隨機序列,再由各個狀態生成一個觀測而產生觀測隨機序列的過程。隱藏的馬爾可夫鏈隨機生成的狀態的序列,稱為狀態序列(state sequence),每個狀態生成一個觀測,而由此產生的觀測的隨機序列,稱為觀測序列(observation sequenoe )。序列的每一個位置又可以看作是一個時刻。
隱馬爾科夫模型的3個基本問題:
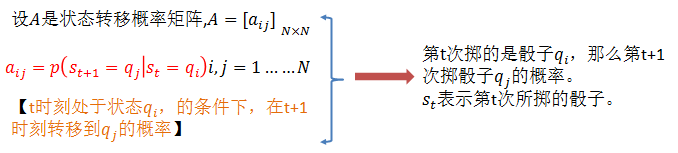
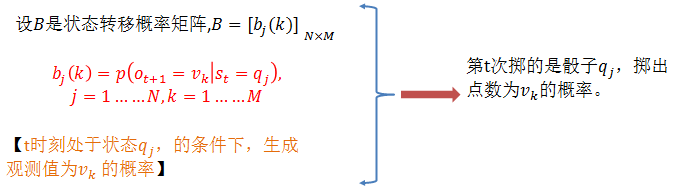
(1)概率計算問題。給定模型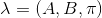
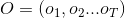
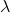
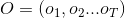
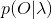
(2)學習問題。已知觀測序列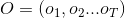
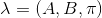
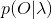
(3)預測問題,也稱為解碼(decoding)問題。已知模型引數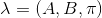
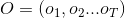
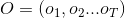
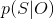
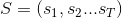
概率計算問題:
1、 直接計算方法
這種方法說白了就是暴力搜尋,列舉每一種狀態序列,然後在根據狀態序列求出觀測序列的概率。
思想很簡單,可以這麼想:假如我們現在已知狀態序列為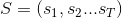

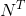
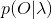
狀態序列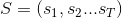
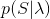
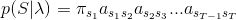
對已經假設的狀態序列
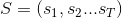 ,觀測序列
,觀測序列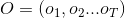 ,的概率是
,的概率是 :
:觀測序列O和狀態序列S同時出現的概率是:
最後,對所有的狀態序列S求和,即可得到觀測序列O的概率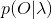
對於實現上式,很簡單,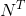
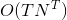
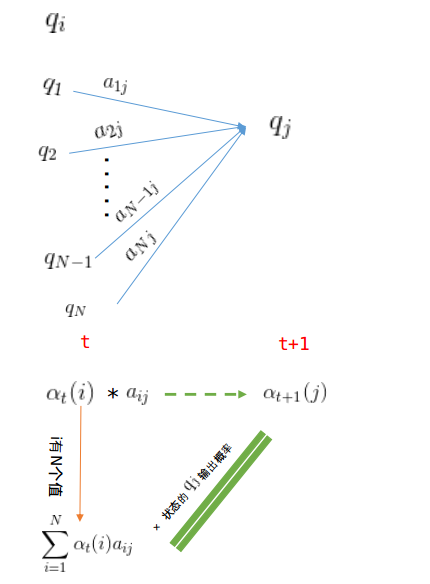
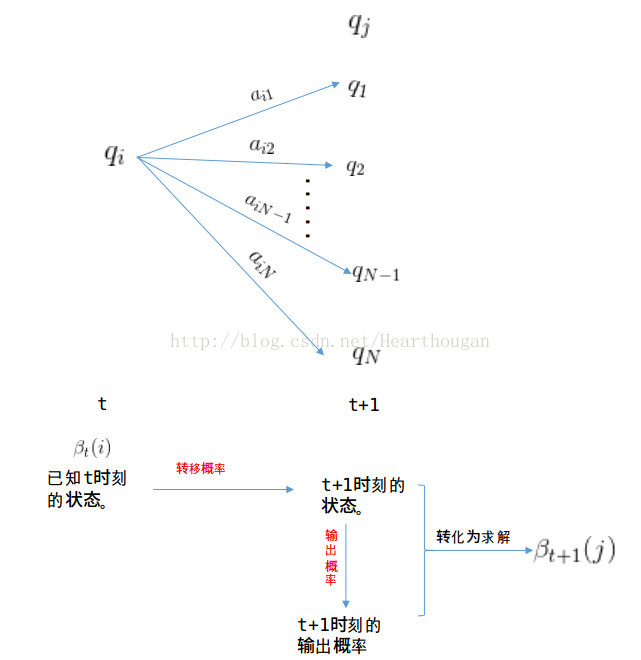
2、前向演算法:
給定隱馬爾可夫模型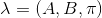
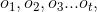
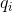
可以遞推地求得前向概率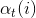
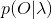
這個可以這麼理解,已知選每種骰子的概率,每種骰子的輸出概率,那麼前t次擲骰子,擲出的點數為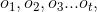
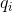
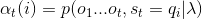
(1)初值:
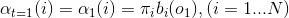
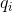 ,擲出的點數為
,擲出的點數為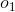 的概率,其中
的概率,其中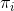 表示開始的時候選用骰子
表示開始的時候選用骰子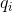 的概率】
的概率】(2)遞推:
【第t+1次用骰子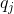
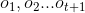
上式方括號中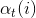
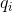
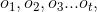
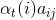
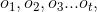
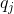
由於第t次骰子的種類有N種,因此,第t+1次使用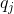
(3)終止:
根據(2)的遞推式子可以求出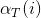
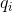
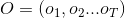
例子1(前向演算法):考慮盒子和球模型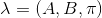
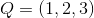
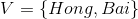
設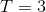
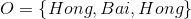
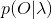
根據上面我們描述的演算法,一步一步地計算,
(1)計算初值:
(2)遞推:
當
當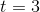
3、後向演算法
給定隱馬爾可夫模型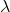
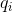
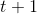
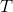
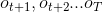
可以遞推地求得後向概率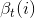
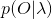
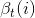
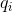
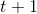
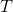

(1)初值
【解釋:已知最後一次所用的骰子為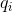
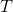
(2)遞推
(3)終止
後向演算法依舊是解決概率計算問題,只不過是兩種計算方式,計算結果應該是和前向演算法相同,可以用例1驗證一下,如下:
例2(後向演算法),考慮盒子和球模型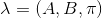

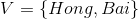
設

我們仍然根據上面的演算法描述,一步一步地計算,
(1)計算初值
當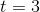
(2)遞推
當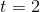
當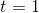
(3)終止
可以根絕前向演算法和後向演算法的定義,將兩種計算方式結合起來,如下:
相關文章
- 隱馬爾科夫模型HMM(二)前向後向演算法評估觀察序列概率馬爾科夫模型HMM演算法
- 【HMM】隱馬爾科夫模型HMM馬爾科夫模型
- 隱馬爾科夫模型HMM(一)HMM模型馬爾科夫模型HMM
- 隱馬爾科夫模型(HMM)分詞研究馬爾科夫模型HMM分詞
- 隱馬爾可夫模型隱馬爾可夫模型
- 用hmmlearn學習隱馬爾科夫模型HMMHMM馬爾科夫模型
- HMM隱馬爾可夫模型HMM隱馬爾可夫模型
- 隱馬爾可夫模型詳解隱馬爾可夫模型
- 10_隱馬爾可夫模型隱馬爾可夫模型
- ML-隱馬爾可夫模型隱馬爾可夫模型
- 機器學習之隱馬爾可夫模型機器學習隱馬爾可夫模型
- 隱馬爾可夫模型 | 賽爾筆記隱馬爾可夫模型筆記
- 隱馬爾科夫模型HMM(三)鮑姆-韋爾奇演算法求解HMM引數馬爾科夫模型HMM演算法
- 隱馬爾科夫模型HMM(四)維特比演算法解碼隱藏狀態序列馬爾科夫模型HMM維特比演算法
- 【機器學習】--隱含馬爾科夫模型從初識到應用機器學習馬爾科夫模型
- 隱馬爾可夫模型(HMM)詳解隱馬爾可夫模型HMM
- 隱馬爾可夫模型及應用隱馬爾可夫模型
- 隱馬爾可夫模型的Viterbi解碼演算法隱馬爾可夫模型Viterbi演算法
- 隱馬爾可夫模型(HMM)中文分詞隱馬爾可夫模型HMM中文分詞
- 一個隱馬爾科夫模型的應用例項:中文分詞馬爾科夫模型中文分詞
- 隱馬爾科夫模型python實現簡單拼音輸入法馬爾科夫模型Python
- 維特比演算法和隱馬爾可夫模型的解碼維特比演算法隱馬爾可夫模型
- 隱馬爾可夫模型(HMM)實現分詞隱馬爾可夫模型HMM分詞
- MCMC(二)馬爾科夫鏈馬爾科夫
- HMM隱馬爾可夫模型來龍去脈(二)HMM隱馬爾可夫模型
- NLP-隱馬爾可夫模型及使用例項隱馬爾可夫模型
- HMM-前向後向演算法HMM演算法
- 一個馬爾科夫鏈例項馬爾科夫
- 用簡單易懂的例子解釋隱馬爾可夫模型隱馬爾可夫模型
- 馬爾可夫鏈模型(轉載)馬爾可夫模型
- 2022-05-17-馬爾科夫鏈之傳統馬爾可夫鏈馬爾科夫馬爾可夫
- 馬爾科夫鏈的穩態分佈馬爾科夫
- 馬爾科夫鏈隨機文字生成器馬爾科夫隨機
- 【火爐煉AI】機器學習045-對股票資料進行隱馬爾科夫建模AI機器學習馬爾科夫
- 使用馬爾可夫模型自動生成文章馬爾可夫模型
- 域結構進化的馬爾可夫模型馬爾可夫模型
- CVPR 2021 | 時間序列疾病預測的因果隱馬爾可夫模型隱馬爾可夫模型
- R資料分析:縱向分類結局的分析-馬爾可夫多型模型的理解與實操馬爾可夫多型模型