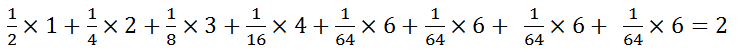如何理解用資訊熵來表示最短的平均編碼長度

       之前弄明白了資訊熵是什麼，由於資訊熵來源於資訊理論，要怎麼才能跟編碼聯絡起來呢？這個問題當時沒有想明白，今天查了一下資料，理解了一下，做筆記整理一下，如有錯誤歡迎指正。

如果資訊熵不明白的請看這裡：http://blog.csdn.net/hearthougan/article/details/76192381

首先給出結果：

最短的平均編碼長度 = 信源的不確定程度 / 傳輸的表達能力。

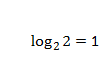
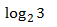
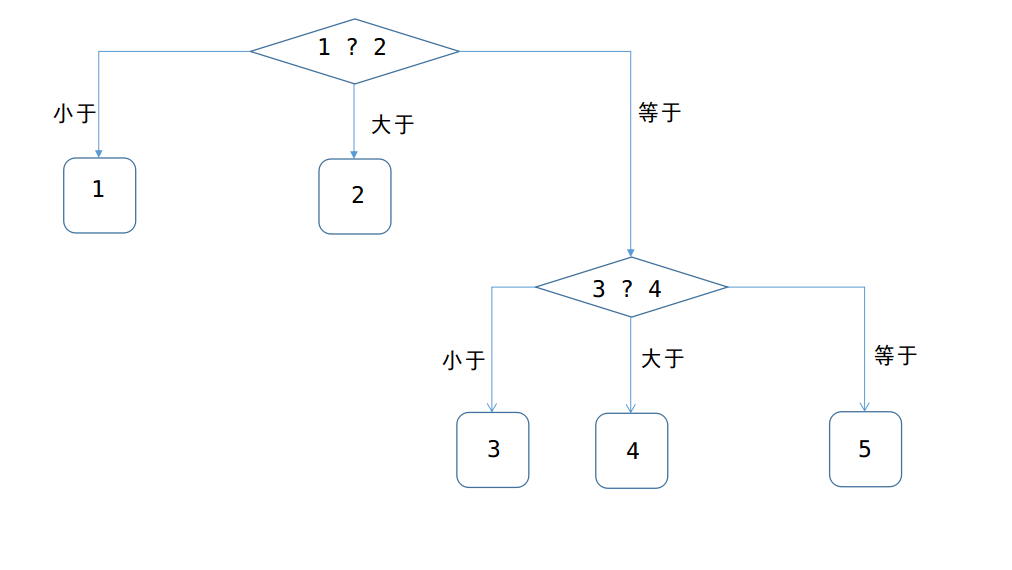
其中信源的不確定程度，用信源的熵來表示，又稱之為被表達者，傳輸的表達能力，稱之為表達者表達能力，如果傳輸時有兩種可能，那表達能力就是，如果是傳輸時有三種可能，那表達能力就是。以例子來描述，儘量做到通俗易懂。

例1：昨天小明錯過一場有8匹賽馬的比賽，編號為1~8號，每匹馬贏的概率都一樣，那麼作為朋友的你要把獲勝馬的編號傳送給他，那麼你該怎麼做？

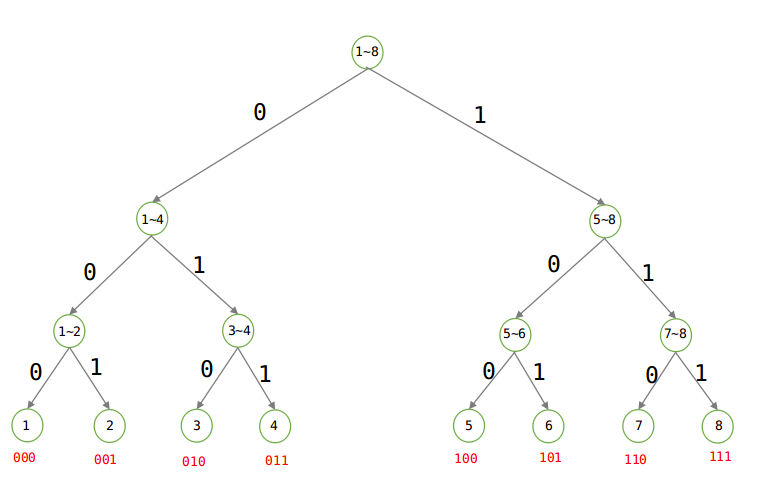
方法一：直接傳送馬的編號，這樣描述一匹馬需要3位元（000,001,010,011,100,101,110,111）。

方法二：利用資料結構中的Huffman編碼，如下：

建立Huffman樹：

由上圖可知，當等概率的時候，傳送資訊仍至少需要3位元。

被表達者：直接根據概率求熵即可，1/8×log8 * 8 = 3位元。

表達者：由圖可以看出來Huffman樹是一顆二叉樹，要麼是0，要麼是1，所以表達能力就是log2.

平均編碼長度 = 3/log2 = 3位元，注意其中的log 都是以2為底的。

例2：昨天小明錯過一場有8匹賽馬的比賽，編號為1~8號，1~8號獲勝的概率分別為{1/2、1/4、 1/8、 1/16、 1/64、 1/64、 1/64、 1/64}，那麼作為朋友的你要把獲勝馬的編號傳送給他，那麼你該怎麼做？

方法一：仍然直接傳送馬的編號，這樣描述一匹馬需要3位元（000,001,010,011,100,101,110,111）。

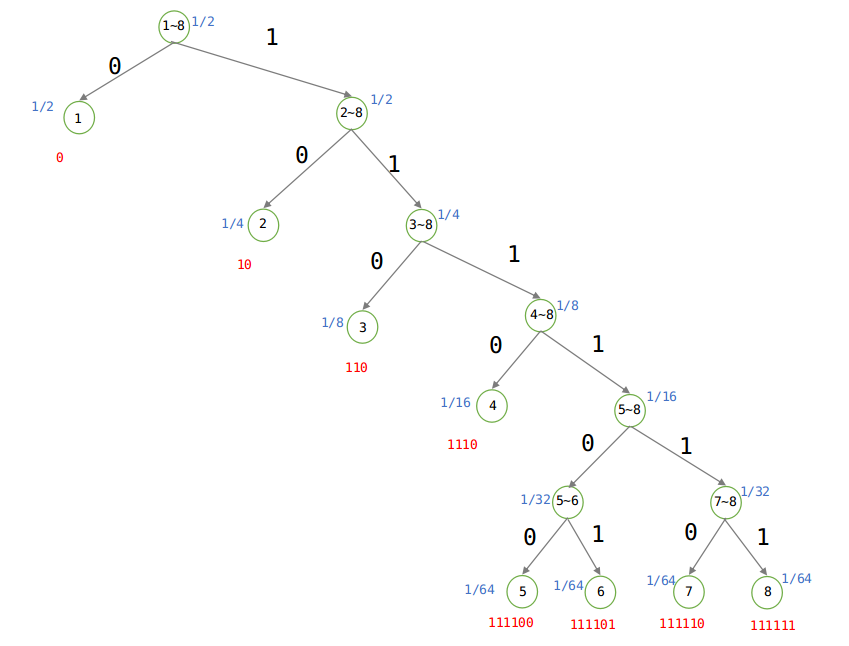
方法二：利用資料結構中的Huffman編碼，如下：

建立Huffman樹：

由於概率不相等，則根據Huffman樹可知平均編碼為：（1 × 1/2 + 2 × 1/4 + 3 × 1/8 + 4 × 1/16 + 6 × 1/64 + 6 × 1/64 + 6 × 1/64 + 6 × 1/64） = 2位元，當概率不相等的時候，傳送的平均長度為2位元。

由上圖可知：

被表達者（不確定程度）：

表達者：由圖可以看出來Huffman樹是一顆二叉樹，要麼是0，要麼是1，所以表達能力就是log2.

平均編碼長度：2/log2 = 2位元。

例3：假設有5個硬幣：1,2,3,4,5，其中一個是假的，比其他的硬幣輕。有一個天平，天平每次能比較兩堆硬幣，得出的結果可能是以下三種之一：
左邊比右邊輕
右邊比左邊輕
兩邊同樣重
問：至少要使用天平多少次才能保證找到假硬幣?

答案：是2次，

方法一：可作出如下圖的抉擇：

所以至少稱重2次，才可以確保找出。

方法二：

設X表示硬幣，Y表示天平，則，X的取值可以是5枚硬幣中的任意一枚，每個硬幣的概率都是1/5，那麼隨機變數X的不確定程度就是:

H(X) = 1/5×log5 + 1/5×log5 + 1/5×log5 + 1/5×log5 +1/5×log5 = log5

Y表示天平，A、B兩個硬幣放在天平，有三種情況：A < B, A > B, A = B。也就是說Y的表達能力就是log3.因此：

平均編碼長度: log5 / log3 = 1.46;換算成次數，也就是至少2次可以確保找到假硬幣！

例4、假設有5個硬幣：1,2,3,…5，其中一個是假的，比其他的硬幣輕。已知第一個硬幣是假硬幣的概率是三分之一；第二個硬幣是假硬幣的概率也是三分之一，其他硬幣是假硬幣的概率都是九分之一。
有一個天平，天平每次能比較兩堆硬幣，得出的結果可能是以下三種之一：
左邊比右邊輕
右邊比左邊輕
兩邊同樣重
假設使用天平n次找到假硬幣。問n的期望值至少是多少？

方法一：同樣利用Huffman編碼的思想，得出下圖：

       由上圖可以知道，至少稱重2次才可以找到假硬幣，這一題與上一題的差別就是，是每一枚硬幣的可能性都不一樣，所以先比較概率最大的兩枚1,2，找到假幣的概率佔了2/3，如果不在1 、2中，那麼從3~5中隨便取出兩枚硬幣，（上圖選取的是3 、4兩枚硬幣）再稱一次，就可以找打假硬幣！

方法二：

設X表示硬幣，Y表示天平，則，X的取值可以是5枚硬幣中的任意一枚，每個硬幣的概率分別是{1/3,1/3,1/9,1/9，1/9}，那麼隨機變數X的不確定程度就是:

H(X) = 1/3 * log3 + 1/3 * log3 + 1/9 *log9 + 1/9 *log9 + 1/9 *log9 = 4/3 *log3;

天平的表達能力同樣還是log3；

則平均編碼長度：4/3×log 3 / log 3 = 4/3,所以還是需要稱重兩次。

總結：

由上面4個例子，可以知道很清楚的知道，最短的平均編碼長度（也就是我們猜的次數，稱重的次數），是由隨機變數的熵，除以，表達能力的，得到！